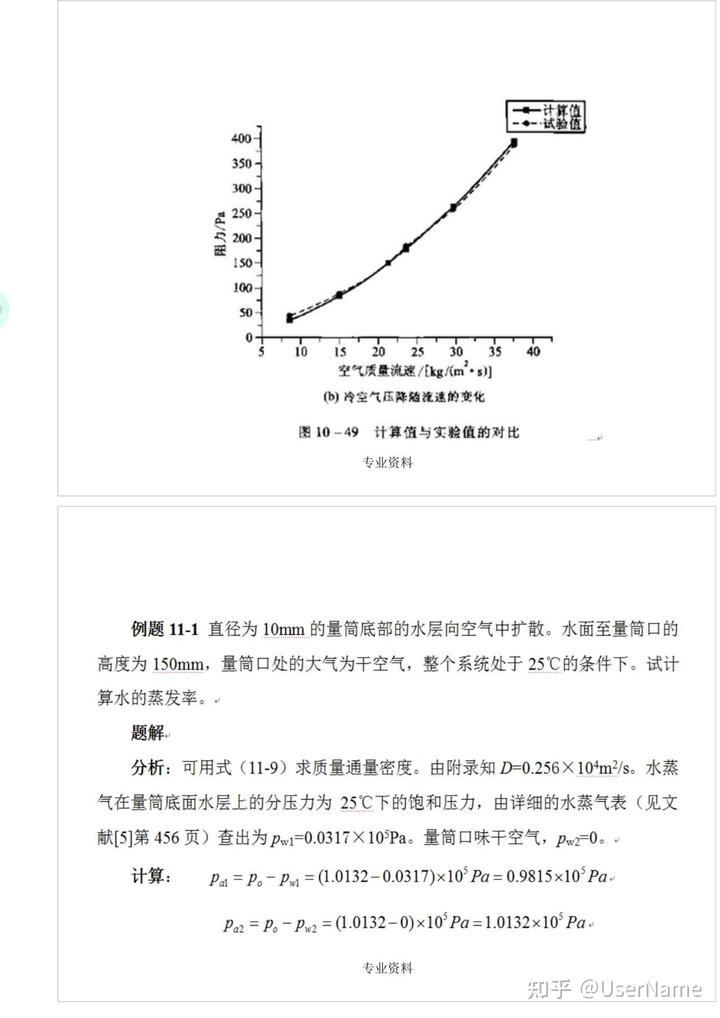
散熱量
傳熱學(第四版)例題專業資料討論:從上表可以看出從i=3這一時刻起出現了這樣的情況:個點溫度隨時間做忽高忽低的波動,并且波動弧度越來越
傳熱學(第四版)例題
專業資料



















































































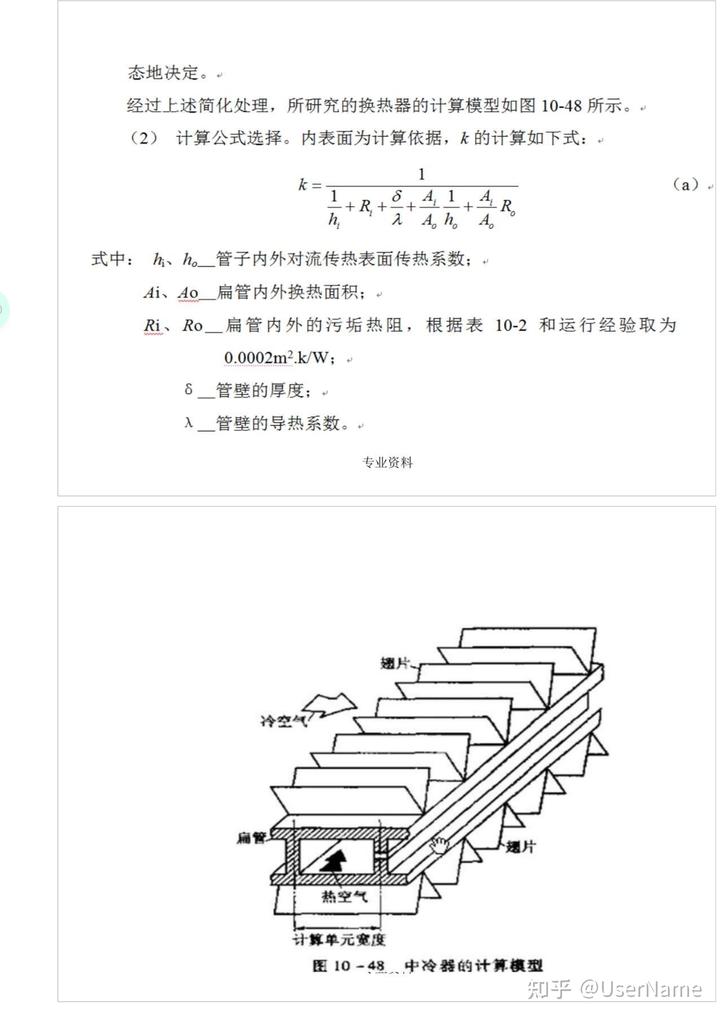









































討論:從上表可以看出從i=3這一時刻起出現了這樣的情況:個點溫度隨時間做忽高忽低的波動,并且波動弧度越來越大,某點溫度越高反使其相繼時刻的溫度越低,例>3
這種想象是荒謬的,它違反了熱力學第二定律,因為這意味著,在該時間間隔中從某一時刻起熱量將自動的由低溫點向高溫點傳遞。數值計算中出現這種計算結果忽高忽低的波動現象,數學上稱為不穩定性,這個例題表明,保證數值計算格式的穩定性是很重要的。
專業資料
例題4—4環肋肋效率計算用數值方法確定當r2/r=2,3,4
時環肋肋效率,其中r2,r1為環肋外半徑及根圓半徑(圖4—12a)
假設(1)流體的表面傳熱系數為常數(2)一維穩態導熱(3)肋片物性為常數(4)環肋頂端絕熱
分析這是圓柱坐標中常物性一維穩態導熱問題,導熱微分方程式2—12可化簡為
にボキー0 rdr dr
λ 將肋片上下表面的換熱量折算成內熱源:
Φ=2
(2πrdr)h(t-t,)
2
h(t-ty) (2πrdr)δ
8 t-tf Θ
引入無量綱過于溫度
to-tf 及無量綱半徑
R=
H
專業資料
可得這一導熱問題的數學描寫
d2Θ dΘ
-2㎡Θ=0 +
dR2 RdR R=R,Θ=1 R=R2,de
=0
dR 式中:
h 3/2
R1=r/H,R2=r2/H m=
x
VλA
由此可見,為了計算不同嚇得肋效率需以m為參數。
計算:式4—23a是圓柱坐標中的無量綱一維穩態導熱方程,式中的兩個導數項分別用相應的中心差分格式代入,可得以下的差分方程式
-n+1-2-n++n
1n+1n-12㎡+n=0 AR2
R,
2AR
n=1,2,3.....N-1,Θ1=1,Θn=Θn-1 上式是肋頂絕熱條件的一種數值處理方式
也可用高斯—賽德爾迭代法求解,獲得Θn后再按定義計算肋效率
專業資料
ZAe
>AA
式中ΔA;為任意節點i所代表的微元體的換熱表面積。,為該節點的無量綱過于溫度。
表4—2列出了節點數N對肋效率η的影響。由表可見,為使在三位有效數字下的解穩定,應取N=36,此時可以認為已獲得與網格無關的解。不同
肋效率隨 m的變化列于下表
節點數對肋效率的影響
2/r
=2,m=2) N
8
16 20 36 64
100 7
0.26357 0.27082 0.27149 0.27238 0.27244
0.27249 環肋肋效率隨
r2/r汲m的變化 0.1
0.5
1.0 1.5
2.0
2.5 2
0.991
0.813
0.542
0.37
0.272
0.213 3
0.989 0.781
0.490 0.321 0.23
0.177 4
0.987 0.756
0.454資料 0.29
0.204 0.154
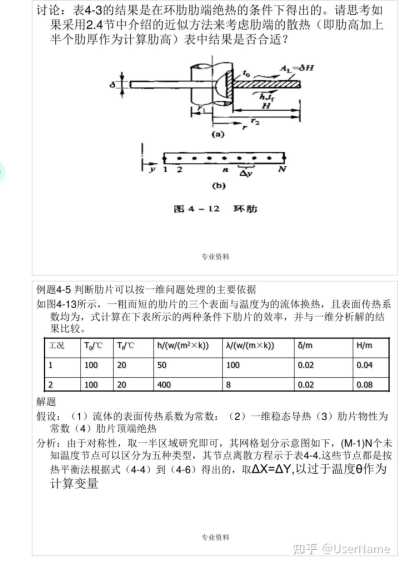
討論:表4—3的結果是在環肋肋端絕熱的條件下得出的。請思考如果采用2.4節中介紹的近似方法來考慮肋端的散熱(即肋高加上半個肋厚作為計算肋高)表中結果是否合適?
=δH (a)
: 2
(q) 圖4-12
環助
專業資料
例題4—5判斷肋片可以按一維問題處理的主要依據
如圖4—13所示,一粗而短的肋片的三個表面與溫度為的流體換熱,且表面傳熱系數均為,式計算在下表所示的兩種條件下肋片的效率,并與一維分析解的結果比較。
工況
T/℃
h/(w/(㎡2xk))
N/(w/(mxk))
δ/m
H/m 0./1
1 100 20 50
100
0.02
0.04 2
100 20 400
8
0.02
0.08 解題
假設:(1)流體的表面傳熱系數為常數:(2)一維穩態導熱(3)肋片物性為常數(4)肋片頂端絕熱
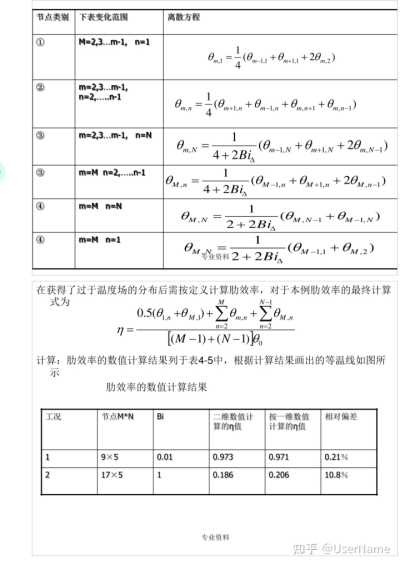
分析:由于對稱性,取一半區域研究即可,其網格劃分示意圖如下,(M—1)N個未知溫度節點可以區分為五種類型,其節點離散方程示于表4—4.這些節點都是按熱平衡法根據式(4—4)到(4—6)得出的,取ΔX=ΔY,以過于溫度θ作為計算變量
專業資料
節點類別
下表變化范圍
離散方程 ①
M=2,3...m-1, n=1
(θm-1.1 +0m+l.
+20m.2) 1
θ = - 三
4 ②
n=2,.....n-1 m=2,3...m-1,
1 (θm+h.n
0m-1.n
0m.n+l
0m.n-1) -=
+
+
+ θ
4 ③
m=2,3...m-1,n=N
0mN
(θm-1,N 1
0m+l.N +
20 +
m,N-1 4+
2Bi
Λ ③
m=M n=2,.....n-1
θM.n
(θM-1,n 1
0M+1,n
20M.n-1) +
+ 4+
2Bi
7 ④
m=M n=N
OM.N
(θM,N-1
+OM-1,N) 1
2+2Bi ④
m=M n=1
θM
(OM-1.1+OM.2) 1
1 專業資料
2+2Bi
D
在獲得了過于溫度場的分布后需按定義計算肋效率,對于本例肋效率的最終計算式為
Σ +
Σ M
I-N θ
θ 0.5(01.n+θM.)+
M,n m,n
n=2
n=2 n
[(M-1)+(N-1)]θ。
計算:肋效率的數值計算結果列于表4—5中,根據計算結果畫出的等溫線如圖所示
肋效率的數值計算結果節點M*N
Bi
二維數值計
計算的η值 按一維數值
相對偏差 工況
算的η值 1
9x5
0.206
10.8% 0.01
0.973
0.971
0.21% 2
17x5
1
0.186 專業資料
對流
對流 28
H
④b
M h,fr
1 2 m
絕熱 圖4—13 粗而短的肋片的分析
圖4-14
例題4—5的網格劃分0/00=1
(a)工況1(Bi-0.01) 0/00=1
(b)工況2(Bi-1.0) 圖4-15
兩種肋片的等溫線圖
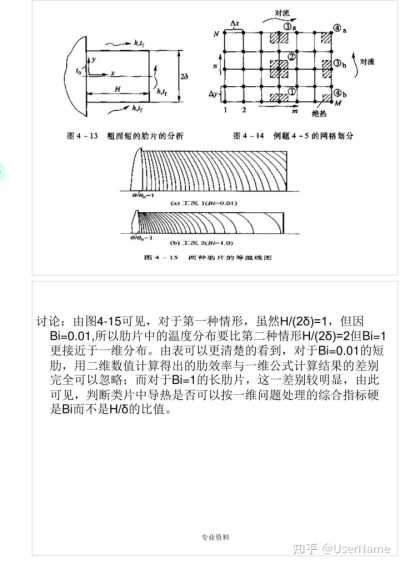
討論:由圖4—15可見,對于第一種情形,雖然H/(2δ)=1,但因
Bi=0.01,所以肋片中的溫度分布要比第二種情形H/(2δ)=2但Bi=1更接近于一維分布。由表可以更清楚的看到,對于Bi=0.01的短肋,用二維數值計算得出的肋效率與一維公式計算結果的差別完全可以忽略;而對于Bi=1的長肋片,這一差別較明顯,由此可見,判斷類片中導熱是否可以按一維問題處理的綜合指標硬是Bi而不是H/δ的比值。
專業資料
例題4—6平板非穩態過程中的溫度分布
用數值方法計算單側受熱的無限大平板的瞬態溫度場。平板厚δ=0.1m
初始溫度80℃,平板一側被溫度300℃的流體加熱,另一側絕熱。設表面傳熱系數h=1163W/(㎡.K),材料的,λ=50w/(m·k)a=1,39x10-5㎡/s
題解
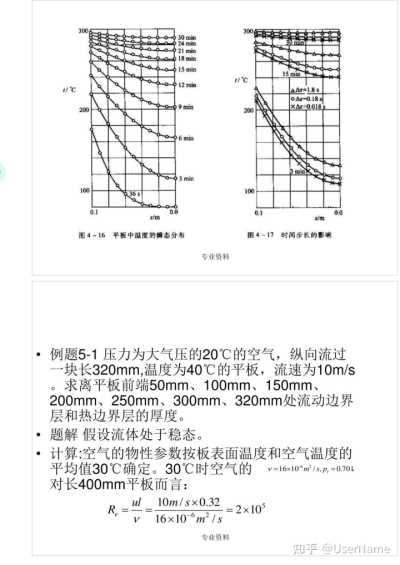
分析:這一問題可看作是厚度為28的平板兩側同時受流體加熱的第三類邊界條件下的非穩態導熱問題,其控制方程式為式(3—14)—(3—16).將平板10等分,共11個節點,節點離散方程如式(4—17)—(4—20)所示(節點編號方法見圖4—10)。計算計算結果采用等溫線來表示。幾個不同時刻平板中的溫度分布示于圖4—16.時間步長不同對計算結果的影響示于圖4—17.圖4—16的結果是按Δ,=0.18s
計算 得到的。
討論(1)由圖4—16可見,在
τ≤36s
的時間內,雖然平板受熱側已發生了顯著的溫度變化,但其絕熱側尚未受到界面上發生的熱擾動的影響,因而在這一段時間內把厚=0.2m
的平板當做半無限大物體來處理應是一種合理的處理應是一種合理的處理方法。實際上,對于a=1.39x103㎡/s 半厚度為0.1m的半個平板,根據3.5節的討論得其惰性時間為45s。
當t≥3min 后可以發現,平板中各點的溫度有規則的隨時間而上升,這就是非穩態導熱的正規狀態階段。實際上,=3min
時已有 at
1.39x103㎡/sx180s F0=
82
專業(0.1m)
=0.25
·(3)圖4—17表明,非穩態導熱計算中的瞬時溫度分布與時間步長的取值有關,但三種不同時間步長下解的差別在不斷縮小。兼顧到計算的準確度與計算的工作量兩方面的因素,本題以Aτ=0.18s
作為 計算步長。
專業資料
300
30min 24min
21 min
18min 15 min
15 min 0.
12 min t/℃
ΔΔr=1.8s
oΔr-0.18s 200
9 min
200
xΔ+=0.018s 6min
-0 3 min 001
100 00
0.1
0.0
0.1
0.0 x/m
w/x 圖4—16 平板中溫度的瞬態分布
圖4-17
時間步長的影響 專業資料
·例題5—1壓力為大氣壓的20℃的空氣,縱向流過一塊長320mm,溫度為40℃的平板,流速為10m/s。求離平板前端50mm、100mm、150mm、
200mm、250mm、300mm、320mm處流動邊界 層和熱邊界層的厚度。
·題解 假設流體處于穩態。
·計算:空氣的物性參數按板表面溫度和空氣溫度的平均值30℃確定。30℃時空氣的
v=16x10°㎡/s,p,=0.701 對長400mm平板而言:
ul
10m/sx0.32 R
=2x105 v
16x10-6㎡/s 專業資料
這Re數位于層流范圍內。其流動邊界層厚度按式(5—19)計算為
π2=5.0x 16x106㎡/s
x=6.36x10-3mx δ=5.0
10m/s 熱邊界層厚度可按式(5—21)計算:
δ
0
=1.138 0.701 d
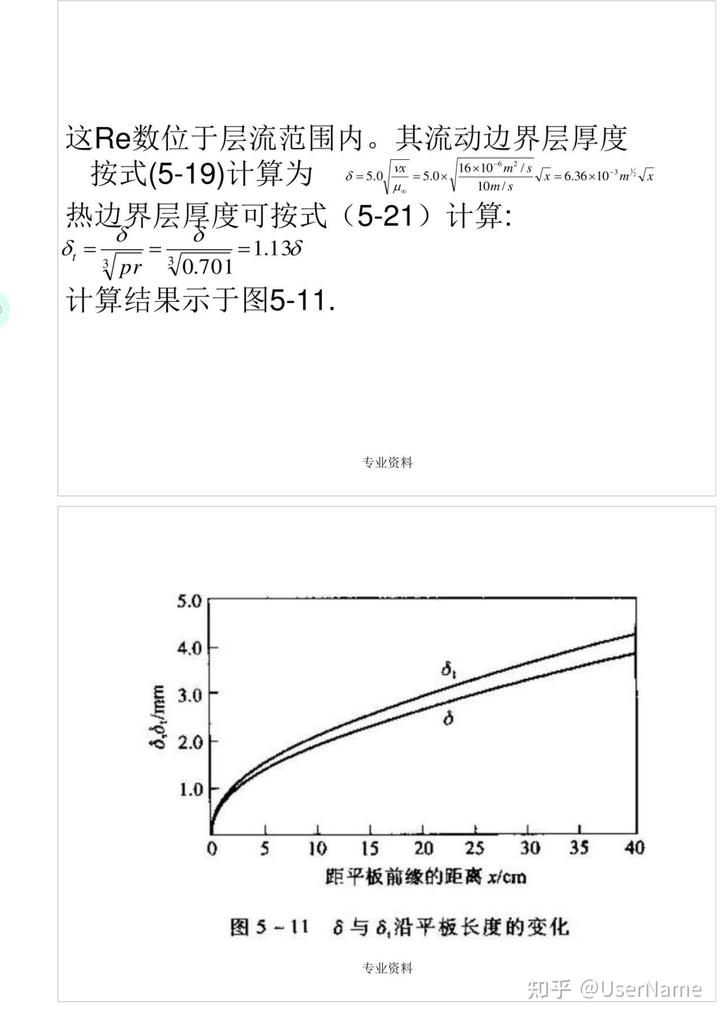
計算結果示于圖5—11.
專業資料 5.0
4.0
δ; 3.0
Q 2.0
1.0
T 0 5 10 15 20 25 30 35
40 距平板前緣的距離x/cm
圖5—11 δ與δ,沿平板長度的變化
專業資料
8,8,/mnm
例題5—2上例中,如平板的寬度為1m,求平板與空氣的換熱量。
題解
假設(1)穩態;(2)不計平板的輻射散熱。計算:先求平板的表面傳熱系數:
Nu=0.664RePr=0.664(2.0x10)2x0.701=263.7 λ
2.67x102w/(m·k)
x263.7=22.0w/(㎡·k) h=-Nu=
0.32m 1
式中
λ=2.67x102W/(m·K)
專業資料
是30℃時空氣的導熱系數。平板與空氣的換熱量為
Φ=hAΔt=22.0W/(㎡·K)x1mx0.32mx(40C-20°C)=140.8W
例題5—3離心力場作用下多孔介質物料層中的強制對流傳熱。如圖5—13所示,溫度為tf,in
流速為U
的流體,流經溫度均勻的固體顆粒層,顆粒層厚度為L,溫度為,t,>tf,in ,流體出口溫度為ut
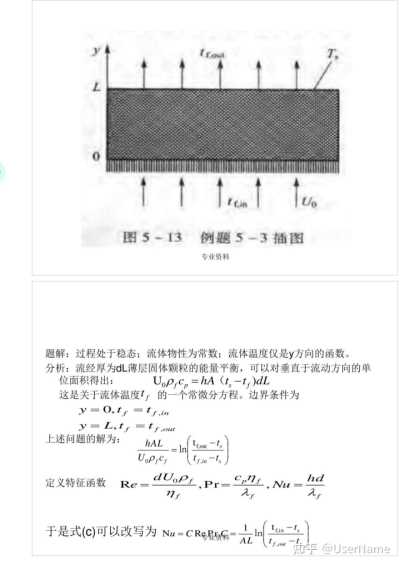
單位體積中的顆粒表面積為A,顆粒平均直徑為d。試據能量平衡導出流體與顆粒間的平均表面傳熱系數h和流體的速度、熱物理性質之間的關系式。
專業資料
7
0
Tuo ILin
圖5-13
例題5-3插圖 專業資料
題解:過程處于穩態;流體物性為常數;流體溫度僅是y方向的函數。
分析:流經厚為dL薄層固體顆粒的能量平衡,可以對垂直于流動方向的單位面積得出:
UoPfCp=hA(ts-t,)dL
這是關于流體溫度tf的一個常微分方程。邊界條件為y=O,tf=tf,in
y=L,tf=tf.out 上述問題的解為:
hAL
trout-ts In UoPfCf
tf.in-ts
hd dUoP1,Pr=
cpn1,Nu=
λf 定義特征函數
Re
x nf
于是式(c)可以改寫為
Nu=CRe=
1 trin u AL
例題5—4魚雷表面溫度的估計。
如圖所示一魚雷在10℃的海水中以15.4m/s的速度前進,受到的海水阻力為450N。假設魚雷內的電子器件耗功為50kw,試確定魚雷表面的平均溫度。
計算:
魚雷的表面積為
A=πdL=3.14x0.5mx5m=7.85㎡ 切應力為:
450N
=57.3N/㎡=57.3Pa 7.85㎡
10℃水的物性參數為Cp=4191J/(kg.K),Pr=9.52.有Chilton-Colburn公式可 得
h=
TCp57.3px419U/kg.K
=3480W/(㎡.k) UPr
15.4m/sx(9.52)■
魚雷的平均表面溫度可按生頓冷卻公式計算:
Φ
50000V
+10℃=1.8℃+10℃=11.8C hA
3480W/㎡.kx7.85m
專業資料 彈頭
燃料段
彈體尾部
尾部 50cm
6m
圖5—14 例題5—4圖示專業資料
例題5—5滾珠軸承中潤滑油摩擦生熱量的估算。
如圖5—15所示,一滾珠軸承用高粘度的油來潤滑。其中內圈運動,外圈靜止。已知內外圈的速度差為1m/s,內外圈的間距為1mm。潤滑油的動力粘度η=0.366Pa/s.試估算潤滑油中由于摩擦而產生的熱量。
假設:(1)潤滑油為牛頓流體(2)軸承環形間隙中的流體可以按平行板間隙中的流動來近似處理如圖(b)所示;(3)穩態過程。
計算:
=0.366P/sx
1m/s
=3.66x10W/m3 u=①
{m }
(?)4=(
0.001m 專業資料
內圈(轉動) 潤滑油
外圈(靜止)
滾珠 (日)
滾珠(轉動) 潤滑油 L-
(b) 0- 0 Δu
外圈(靜止)
圖5—15 滾珠軸承中流體運動的簡化模型
例題6-1
一換熱設備的工作條件是:壁溫 =80C 加熱=80C
的空氣 空氣流速u=0.5m/s。
采用一個全盤縮小成原設備1/5的模型來研究它的換熱情況。在模型中亦對空氣加熱,空氣溫度0C
壁面溫度℃
試問模型中流速u'應為多大才能保證與原設備中的換熱現象相似。題解:假設(1)穩態過程(2)被加熱物體以80℃計算其物性,模擬氣體以10℃計算其物性
計算:
非ー非 從而:
μ=/
取定性溫度為流體溫度與壁面溫度的平均值t=(t+t,)/2
從附 錄
v=23.13x106㎡/s,v=15.06x106㎡/s 查得
已知I/P'=5,于是模型中要求的流體速度u'為:
vl'(
0.5m/sx15.06x10㎡2/sx5 μ=μ
=1.63m/s 23.1Bx10-6㎡/s
1.4
例題6—2 用平均溫度為50℃的空氣來模擬平均溫度為400℃的煙氣的外掠管束的對流傳熱,模型中煙氣流速在10—15m/s范圍內變化。模擬采用與實物一樣的管徑,問模型中空氣的流速應在多大范圍內變化?假設:(1)穩態過程;(2)以50℃計算模擬氣體(空氣)的物性,以400℃計算實際工作氣體(煙氣)的物性。
計算:由附錄知:400℃的煙氣的
v=60.38x106㎡/s 50℃空氣的95x106㎡/s
·為使模型與實物中Re數的變化范圍相同,模型中空氣流速應為
17.95x106㎡/s
x(10-15)m/s=(2.94~4.46)m/s 60.38x106㎡/s
·安排實驗時模型中的空氣流速應在這一范圍內。
專業資料
例題6—3 水流過長l=5m、壁溫均勻的直管時,
從
y=25.3℃
被加熱到4.6℃ 管子的內徑d=20mm,水在管內的流速為2/s,求表面傳熱系數。
計算:水的平均溫度為
tj+t}
25.3℃+34.6C
=30℃ /1
2
2
以此為定性溫度,從附錄查的λ=0.618W/(m·K),v=0.805x10㎡/s,Pr,=5.42由此得
Re
2m/sx0.02m
4.97x10+>10 pr
Vf
0.805x106㎡/s
流動處于旺盛湍流區。采用式(6—15)求
Nu=0.023Re
0.8 Pr 0.4
=0.023x(4.97x10+)08x5.4204=258.5 )
M Nu=
0.618W/(m·K)
258.5=7988V/(m·K) x
d
0.02m
專業資料
·被加熱水每秒鐘的吸熱量為
πd -rd=Φ
cp(t-t,) /
=995.7kg/m3x2m/sx
3.14x(0.02m)2
x4174//(kg·K)x(34.6℃-25.3℃) 4
=2.43x104W 先用下式計算壁溫:
Φ tw=t+ hA
2.43x10+W =30℃+
℃=39.7
7988V/(㎡·K)x0.02mx3.14x5m
溫差遠小于20℃,在式(6—15)的適用范圍,所求結果即為本題答案。
專業資料
·例題6—4在低風洞中用電加熱圓管的方法來進行空氣橫掠水平放置圓管的對流換熱實驗。試驗管置于風洞的兩個側壁上,暴漏在空氣中的部分長100mm,外徑為12mm.實驗測得來流的t=15C 換熱表面平均溫度tw=125℃ ,功率P=40.5W.由于換熱管表面的輻射及換熱管兩端通過風洞側壁的導熱,估計有15%的功率損失,使計算此時對流傳熱的表面傳熱系數。
Φ 計算:由牛頓冷卻公式
h=
A(tw-t) 由已知得
Φ=0.58P=0.85x40.5W=34.43W 又
A=πdl=3.14x0.012mx0.1m=3.768x10-3㎡ 代入上式得
34.43W h
=83.1W(㎡·K) 3.768x10-3㎡x(125-15)℃
專業資料
例題 6—5 在一鍋爐中,煙氣橫掠4排管組成的順排管束。已知管外徑d=60mms/d=2,S2/d=2,煙氣平均溫度tf=600°C,tw=120°C。 煙氣通道最窄處平均流速u=8m/s。試求管束平均表面傳熱系數。
題解
分析:本題是直接給出了為采用茹卡烏斯卡斯公式所需的一切參數,可采用書末附表中平均煙氣成分的物性進行計算。
專業資料
計算:
由書末查得
Pr}=0.62,Pr=0.686v=93.61x106㎡/s,λ=7.42x102W/(m.k)
·又
Re=
8m/sx0.06m
=5128
93.61x10-6㎡/s
·按表6—7中的關聯式(6—31c)Nu,=0.27Re
0.63 P136 (Pr,/Pr)
0.25 f
=0.27x512863x0.620.36x
(0.62/0.686)025=48.2 λ
h=Nu=48.2x7.42x10-2w/(m·k)/0.06mm=59.6W/(㎡.k) d
·按表6—9,管排修正系數εn=0.91,故平均表面傳熱系數為h=Nu=59.6W/(㎡k)x0.91=54.2W/(㎡k)
專業資料
討論:(1)與管內對流傳熱存在多個關聯式的情形相類似,流體外掠管束也有不同的關聯式,對同一個問題的計算結果相互間也有一定的差異。例如Grimson公式就是另外一個關聯式(30,由于該式對一系列不同的S1、S2之值用表格方式給出了關聯式的指數與系數,使用不便,同時僅適用于氣體,因此本書不在推薦。
(2)作為例題,直接給出了為采用關聯式所需的條件。但在工程實際中測定換熱管子表面的平均溫度是很困難的。
比較接近實際應用條件的計算模型是:測定了流體進、出管排處的平均溫度,流體的流量,給出管排的幾何條件。試分析在這種條件下如何應用表6—7至表6—9的結果來確定管束的平均表面傳熱系數。
專業資料
例題 6—6 室溫為10℃的大房間中有一個
直徑為15cm的煙筒,其豎直部分高1.5m,水平部分長15m。求煙筒的平均壁溫為110℃時每小時的對流散熱量。
題解
假設:整個煙筒由水平段與豎直段構成,不考慮相交部分的互相影響,分別按水平段與豎直段單獨計算。
專業資料 計算:平均溫度
=1/2(2+t)=1/(10℃+110℃)=60℃
由附錄查得,60℃時空氣的物性p=1.060kg/㎡3,cp=1.005kJ/(kg·K),
λ=0.029W/(m·K),v=18.97x10°㎡/s. (1)煙筒豎直部分的散熱
Gr= gα,Δtl3
9.8m/s2x(1.5m)x(110-10)℃ v2
(18.97x10-6㎡/s)x(273+60)K
=2.76x1010
·由表6—10知為湍流,其
Nu=0.11(GrPr)3=0.11x(2.76x100x0.696)3=295 λ
·所以
0.029W/(m·K)
5.70W/(㎡.K) h=Nu
=295x - 1
1.5m
Φ1=πdlh(tw-t)=3.14x0.15mx1.5mx5.70W/(㎡.K)x100C=403W
專業資料
(2)煙筒水平部分的散熱
Gr= gα,Δtl3
9.8m/s2x(0.15m)3x100℃
=2.76x107 (18.97x10-6㎡/s)x(273+60)K
由表6—10知為層流。于是
GrPr=2.76x107x0.696=1.92x10
1/4 Nu=0.48x
(2.76x10)
=31.8 0.029W/(m·K)
6.15W/(㎡.K) h=31.8x
0.15m
Φ2=3.14x0.15mx15mx6.15W/(㎡·K)x100°=4345W 煙筒的總散熱量
Φc=Φ1+Φ2=(403+4345)W=4748V
專業資料
討論:煙筒的總散熱量還應包括輻射換熱。取煙筒的發射率為0.85,周圍環境溫度為10℃,則煙筒的輻射換熱量可近似地按式(1—9)估算:
Φ,=Aεσ(I-T4)
=(0.707+7.065)㎡x0.85x5.67W/(㎡·K+)x(3.834-2.83+)K4 =5660W
這里又一次看到,對這類表面溫度不很高的物體,輻射換熱量與自然對流換熱量在數量級上是相當的。
專業資料
例題 6—7 一塊寬0.1m、高0.18m的薄平
板豎直地置于溫度為20℃的大房間中。平板通電加熱,功率為100W。平板表面噴涂了反射率很高的涂層,試確定在此條件下平板的最高壁面溫度。
題解
假設:因為表面反射率高,可以近似地認為熱量全部通過自然對流散失,且熱流密度均勻分布。
專業資料
分析:此題因為平板溫度未知,而定性溫度無法在計算前確定,需要采用迭代方式。即先假定一個定性溫度,再通過計算加以檢驗和修正。
計算:先假定定性溫度tm=200C,測得空氣物性參數為
λ=0.0393W/(m·K),v=34.85x106㎡/s,P,=0.680
根據假設,得熱流密度 q=100W/(0.1mx0.18mx2)=2778V/㎡。以板高為特征長度得
9.8㎡/sx
1
x(0.18m)+x2778V/㎡ (273+200)K
Gr
=1.226x10° 0.0393W/(m·K)x(34.85㎡/s)x10-12
相應的Nu數為
0.2 Nu,=0.60(GrP,)
=0.60x(1.226x10°x0.68)2=36.74 =
h Nu.λ
36.74x0.0393W/(m·K)
=8.02W/(㎡.K) x
0.18m 專業資料
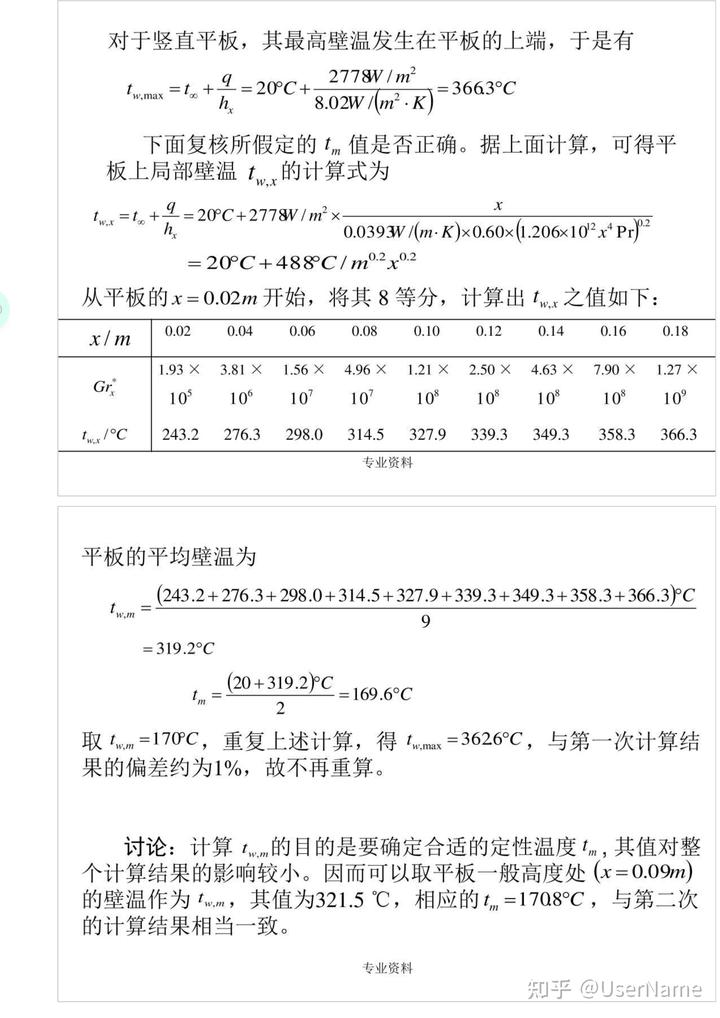
對于豎直平板,其最高壁溫發生在平板的上端,于是有
2778V/㎡ b
tw,max=t+
h
=20℃+
8.02W/(㎡·K)
=366.3℃
下面復核所假定的tm值是否正確。據上面計算,可得平板上局部壁溫t
的計算式為 x'M
tws=t+/2=20°C+2778V/㎡x h
0.0393/(m·K)x0.60x(1.206x102xPr)2 =20℃+488°C/m
0.2 0.2
x
從平板的x=0.02m開始,將其8等分,計算出t之值如下:x/m
0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16
0.18 1.93x
3.81x 1.56x 4.96x 1.21x 2.50x 4.63x 7.90x
1.27x Gr
105 106 10 10 108 10 10 108
10° ■/℃
243.2 276.3 298.0 314.5 327.9 339.3 349.3 358.3
366.3 專業資料
平板的平均壁溫為
(243.2+276.3+298.0+314.5+327.9+339.3+349.3+358.3+366.3)℃
9
=319.2℃
(20+319.2)℃
=169.6℃ 2
取twm=170C,重復上述計算,得twmax=3626℃,與第一次計算結果的偏差約為1%,故不再重算。
討論:計算twm的目的是要確定合適的定性溫度tm,其值對整個計算結果的影響較小。因而可以取平板一般高度處(x=0.09m)的壁溫作為twm,其值為321.5℃,相應的tm=1708℃,與第二次的計算結果相當一致。
專業資料
例題 6—8 一個豎封閉空腔夾層,兩壁是
邊長為0.5m的方形壁,兩壁間距為15mm,溫度分別為100℃和40℃。試計算通過此空氣夾層的自然對流傳熱量。
·題解
·分析:先計算Gr。之值,據此可以確定選用哪一個關聯式。
專業資料
計算:定性溫度為兩壁的平均溫度t
wl t
100℃+40℃ +
w2
=70℃ 2
2
從附錄查得空氣物性為:p=1.029kg/m3,v=20.02x106㎡/s,λ=0.0296W/(m·k),Pr=0.694.對于空氣
1 1 α
=2.915x10-3K-1 T
343K m
專業資料
計算Grs:
9.8m/s2x2.915x10-3K-1x60℃x(15x10-3m)
=1.444x104 Grs=
(20.02x10-6㎡/s)
而H/δ=0.5m/0.015m=33.3,可按式(6—46)計算Nu,即
-1/9
0.5 Nu=0.197x(1.444x10*x0.694)4x
=1.335
0.015 所以
0.0296W/(m·K)
2.63W/(㎡·K) h=1.335x
0.015
自然對流傳熱量按牛頓冷卻公式計算:
Φ=hAΔt=2.63W/(㎡.K)x0.25㎡x60℃=39.5W
專業資料
討論:由于夾層厚度遠小于平板的邊長,可以把封閉腔夾層近似按兩互相平行的無限大平板處理。于是,冷、熱平板間的輻射傳熱量可按式(1—9)估計為
0.5mx.6W㎡(3-3.1K =138.3εW
取冷、熱表面發射率為0.8,則Φ,=1107W。當要用實驗方法來獲得夾層中自然對流傳熱規律時,這樣大的輻射傳熱量是不合適的。為了減少由于估算輻射傳熱的誤差而對測定結果的影響,應減少表面的發射率。如果表面鍍鉻,設ε=0.05,則Φ,=6.92W,后者將使計算值的準確度顯著提高。
專業資料
例題6-9
[48,49] 熱線風速儀測速原理
。 熱線風速儀探頭的大致結構示
鎢絲
D=20μm 于圖6—26中。被測定速度的氣流流
1
L=2mm
1.-40℃ 經鎢絲的流動屬于橫掠單管的形式
。測定時對鎢絲通電,設法使鎢絲
空氣 的平均溫度保持不變,電流所產生
-支架 !_-20℃
的熱量通過對流傳熱等散失。流速越大,保持鎢絲為某個恒定溫度所需的電流強度越大,通過預先的標定,就可以從電流強度獲得被測定的流體速度。現在利用圖中所示的數據從傳熱學計算角度來確定被測定
/=150mA 的流速。鎢絲的溫度是通過測定其
電阻而得出的,其值為0.4164 Ω
圖6—26 熱線風速儀示意圖專業資料
題解
假設:電流所產生的熱量全部通過對流散失,不計輻射和熱絲端部導熱的影響。
分析:這是流體外掠單管的強制對流,可選用式(6—28)及表6—5進行計算。但是,對本例流速是被求的量,因此需要根據牛頓冷卻公式計算出表面傳熱系數,再據選定的關聯式推算相應的流速。
計算:定性溫度t=(40+20)°C/2=30℃C,相應的物性參數為
λ=0.0267W/(m·K),v=16x106㎡/s,Pr=0.701
電流的發熱量為Φ=PR=(0.150A)2x0.41642=9.37x10—3W按牛頓冷卻公式有
9.37x10-3W Φ
h=
A(tw-t)3.14x20x106mx2x103mx(40-20)℃
=3730W/(㎡.K) hd_3730W/(㎡.K)x20x106m
Nu=
=2.794 x
0.026W/(m·K)
專業資料
于是有2.794=CRe"。由于出現兩個待定常數,需要采用試湊法。先假設Re數小于4,則由表6—5得C=0.989,n=0.33,由此推得Re=33.3。可見假設不正確。再設Re數處于4~40之間,則C=0.911n=0.385,得
Re 0.385
2.794
=3.452 0.911x0.7010333 Re=3.452/0.385
=25
這一數值與假定范圍吻合,由此得氣流速度為
Rev
25x16x106㎡/s
=20m/s n
d
20x10-6m
討論:在熱線風速儀測定技術中,一般采用Nu=A+BRe"這類形式的經驗關聯式。熱線的Re數范圍一般在2~40之間。有關熱線風速儀的更多知識可參見文獻【48】。
專業資料
例題6—10 地源冷量的利用。夏天一種節能型的家用空
調的方法是利用地下一定深處的溫度低于環境溫度的特點,將熱空氣送入地下深處的
田用 管道內冷卻,然后送入房間循
冷空
熱空氣 環使用,如圖6—27所示。已知
地下:
管理 ,送風管道內徑D=400mm
風量=0.558m3/s,地下管道維持在壁溫=18℃C,房間出風溫度=25℃,要求進風
圖6-27
夏天利用地源冷量的示意圖溫度=20℃C,管道的絕對粗
糙度=2.5mm
。試確定所需 管道的長度。
專業資料
題解
假設:(1)地源的熱容量很大,管壁溫度可以維持恒定;(2)對流傳熱處于充分發展的湍流階段;(3)管道的轉彎等不予考慮,均按直管計算。
計算:定性溫度為tr=(20+25)℃C/2=22.5℃,查得物性參數為λ=0.026W/(m·K),v=15.3x106㎡/s,Pr=0.701 p=1.195kg/m3,cp=1005J/kg·K
截面平均流速
u=q(/4)=0.558m/s/3.14x(0.4m/4]=4.44m/s
4.44m/sx0.4m
Re=
=1.16x105 15.3x10-6㎡/s
專業資料 相對粗糙度為
Δ_2.5
1
Moody圖上的阻力平方區要求ReD 400 160
數大于41600.5D/2Δ)085=4160x(160x0.5/2)0.85=4160x23=95685 顯然,流動已經處于該區域,于是可以采用Nikurads公式計算阻力間:
1
1 f
=0.0325 1.74+21g
2/2)
1.74+21g
160
2 由Gnielinski 公式得
(f/8)(Re,-1000)Pr
(0.0325/8)x(1.16x105-1000)x0.701 Nu=
=395 1+12.7(f/8)05(P3-1)1+12.7x(0.0325/8)0.5x(0.701/3-1) Nu,λ_395x0.026W/(m·K)
25.8W/(㎡·K) hm
D
0.40m
專業資料
由空氣側的熱平衡關系得總換熱量為
Φ=pqc(t-t)=1.195kg/x0.558m/sx1005(kx(25-20)K =3350W
本題由于壁溫為常壁溫而且與流體溫度比較接近,應該采用對數平均溫差
(25-20)K Δt
=3.99K 25-18 In 20-18 Φ=hAΔtm=πDLhΔtm Φ
3350W L=
=25.9m πDhΔtm
3.14x0.4mx25.8W/(㎡.K)x3.99K
討論:在空調工程中習慣采用冷凍噸來表示空調負荷,1冷凍噸的制冷量為3518W,所以上述空調負荷相當于1個冷凍噸,大概可供40㎡的房間空調之用。
專業資料
例題6—11 開縫翅片效率討論(課堂/課外討論用)
為了強化氣體的對流傳熱,常常在氣體側換熱表面上設置肋片或翅片,如圖2—15所示。進一步的強化方法是在連續的翅片上開縫,從氣流在翅片上邊界層形成的角度,開縫可以切斷邊界層的連續發展,增加流體中的擾動,從而強化對流傳熱。圖(6—28)示出了一種連續翅片與一種開縫翅片。開縫翅片是在連續翅片上沖出多條縫條制成的。這些縫條分別向兩側交替地突出,成為切斷邊界層與增加擾動的元件。
25.4 25.4
R3.6
R3.6
2 (a)連續直翅片
(b)開縫翅片 圖6-28
連續直翅片與開縫翅片0.105
0.105
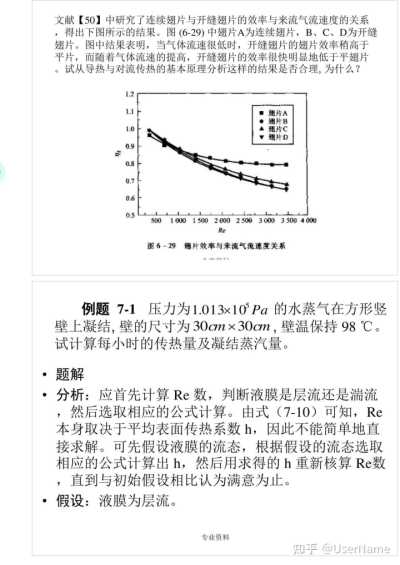
文獻【50】中研究了連續翅片與開縫翅片的效率與來流氣流速度的關系,得出下圖所示的結果。圖(6—29)中翅片A為連續翅片,B、C、D為開縫翅片。圖中結果表明,當氣體流速很低時,開縫翅片的翅片效率稍高于平片,而隨著氣體流速的提高,開縫翅片的效率很快明顯地低于平翅片。試從導熱與對流傳熱的基本原理分析這樣的結果是否合理,為什么?
1.2
1.1
■翅片A
·翅片B 1.0
翅片C
翅片D 0.9
n_{2} 0.8 0.7 0.6 0.5 500
1000 1500 2000 2500 3000 3 500 4 000 Re
圖6—29 翅片效率與來流氣流速度關系
1--人
例題 7—1 壓力為1.013x105Pa的水蒸氣在方形豎壁上凝結,壁的尺寸為30cmx30cm,壁溫保持98℃。試計算每小時的傳熱量及凝結蒸汽量。
·題解
·分析:應首先計算Re數,判斷液膜是層流還是湍流,然后選取相應的公式計算。由式(7—10)可知,Re本身取決于平均表面傳熱系數h,因此不能簡單地直接求解。可先假設液膜的流態,根據假設的流態選取相應的公式計算出h,然后用求得的h重新核算Re數,直到與初始假設相比認為滿意為止。
·假設:液膜為層流。
專業資料
計算:根據
t,=100C,從附錄查得r=2257kJ/kg。其 物性按液膜平均溫度tm=(100C+98℃C)/2=99℃C從附錄查取,得:
p=9584kg/m3,n=2.825x104Pa·s,λ=0.68W/(m·K) 選用層流液膜平均表面傳熱系數計算式(7—7)計算:
gp2x3r
h=1.13
nl(t,-tw)
1/4 9.8m/sx2257J/kgx(9584kg/m)x06sw(m. =1.13x
=1.57x10W/(㎡2.K)
專業資料 核算Re準則。按式(7—10)有
4hl(t,-tw) Re
nr
4x1.57x10*W/(㎡.K)x0.3mx2K
=59.1
2.257x10°J/kgx2.825x104Pa·s
說明原來假設液膜為層流成立。傳熱量按牛頓冷卻公式計算:Φ=hA(t,-tw)=1.57x10*W/(㎡.K)x(0.3m)x2K
=2.83x103W
凝結蒸汽量為 Φ
2.83x103W 9m
1.25x10-3kg/s=4.50kg/h r
2.257x10°J/kg
專業資料
討論:在已學習過的熱量傳遞方式中,自然對流與凝結傳熱這兩種方式的表面傳熱系數計算式顯含有傳熱溫差,自然對流層流時
h~Δt
14,而凝結液膜為層流時h~Δt—1/4。又由于凝結傳熱表面傳熱系數一般都很大,因而傳熱溫差均比較小,因此,盡可能準確地確定溫差對提高實驗或計算結果的準確度都有重要意義。本例中如t改為99℃,則傳熱強度要提高 41%。
專業資料
例題7—2圖7—14給出了壓力為1.013x10Pa的飽和水的沸騰曲線,試據圖估計實驗表面與水間的Cm之值。
·題解
·分析:由壓力為1.013x10Pa的飽和水的條件可以得出式(7—17)中的物性值,于是從圖(7—14)上每一對Δt~q的數據就可以得出一個Cw之值。由于實驗測定以及讀取數據時不可避免的偏差,相應于不同Δt~q的Cw值會有所波動,取其平均作為代表值。這里僅對一個數據進行計算。
專業資料
計算:已知s=1,飽和溫度
t=100℃。飽和水的物性從附錄查得為:
cp=4.22kJ/(kg·K),Pr=1.75,p1=9584kg/m3, y=0.0589N/m,n=0.000283Pa·s,
而p,=0.589kg/m, r=2257kJ/kg
于是
[4220J/(kg·K)}x0.00028PPa·s
9.8m/s2x958.4kg/m3 b
x 2
(2257x10J/kg)x1.753
0.589kg/m3 =3.1x104W/(㎡.K)
從圖7—14讀得:q=4x10W/㎡時,Δt=10℃。于是C=31x10w/(㎡x)x(10c)73
=0.0092 4x105W/㎡
專業資料
討論:該例題給出了如何由實驗測定結果來確定不同固—液配對時系數c之值的方法。由于是從圖中讀取數值,因此僅能作為一種估算,實際確定c值時,應該以實驗測定值為依據。幸好,計算得出的數值落在表7—1所列出的數值范圍內。
專業資料
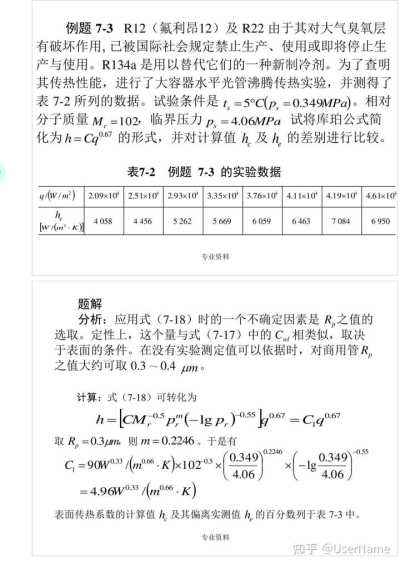
例題7—3 R12(氟利昂12)及R22由于其對大氣臭氧層有破壞作用,已被國際社會規定禁止生產、使用或即將停止生產與使用。R134a是用以替代它們的一種新制冷劑。為了查明其傳熱性能,進行了大容器水平光管沸騰傳熱實驗,并測得了表7—2所列的數據。試驗條件是t,=5℃(p,=0.349MPa)。相對分子質量M,=102,臨界壓力p3=4.06MPa 試將庫珀公式簡化為h=Cq
0.67
的形式,并對計算值h及h。
的差別進行比較。 表7-2
例題 7—3的實驗數據q/(W/㎡)
2.09x104 2.51x10 2.93x10 3.35x10+ 3.76x10 4.11x10+ 4.19x10+
4.61x10 h。
[w/(㎡·k)]
4058 4456 5 262 5 669 6059 6463 7 084
6 950 專業資料
題解
分析:應用式(7—18)時的一個不確定因素是Rp之值的選取。定性上,這個量與式(7—17)中的C相類似,取決于表面的條件。在沒有實驗測定值可以依據時,對商用管R,之值大約可取0.3~0.4 μm。
計算:式(7—18)可轉化為h=[CM,
OSpm(-1gp,)
-0.55 0.67 =C1q
0.67 萬
取R,=0.3μm,則m=0.2246。于是有C1=90W
/(㎡ 0.66 K)x102 205x 0.349 0.2246
0.349
-0.55 0.33
/
? 4.06
4.06 =4.96W0.33
/(m 0.66
K)
表面傳熱系數的計算值h及其偏離實測值h的百分數列于表7—3中。
專業資料
表7-3
例題7—3的計算值與實測值的對比q/(W/㎡)
2.09x10 2.51x10 2.93x10 3.35x10 3.76x10 4.11x10+ 4.19x104
4.61x10+ h。
[w/(㎡·k)] 3 890 4 398 4878 5337 5 766 6 120 6 170
6609 h.-hcx100%
5.9 4.8 5.3 12.9
4.9 4.1
1.3
7.3 h
討論:在無量綱的關聯式中,系數均是無量綱的,如式(7—17)中的
C,但在有量綱的經驗計算式中,如式(7—19),系數都是有量綱的,因此在將表面傳熱系數轉換成為
h=C這種形式時, 系數C也是有量綱的,在使用有量綱的實驗計算式時特別要注意這一點。請讀者進一步考慮,上式中的指數n是否為純數。
專業資料 例題7-4
在的絕對壓力下,水在的鉑質加熱面上作大容器內沸騰,試求單位加熱面積的汽化率。
題解
分析:液體的沸騰傳熱嚴格的說是一個非穩態過程:汽泡不斷地在加熱面上個別地點產生,長大,脫離,然后周圍的液體又來補充汽泡的位置,如此反復。式(7—17)(7—18)實際上給出了一個準穩態
過程的時間平均值。從本例下面的計算結果可以看出,由于汽泡的脫離,在加熱面上相當于形成了一股連續的上升氣流運動。
計算:壁面過熱度,從圖7—14知處于核態沸騰,因而可按式(7—17)求取q。
專業資料
從表7—1查的,對于水—鉑組合。從附錄查得,時水和水蒸氣的物性為:Cpl=4.22kJ/(kg·K)
Pv=0.598kg/m3 P1=958.4kg/m3
r=2257kJ/kg -3
σ=58.9x10
N/m
Pr=1.75 n=0.2825x10-3Pa·s
專業資料
代入式(7—17)得
q=0.0002825Pa·sx2257x103 J/kg
x
1/2 9.8m/s2x(958.4kg/m3-0.598kg/m3)
X 0.0589N/m
3 4220J/(kg·K)x13.9℃
=3.79x105W/㎡ 0.013x2257x103J/kg
專業資料
單位加熱面的汽化率為q_3.79x105W/㎡
0.168kg/(㎡·s) r 2257x103 J/kg
討論:這是由汽泡的上升運動而形成的一股當量蒸汽流。正是由于這股氣流所引起的對加熱面附近液體的劇烈擾動,使沸騰傳熱的強烈程度遠高于五項便的對流。如果以飽和蒸汽的密度來計算,這股質量流速相當于蒸汽以0.282m/的流速離開壁
專業資料
面向上運動。
例題7-5
試計算水在
1.01x10Pa 壓力下沸騰時的臨界熱流密度,并與圖7—14作比較。
題解
假設:加熱面足夠大,式(7—20)的應用條件滿足。
計算:稅基水蒸氣的物性數值與例7—4相同。由式(7—20)得
專業資料
=0.149x2257x103J/kgx(0.598kg/m3)1/2 b
max
1/4 [9.8m/s2x(958.4-0.598)kg/m3x0.0594N/m] =126x104W/㎡
討論:從圖7—14讀得9mm≈11.7x10W/㎡,與上述計算值的偏差為7.7%。在沸騰傳熱的計算中,這樣的數值偏差已經算是很小了。
專業資料
例題7-6
水平鉑線通電加熱,在
1.01x105Pa 的水中產生穩定膜態沸騰。已
知w—ts=654℃C,導線直徑1.27mm,求沸騰傳熱表面傳熱系數。
題解
分析:在穩定的膜態沸騰中,加熱表面的總的表面傳熱系數由沸騰及輻射兩部分組成。為確定輻射部分的大小,假定鉑絲表面的發射率為
專業資料
0.9。 計算:
Pv,由n=(w+)/2=427℃確定。從附錄查得:w=0.0505W/(m·K),n=0.0243x10-3Pa·s P1,r按t=100℃ 從附錄查得:
P1=1.75,Cpl=4220J/(kg·K),σ=588.6x10~N/m 膜態沸騰傳熱表面傳熱系數按式(7—21)計算,得
專業資料
h=0.62x
{9.8m/s2x2275x103 J/kgx0.314kg/m3x(958.4kg/m3-0.314kg/m3)x
1/4 [0.0505W/(m.K)j
x[0.0243x10-3Pa·sx0.00127mx654C] x
=281W/(㎡2·K)
據壁面發射率ε=0.9,則由式(7-23)可得
0.9x5.67xW/(㎡2·K+)x[(10.27K)4-(3.73K)4] h,
654℃C =85.3W/(㎡·K)
專業資料 由式(7-22)得 h
4/3 =(281 4/3 +85.34/3
)W4/3/(㎡·K)
4/3 由此解得h=322.9W/(㎡·K)
此值小于簡單疊加之值[366.3W/(㎡2·K)]討論:此時熱流密度為
q=322.9W/(㎡·K)x654·C=2.11x103W/㎡ 在同樣的熱流密度下,如果不發生膜態沸騰,而是處在旺盛沸騰區域內,則可據式(7—17)計算相應的表面傳熱系數。為此將該式轉換成為計算表面傳熱系數的顯示形式:
Cpl/r
0.67 h=
5人
0.33 1
σ
Pr C
IM
n.rVg(p1-pv)
將有關物性數值代入式(7—24),據表7-1取,得
專業資料 4220J/(kg·K)
h=
X 2257x103J/kg
0.67 b
0.33 1
588.6x104N/m
Pr' 0.013x
x
282.5x106kg/(m·s)x2257x103 J/kg9.m/s2x(958.4-0.958)kg/m3 =5.0W0.33/(m.66.K)q067
=5.0W0.33/(ma66.K)x(2.11x103W/㎡)067 =1.85x10+W/(㎡2·K)
可見,此時膜態沸騰的傳熱強度已經降低到旺盛核態沸騰的1/57。
專業資料
例題7-7
電熱鍋爐加熱器長度及溫壁計算。一臺電熱鍋爐每小時生產75kg140℃的飽和蒸汽。采用外徑為12mm的不銹鋼管作為安置電熱元件的外套。設計中取浸入水中的電熱元件表面熱流密度為7.75x104W/㎡。試確定需浸入水中的電熱元件的總長度以及不銹鋼管的平均表面溫度。進入鍋爐的給水溫度為20℃。
題解 假設:
(1)按表7—1所示的機械拋光的不銹鋼表面來計算;(2)電加熱功率全部用來加熱水;(3)水從20℃加熱到140℃的過程按80℃時的比熱容計算;(4)加熱管在水中加熱引起的沸騰屬于大容器沸騰,但是因工藝上的原因加熱管可能需要分層布置,這時上面的加熱面將受到位于下面的加熱面所產生汽泡的影
專業資料
響,
計算:140℃時飽和水的物性參數
為P1=926.2kg/m
Pv=1.965kg/m3 Cpl=4.287kJ/(kg·K)
n1=201.1x10-6Pa·s Pr1=1.26 σ=507.2x104N/m
r=2144.6kJ/kg 80℃C時的比熱容為4175J/(kg·K)
將75kg,溫度為20℃的水加熱成140℃的飽和蒸汽需要的熱量為
Q=75kgx[4175J/(kg·K)x(140-20)K+2144.6kJ/kg]=1.985x10J
1.985x103J 電熱鍋爐的熱流量為
5.513x10+W 3600s
按設計的熱流密度所需加熱面積為Φ
5.513x104W
2 A=-
0.711m 7.75x10+W/㎡ b
所需浸入水中的長度為
2 A
0.711㎡ L=
18.7m
πd 3.14x0.012m
這樣長的加熱段必須分成幾個彎頭來布置,而彎頭的多少取決于鍋爐容器的長度。應用式(7—17)來計算加熱面的平均壁溫。該式寫成溫
專業資料
差的形式為
1/3
1/2
CwrPr ob
1 =1
[8(p,-p,)]27,r
Cpl
1/3 1/2
7.75x10+W/㎡2x(507.2x10+N/m)
X 1/2
9.8m/s2x(926.2-1.965)kg/㎡]
x201.1x106Pa·sx2144.6kJ/kg 0.013x2144.6kJ/kgx1.26
=6.17℃
4287J/(kg·K)
不銹鋼管表面的平均溫度為tw=ts+Δt=(140+6.18)℃=146.2℃
討論:加熱管長需18m,受到鍋爐長度的限制以及工藝上的需要,
18m長度要分層布置。
這時上面的加熱面將受到位于下面的加熱面所產生的汽泡的影響。這里略去這種影響不計。由于6℃左右的加熱溫差使沸騰傳熱剛處于核態沸騰的開始階段,汽泡不會很密集,這樣的簡化處理是可以接受的。
專業資料
例題7-8
豎直水平管排上平均凝結傳熱系數的保守估計。
如圖7—28所示,在努塞爾理論分析8條假設的基礎上,進一步假定上面管子的凝結液體平靜地留到下面的管子上,不引起飛濺等現象。試導出在同一豎直排上第N根管子的平均凝結傳熱系數的計算式。
專業資料
1
1 g 1
x (a)
(c) (q)
圖7-28
推導管排平均凝結傳熱系數的模型
題解
分析:在所假設的條件下,管排上液膜的形成與流下,可以看成是一張連續的液膜在被隔成N塊離散的冷卻面上流動。根據式(7-2)
λ1 grx3p1 2
71/4 1、
8
4n,(ts-tw)x
可知:h=Cx—1,對一定的傳熱溫差與凝結條件,式中系數C為常數。
專業資料
圖7—28c中每一根管子相當于高度為Δx一段傳熱面,因此有
Δx 4C -1/4 h=
Δx-1/4 =c/
x dx 0 3 C NAx 4C
-1/4 m-N
(NΔx)-1/4 =xp
x NAx J0
3 故有
1 N-M h
N1/4
討論:得出上式的基本假定是:
(1) 液膜不飛濺;(2)液膜中的流動為層流。這種情況只有在凝結熱負荷比較小時才能近似的成立.
例題8-1
試分別計算溫度為2000K和
5800K的黑體的最大單色輻射力所對應的波長λm。
題解
分析:此題可直接應用Wien定律表示式(8—7)計算。
計算:
2.9x10-3m·K T=2000K
時, λm= 2000K
1.45x106m=1.45μm 2.9x10-3m·K
T=5800K 時, λm=專業資料
0.50x106m=0.50μm 5800K
討論:上例的計算表明,在工業上的一般高溫范圍內(2000K)黑體輻射的最大光譜輻射力的波長位于紅外線區段,而溫度等于太陽表面溫度(約5800K)的黑體輻射的最大光譜輻射力的波長則位于可見光區段。
專業資料
例題8-2
一黑體表面置于室溫為27℃C的廠房中。試求在熱平衡條件下黑體表面的輻射力。如果黑體加熱到327℃C,它的輻射力又是多少?題解
分析:所謂熱平衡就是指黑體表面溫度與環境溫度相同,即等于27℃。
專業資料
計算:按式(8—5),輻射力為
27+273
生/MGGtーと E=C.=.67W/(㎡k1)x
100 327C黑體的輻射力為
+? c.(5/10) =5.67W/(㎡.k)x(
x+=7350W/㎡ //
Eb2
討論:因為輻射力與熱力學溫度的四次方成正比,所以隨著溫度的升高輻射力急劇增大。雖然溫度僅為的兩倍,而輻射力之比卻高達16倍。
專業資料
傳熱學
例題
2010/11/11
專業資料
例題1-1
一塊厚度δ=50mm的平板,兩側表面分別維持在tw=300℃,tw2=100℃.試求下列條件下通過單位截面積的導熱量:(1)材料為銅,λ=375W/(mk)
(2)材料為鋼,λ=2.32W/(mk)
圖1—1 通過平板的(3)材料為鉻磚,
維導熱 λ=36.4W/(mk)
(4)材料為硅藻土,λ=0.242W/(mk)
專業資料 解:
銅:
-t
300-100 q=x
w1 w2 -=375x
1.50x106W/㎡ 8
0.05 鋼:
300-100 1
1- q=λ w1 w2 =36.4x
=1.46x105W/㎡ 8
0.05 鉻磚:
q=λ w1 -t
300-100
=9.28x103W/㎡ T
w2=2.32x 8
0.05 硅藻土磚:
-t
300-100 ?
w2 =0.242x
=9.68x102W/㎡ x=b
8
0.05 專業資料
例題1-2
一根水平放置的蒸汽管道,其保溫層外徑d=583mm,外表面實測平均溫度tw=48℃。空氣溫度t,=23℃,此時空氣與管道外表面間的自然對流傳熱的表面傳熱系數h=3.42 w/(㎡k),保溫層外表面的發射率ε=0.9。試求(1)此管道的散熱必須考慮哪些熱量傳遞方式;(2)計算每米長度管道的總散熱量。
專業資料
解:此管道的散熱有輻射傳熱和自然對流傳熱兩種方式。
把管道每米長度上的散熱量記為q1。
單位長度上的自然對流散熱量為q1.c=πd·hΔt=πdh(tw-t) =3.14x0.583x3.42x(48-23) =156.5w/m
每米長度管子上的輻射換熱量為
()3x=b
=274.7w/m 專業資料
于是每米長管道的總散熱量為
q1=q1,c+91,r
=156.5W/m+274.7W/m =431.2W/m
專業資料
例題1-3
一塊發射率ε=0.8的鋼板,溫度為27℃,試計算單位時間內鋼板單位面積上所發出的輻射能。
解:鋼板單位面積上所發出的輻射能為
q=8σT4=0.8x5.67x10-8W/(㎡·K4)x(27+273)4K4 =367.4W/㎡
專業資料
例題1-4
對一臺氟利昂冷凝器的傳熱過程作初步測算得到以下數據:管內水的對流傳熱表面傳熱系數h=8700W/(㎡·K),管外氟利昂蒸氣凝結換熱 表面傳數 h2=1800W/(㎡·K),換熱管子壁厚δ=1.5mm。管子材料是導熱系數 λ=383W/(m·k)的銅。試計算三個環節的熱阻及冷凝器的總傳熱系數。欲增強傳熱應從哪個環節入手?
專業資料
解:三個環節單位面積熱阻的計算分別如下:水測換熱面積熱阻:
1 1
=1.15x104㎡.K/W h 8700W/(㎡·K)
管壁導熱面積熱阻:
1.5x10-3m
=3.92x10-6㎡K/W 8
λ
383W/(m·K) 氟利昂蒸汽凝結面積熱阻:1
1
=5.56x10㎡.K/W h2
1800W/(㎡2·K) 專業資料
于是冷凝器的總傳熱系數為:
1 k
1480㎡·K/W 1δ
1 +一+
h xh
氟利昂蒸汽側的熱阻在總熱阻中占主要地位,它具有改變總熱阻的最大能力。因此,要增強冷凝器的傳熱,應先從冷凝器側入手,并設法降低這一環節的熱阻值。
專業資料
例題1-5
計算夏天與冬天站立在同為25℃的房間內的人體與環境間的換熱量。站立的人體與空氣間的自然對流換熱表面傳熱系數取為2.6,人體衣著與皮膚的表面溫度取為30℃,表面發射率為0.95。夏天室內墻面溫度取為26℃,冬天取為10℃。
專業資料
解:換熱面積
A=(3.13x0.25x1.75+3.14x0.252/4)mm=1.42㎡ 人體冬天的總換熱量:
Φ winter
=hA(tm1-ty)+εAσ(TM-)
=18.5W+154W=172.5W 人體夏天的總換熱量:
=hA(tm-t)+εA(T ① summer
=18.5W+33.4W=51.9W
同一室溫下,冬天人體的散熱是夏天的3倍多,怪不得冬天會覺得冷,而夏天則由于不能及時散熱而感到熱。
專業資料
例題2-1
一鍋爐爐墻采用密度為300kg/m的水泥珍珠巖制作,壁厚 δ=120mm 已知內壁溫度
11=600外壁溫 度t2=50℃,試求每平方米爐墻每小時的熱損失。解:為求平均導熱系數 ,先算出材料的平均溫度
λ
500℃+50℃ t
=275℃ 2
于是
λ=(0.0651+0.000105x275)W/(m·K) =(0.0651+0.0289)W/(m·K) =0.0940W/(m·K)
專業資料
代入得每平方米爐墻的熱損失為λ
0.0940W/(m·K) (1-1)
x(500℃-50℃) =b
0.120m =353W/㎡
專業資料
例題2-2
一臺鍋爐的爐墻由三層材料疊合組成。最里面是耐火粘土磚,厚115mm;中間是B級硅藻土磚,厚125mm;最外層為石棉板,厚70mm。已知爐墻內、外表面溫度分別為495℃和60℃,試求每平方米爐墻每小時的熱損失及耐火磚與硅藻土磚分界面上的溫度。
專業資料
解:δ1=115mm δ2=125mm δ3=70mm 經過幾次迭代,得出三層材料的導熱系數為3=1.12W/(m·K),1=0.116W/(m·K),3=0.116W/(m·K) 代入得每平方米爐墻每小時的熱損失為
11-14
435
W/㎡=244W/㎡ b
82 δ3
1.78 's
十 十 3
λ2 ■3
將此q值代入,求出耐火粘土磚與B級硅藻土磚分界面的溫度為
0.115m t2=1-q
A/2=495°C-244W/㎡
x
=470℃ 1.12W/(m·K) 專業資料
例題2-3
已知鋼板、水垢及灰垢的導熱系數46.4W/(m·K)1.16W/(m·K)及0.116W/(m·K),試比較厚1mm鋼板、 水垢及灰垢的面積熱阻。
解:平板的面積導熱熱阻R4=8/λ
故有 鋼板
RA
1x10-3m
2.16x10-5㎡·K/W 46.4W/(m·K)
水垢
1x10-3m R
=8.62x104㎡.K/W 人
1.16W/(m·K) 灰垢
RA
1x10-3m
=8.62x10-3㎡.K/W 0.116W/(m·K)
專業資料
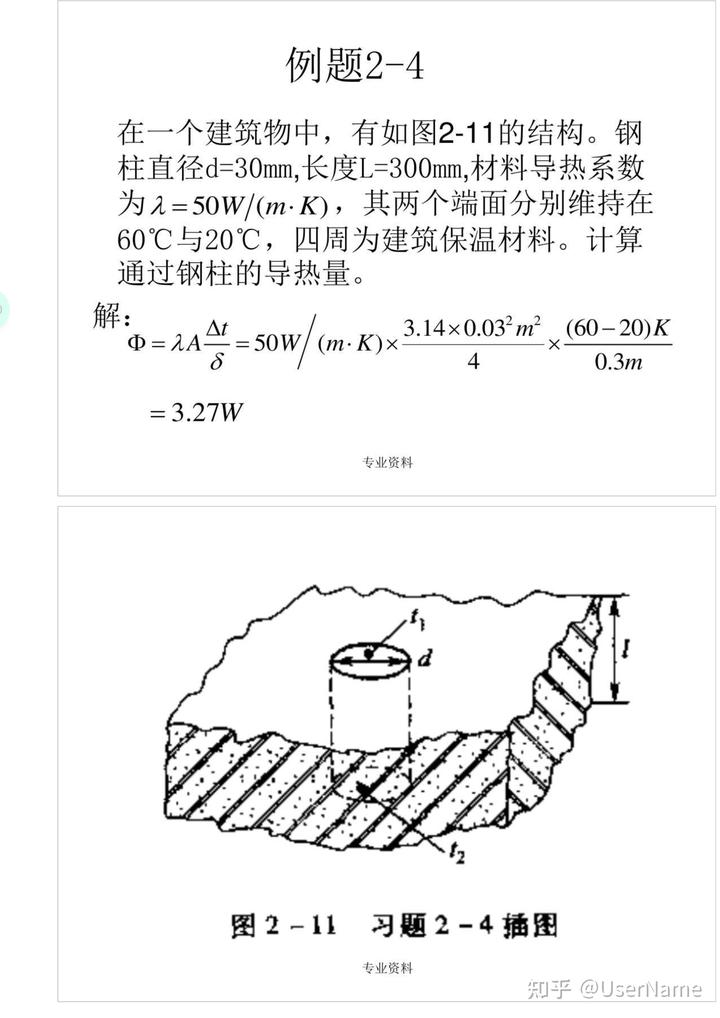
例題2-4
在一個建筑物中,有如圖2—11的結構。鋼柱直徑d=30mm,長度L=300mm,材料導熱系數為λ=50W/(m·K),其兩個端面分別維持在60℃與20℃,四周為建筑保溫材料。計算通過鋼柱的導熱量。
解:
3.14x0.032㎡ (60-20)K Φ=λA
π/5=50W/(m·K)
x 4
0.3m =3.27W
專業資料
圖2-11
習題2-4插圖 專業資料
例題2-5
為了減少熱損失和保證安全工作條件,在外徑為133mm的蒸汽管道外覆蓋保溫層。蒸汽管道外表面溫度為400℃。按電廠安全操作規定,保溫材料外側溫度不得超過50℃。如果采用水泥珍珠巖制品作保溫材料,并把每米長管道熱損失
Φ/l控制在465W/m之下,問保溫層厚度應為多少毫米?
專業資料
解:為求平均導熱系數λ,先算出材料的平均溫度
400℃+50℃
=225℃ 2
從附錄7查得導熱系數為
=0.0651+0.000105
=0.065+0.000105x225 {
?。 W/(m·K)
λ=0.0887W/(m·K)
因為d1=133mm是已知的,要約定保溫層厚度δ,須先求得
d2,將式(2——31)改寫成
2πλ ('p/p)u
(1-t2) / Ф 專業資料
即
2πλ In{d2}
(t1-t2)+In{d,}m Φ
/ 于是
In{d2}
2πx0.087
x(400-50)+ln0.133 465
=0.419-2.02=-1.601
d2=0.202m 保溫層厚度為
8=d2-d1
0.202m-0.133m
=34mm 2
2 專業資料
例題2-6
壓氣機設備的儲氣筒里的空氣溫度用一支插入裝油的鐵套管中的玻璃水銀溫度計來測量,如圖2—17所示。已知溫度計的讀數為100℃,儲氣筒與溫度計套管連接處的溫度為t0=50℃,套管高H=140mm、壁厚δ=1mm、管材導熱系數λ=58.2W/(m·K),套管外表面的表面傳熱系數h=29.1W/(㎡·K)。試分析:(1)溫度計的讀數能否準確的代表被測地點處的空氣溫度?(2)如果不能,分析其誤差有多大?
專業資料
15
H
圖2-17
溫度計套管
專業資料 據式(2——40)有
to-tf tH-tf
ch(mH) 歸并整理得
tHch(mH)-t0 tf
ch(mH)-1
本例中,換熱周長P=πd,套管截面積A=πdδ。于是,mH的值可按定義求出,即
mH= hP H= h H=
29.1W/(㎡·K)
x0.14m=3.13 VλA
Vλδ
V58.2W/(m·K)x0.001m 由數學手冊查出ch3.13=11.5。代入
計算得 1
100℃x11.5-50℃C
104.7℃C 11.5-1
專業資料
例題2-7
為了強化換熱,在外徑為25mm的管子上裝有鋁制矩形剖片的環肋,肋高H=15mm,
厚δ=1.0mm。肋基溫度為170℃,周圍流體溫度為25℃.設鋁的導熱系數λ=200W/(m·K),肋面的表面傳熱系數h=130,試計算每片肋的散熱量。
專業資料
解:采用圖2—20的效率曲線計算:
8
H'=H+-
=15mm+0.5mm=15.5mm 2
25mm =12.5mm 11
2
r2=r+H=12.5mm+15.5mm=28.0mm r2
28.0mm
=2.24 ri
12.5mm
A1=δ(-r)=0.001mx(0.028m-0.0125m)=1.55x10-5㎡ 1/2
130W/(㎡.K)
1/2 3/2
二 H22/1)
(0.0155m)
x20aw)(m.k)x1.55x105㎡ =0.396
專業資料
從圖2—20查得ηf=0.82。
如果整個肋面處于肋基溫度,一個肋片兩面的散熱量為①0=2π(㎡2-2)(to-t)
=2πx
[(0.028m)2-(0.0125m)]x130W/(㎡2·K)x(170C-25℃) =74.3W
每一個肋片的實際散熱量Φ為Φ。與肋效率η的乘積,即Φ=74.3Wx0.82=60.9W
專業資料
例題2-8
圖2—24示出了平板式太陽能集熱器的一種簡單的吸熱板結構。吸熱板面向太陽的一面涂有一層對太陽輻射吸收比很高的材料,吸熱板的背面設置了一組平行的管子,其內通以冷卻水以吸收太陽輻射,管子之間則充滿絕熱材料。吸熱板的正面在接受太陽輻射的時同時受到環境的冷卻,設凈吸收的太陽輻射為q,表面傳熱系數為h,空氣溫度為t,管子與吸熱板結合處的溫度為,試寫出確定吸熱板中溫度分布的數學描寫并求解之。
專業資料
圖2—24 平板式太陽能集熱器吸熱板
專業資料
推導:肋片的導熱微分方程與邊界條件為d2t
Φ =0式(h) + dx λ
s dt x=0,t=t;x=
=0 -
2 dx
現在進一步導出式b)中源項Φ的表達式。仿照前面的分析可以寫出
hP(t-to)+q,P
m(1-10-/1)式(k) Φ
A。 代入式(h)得
(4/--)=/
專業資料
為使式(k)成為齊次方程,定義θ=t—t
qr
。于是得 h
d2t =㎡θ dx
S
dθ x=0,θ=θ0;x=
=0
2 dx
式(2—39)顯然就是這一問題的解,而只要將其中的H用s/2來代替即可,此處不再列出。
2m0(/)
chm(x-/2) -mx
x +e
e 0
θ=θ
=θ 0
2m(1/2)
ch(m.s/2) 1+e
專業資料
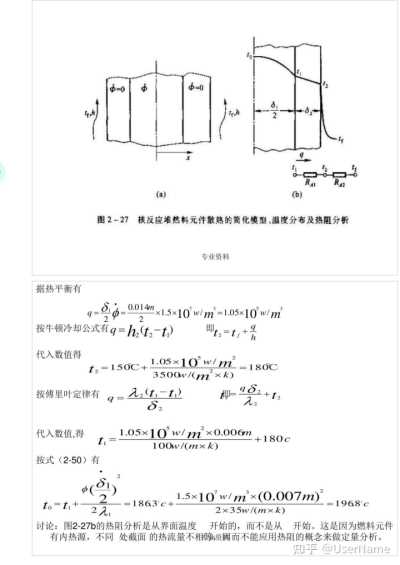
例題2—9圖2—27a給出了核反應堆中=原料元件散熱的一個放大的筒型。該模型是一個三層平板組成的大平壁,中間為δ,=14mm的染料層,兩側均為δ2=6mm的鋁板,層間接觸良好。燃料層有p=1.5x0 W/ms的內熱源
V
= =35w/(m*k)鋁板中無內熱源其
=100w/(m*k)表面受到溫度t=150℃的高壓水冷卻表面傳熱系數h=3500w/(m2*k)不及計接觸熱阻,試確定穩定工況下染料層的最高溫度,燃料層與鋁板的界面溫度及鋁板的表
面溫度并定性畫出簡化模型中的溫度分布
分析;由于對成性,只要研究半個模型即可。燃料元件的最高溫度必發生在其中心線上(X=0處)記為界面溫度及為鋁板表面溫度計為在穩態工況下燃料元件所發生的熱量必全部散失到流過鋁板表面的冷卻水中,而且從界面到冷卻水所傳遞的熱流量均相同,顧可定性的畫出截面上的溫度分布及從界面到冷卻水的熱阻如圖2—27b所示。圖中為鋁板的導熱熱阻,為表
面對流傳熱熱阻,為從燃料元件進入鋁板的熱流密度
假設(1)一維穩態導熱(2)不計接觸熱阻(3)內熱源強度為常數計算
,據熱平衡有
專業資料
Φ
Φ=0 0-Φ
RA2 (a)
(9) 圖2-27
核反應堆然料元件散熱的簡化模型、溫度分布及熱阻分析
專業資料
據熱平衡有
0.014m 9=0/20
10w/㎡=1.05x10^w/m x1.5x
2 按牛頓冷卻公式有
q=h2(t2-t,)
即t2=t x 萬
h 代入數值得
2 t2=150C+
1.05x
10°w/m
=180C 3500w/(㎡xk)
1+gb 按傅里葉定律有
λ2(t,-t1)
即 b
x2 8
2
2 代入數值,得
1.05x
<10°w/m
x0.006m
+180c t1
100w/(mxk) 按式(2-50)有
(0/1)
10'w/㎡x(0.007m)
2 1.5x
to=t1
186.3°+
=196.8℃ +
2λ
2x35w/(mxk)
討論:圖2—27b的熱阻分析是從界面溫度 開始的,而不是從 開始。這是因為燃料元件有內熱源,不同 處截面的熱流量不相等資因而不能應用熱阻的概念來做定量分析。
例題2—10 如圖2—29所示鈾燃料充裝于鋯錫合金制成的圓管中,管子內外徑分別為=8.25mm與d=9.27mm 管子呈正方形布置,管間距為17.5mm鈾棒產生功率為。管束之間有溫度為的冷卻水流過冷卻水與管子外表面的表面傳熱系數為。管子內壁與鈾棒之間的接觸熱阻相當于增加了表面傳熱系數為的一個傳遞環節,試確定穩態過程中鈾棒的最高溫度
分析:本題只有在確定了鈾棒的外表面溫度后才能應用上面的分析解,在穩態過程中,從鈾棒散出的熱量通過接觸熱阻層,鋯錫合金管傳到冷卻水中。由鈾棒外表面散出的熱量與相應總熱阻的乘積可得出鈾棒表面溫度與冷卻水溫度之間的差值。由于鋯錫合金以及鈾棒的導熱系數與溫度與關,因此是非線性問題,需采用迭代方法計算。假設(1)穩態有內熱源的導熱;(2)4根鈾棒導熱情況一樣,計算其中1根即可;(3)一維導熱,計算對單位長度鈾棒進行
計算:每米長度鈾棒外表面的散熱量為3.14
x1=8.37x
10°w/m
x(8.25x 10
)2x1m=46700w xφ=Φ
-x !p
4 鈾棒外表面溫度為
1
In(ro/r)
1 Tu=T,+?(
2πr.h,x1m
2πλ
x1m 2πr;hx1m 1
In(0.485m/0.413m)
1 =400k+46700vx
2πx0.00413nx6000w/(mxk)
2λ
2πx0.00485nx10000v/(mxk) 人分
=400k+46700vx(0.00642+0.00149+0.00328k/w=923k
專業資料
先假定鋯錫合金管子的平均溫度為600k則入2n=17.2w/(m·k),代入上式得
T■=400k+46700vx(0.00642=0.00149)+0.00328k/w=923k
至此可以應用公式(2—52)計算鈾棒的最高溫度。因此需假設鈾棒的平均溫度,這里取為1500看,λu=2.6w/(m·k)于是有:
Tmax=T+
фr2
8.73x10w/m3x0.00413㎡ =923k+
=2355k 4λ
4x2.6w/(m*k)
現在需要檢驗所嘉定的溫度是否合適,鋯錫合金管的平均壁溫為
0.0032+0.00149/2
Truben=400k+(923k-400k)x
=588k
0.00642+0.00149+0.00328
此值與600k相當接近,可以認為假設有效,鈾棒的平均溫度為
923k+2355k
イ
=1639k un
2
此值與1500k相差較遠,有必要進行修正。按這一溫度入u=2.6w/(m·k)計算得
8.73x103w/m3x0.00413㎡ T
=923k+
專業資料
=2412k max
4x2.5w/(m*k)
討論;由于鈾棒導熱系數只給出兩位有效數字,因此沒有必要做進一步的迭代,對于有內熱源的實心圓柱.球的導熱問題,穩態時外表面上的導熱量等于內熱源功率的總和,需要分析求解的僅是溫度分布
8.25mm
圖2—29 例題2—10附圖
例題2—11一根直徑為250mm的輸送水蒸氣的管道用成型的保溫材料來包覆,構成截面外形尺寸為500mmx500mm的隔熱層。設蒸汽的平均溫度為200℃,保溫層外表面溫度為60℃,保溫材料的導熱系數為0.1w/(m·k).管道長2米,試計算該管道的散熱量。
專業資料
假設:(1)穩態常物性導熱;(2)水蒸氣與管道之間的換熱阻力以及管壁的導熱阻力遠小于保溫層的導熱阻力,因而可以認為管道外表面溫度即為水蒸氣的平均溫度。
計算;采用形狀因子法來計算,所研究的對象如表2—2中第6欄所示,據已知條件有
2x3.14x2m
=16.3m 0.05m
1n(1.08x
0.25m
ф=λs(t1-t2)=0.1w/(w*k)x16.3mx(200C-60C)=228w
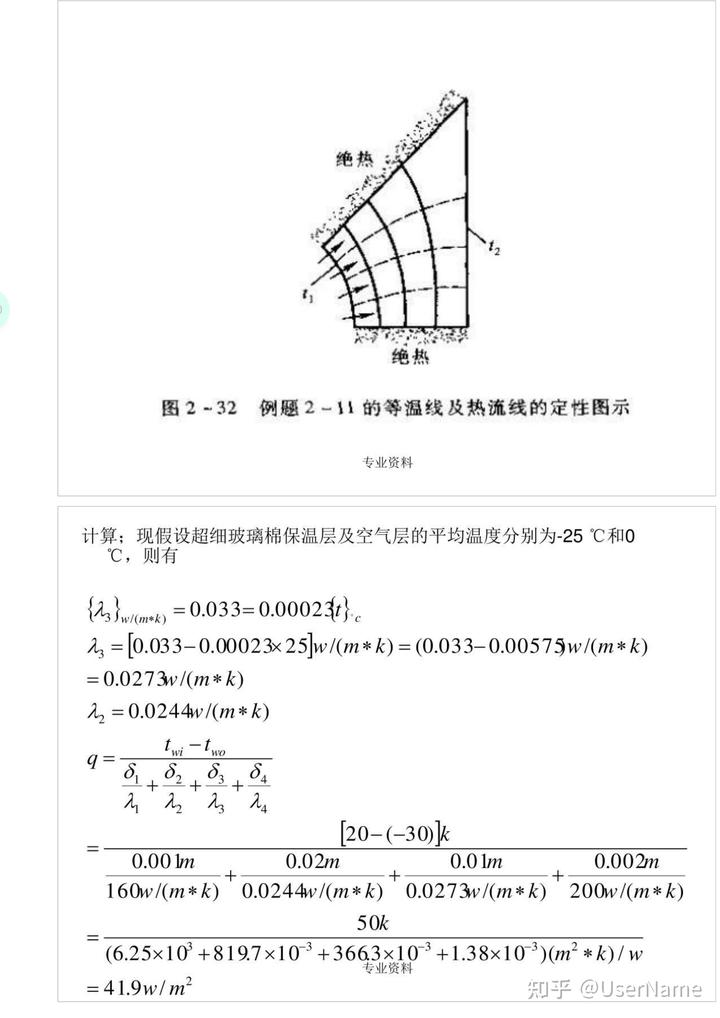
討論:形狀因子s是有量綱的物理量,其單位為米,對于所研究的問題,利用對稱性可以對八分之一區域定性畫出等溫線與熱流線如圖
專業資料
絕熱
絕熱
圖2—32 例題2—11的等溫線及熱流線的定性圖示
專業資料
計算;現假設超細玻璃棉保溫層及空氣層的平均溫度分別為—25℃和0℃,則有
{x3} w/(m*k)
=0.033=0.00023t}
x3=[0.033-0.00023x25]w/(m*k)=(0.033-0.00575)w/(m*k) =0.0273w/(m*k)
x2=0.0244w/(m*k) twi-t
O.1 b
8182+83 84 M 4
[20-(-30)]k 0.001m
0.02m
0.01m
0.002m 160w/(m*k) 0.0244w/(m*k)
0.0273w/(m*k)
200w/(m*k) 50k
(6.25x103+8197x10-3+3663x10-3+1.38x10-3)(㎡*k)/w
專業資料
=41.9w/㎡
由上面計算可見,內壁與蒙皮的熱阻不到總熱阻的1%,因而驗算平均溫度時可認為其溫度分別為20℃及—30℃,空氣層及超細玻璃棉保溫層的平均溫度為:
t3m=(20-41.9x0.8197/2)C=(20-17.2)C=2.8C
t2m=(-30+41.9x0.3663/2)C=(-30+7.7)C=-22.3C 上述兩個溫度與假定值很接近,計算有效。
在上述內外壁溫下要使熱損失減少一半,各層的平均溫度會有所變化。近似的仍以上述數據進行估算。則可得:
Q wi wO O
69 0
を
を λ3
24 b
1 w0 δ1
S2_84) δ3=λ3(
λ4 と
を
b =0.0273w/(m*k)
50
(6.25+819.7+1.38)x10
㎡
*k/w 20.75
=0.0273w/(m*k)x(2.41-0.827)㎡*k/w=0.0432m
討論(1)飛機座艙散熱量是由艙內乘客以及飛機空調系統供給的熱量來平衡的
業資料
,
在設計時為安全起見,可以認為均由空調系統所提供:(2)單從導熱系數看,空氣層的值比超細玻璃棉還小,但是要進一步減小散熱損失,不能用加厚空氣夾層的方法:這會導致夾層的自然對流,使散熱量增加
例題2—13帶肋片晶體管的冷卻。
如圖2—34a所示,有一直徑d1=4mm,高H=6mm的晶體管,其外表面套著帶縱向肋片的鋁圈,鋁圈的厚度為1mm,導熱系數為
200w/(m·k).,鋁圈與肋片系整體制造而成,肋片的高度與晶體管相同,肋片厚度均勻δ=0.7mm.鋁圈與晶體管之間存在接觸熱阻,其值為RA.ct=10—3m2xk/w.平均溫度為20℃的空氣流過晶體管,表面傳熱系數為25w/(m2·k).運行中的晶體管的外表面溫度維持為80℃,確定此時晶體管的功耗。
假設:(1)略去從晶體管頂上與底面的散熱量不計:(2)一維穩態導熱,肋片按等截面直肋看待,肋片頂端按絕熱考慮,采用增加半個肋片厚的方法來計算導熱量:(3)不計輻射換熱。
分析:從晶體管表面溫度t1到流體溫度t,導熱阻力網絡如圖所示,其中從肋片根部溫度to到流體溫度tt之間的兩個并聯的熱阻分別是從根部向四周的散熱阻力與從肋片的散熱阻力。
品體管
有縱向肋的鋁
(8)
R1 (q)
圖2—34 帶散熱肋片的晶體管及導熱網絡
專業資料
計算:四個環節的總面積熱阻如下:
RAct
103㎡*k/w
=13.3k/w =y
A
πx0.004x0.006㎡ 鋁圈導熱熱阻
Ra=
In(d2-d,)
In(3/2)
=0.054k/w 2πλH
2πx200w/(m*k)x0.006m 等截面直肋的導熱量為
φ=λA(to-t,)mth(mH)=(λAhp)2(to-t,)th(mH)
肋片的特性也可以用熱阻來表示,這個概念對于用熱阻網絡來分析問題特別有用。根據熱阻的基本定義,由上式可得通過等截面直肋的導熱阻力為
to-t
1 =
?
(xAhp)2th(mH) hx2(H+S)
25w/(㎡*k)x2x(0.006+0.0007)m 心
非
λ(Hxδ)
200w/(m*k)x0.006x0.0007㎡ =(
25w/(㎡*k)*0.0134n
1/2
=20m 200w/(m*k)x4.2x10°㎡
mH=20m-1x(0.01+0.0007)m=0.207
(λAhp)1/2=(200w/(m*k)x4.2x106㎡x25w/(㎡*k)x0.0134n)12 =0.0168v/k
專業資料 th(mH)=th(0.207)=0.204
1
故有
R
0.204x0.0168v/k
=292k/w 12個肋片的熱阻力為
R 291 f
w/k=24.3k/w Rj(12)
12
12 肋片根部面積的散熱熱阻力為
1
1
=638k/w R,=
h(πd2-12xδ)H 25w/(㎡*k)x(πx0.006-12x0.0007) 肋片根部與肋片的等效熱阻力為
R = Σ
R=(24.3-1+638')-'k/w=23.4k/w ?
于是從晶體管表面到空氣的總熱阻為R
>R=(13.3+0.054+23.4)k/w=36.8k/w ///
total
晶體管的功耗就是熱流量
(80-20)k
=1.63w 「ュー
R1ot
36.8k/w 討論:(1)肋片的效率
th(mH)
0.204
=O.986 7f
mH
0.207 肋片根部溫度為
to=t-ΦΣR=80C-1.63wx(13.3+0.054)k/w=58.2℃ 所以肋片表面的平均溫度為
tm=t,+n,(to-t,)=[20+0.986x(58.2-20)}C=(20+37.7)℃=57.7℃C 這一溫度明顯高于環境溫度,因此通過輻射還有一定的散熱量。本例中空氣為強制對流,表面傳熱系數較大,略去輻射的影響還可以接受,如何確定輻射散熱將在以后考慮
(2)如果晶體管不采用鋁制翅片,仍然假定原來的表面傳熱系數之值,則在80℃的溫度限制下,晶體管能達到的功率為
ф=hA,(to-t,)=25w/(㎡*k)x(πd,H+πd?/4)㎡x(80-20)℃ =25w/(㎡*k)x(12.56+1.26)x10-5㎡x60℃=0.21w 可見鋁制翅片的作用十分明顯。
(3)本例也可以采用肋片總效率來計算
(4)注意下列換算(a)從面積熱阻到總熱阻的換算;(b)從單個肋片熱阻到12個肋片總熱阻的換算
專業資料
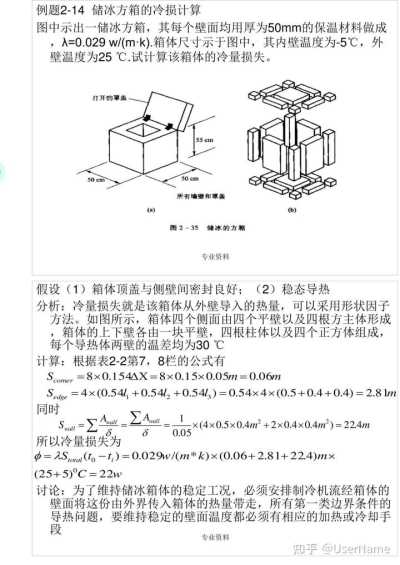
例題2—14 儲冰方箱的冷損計算
圖中示出一儲冰方箱,其每個壁面均用厚為50mm的保溫材料做成,λ=0.029w/(m·k).箱體尺寸示于圖中,其內壁溫度為—5℃,外壁溫度為25℃.試計算該箱體的冷量損失。
打開的單蓋
55cm 50cm
50cm 所有墻壁和罩蓋 (a)
(b) 圖2-35
儲冰的方箱
專業資料
假設(1)箱體頂蓋與側壁間密封良好;(2)穩態導熱
分析:冷量損失就是該箱體從外壁導入的熱量,可以采用形狀因子方法。如圖所示,箱體四個側面由四個平壁以及四根方主體形成,箱體的上下壁各由一塊平壁,四根柱體以及四個正方體組成,每個導熱體兩壁的溫差均為30℃
計算:根據表2—2第7,8欄的公式有Scomer=8x0.154ΔX=8x0.15x0.05m=0.06m
Sedge=4x(0.5411+0.54l2+0.54/3)=0.54x4x(0.5+0.4+0.4)=2.81m 同時
Σ A Σ A 1
x(4x0.5x0.4㎡+2x0.4x0.4㎡)=22.4m wall
wal S
all δ δ
0.05 //
所以冷量損失為
Φ=λStotal(to-t)=0.029w/(m*k)x(0.06+2.81+22.4)mx (25+5)℃=22w
討論:為了維持儲冰箱體的穩定工況,必須安排制冷機流經箱體的壁面將這份由外界傳入箱體的熱量帶走,所有第一類邊界條件的導熱問題,要維持穩定的壁面溫度都必須有相應的加熱或冷卻手段
專業資料
例題3-1
一直徑為5cm的鋼球,初始溫度為450℃,突然被置于溫度為30℃的空氣中。設鋼球表面與周圍環境間的表面傳熱系數為24W/(㎡.K),試計算鋼球冷卻到300℃所需的時間。已知鋼球的c=0.48kJ/(kg.K),p=7753kg/m3,λ=33W/(m.K)。
題解
假設:(1)鋼球冷卻過程中與空氣及四周冷表面發生對流與輻射換熱,隨著表面溫度的降低輻射換熱量減少。這里取一個平均值,表面傳熱系數按常數處理。(2)常物性。
計算:首先檢驗可否用集中參數法。為此計算Bi數:
專業資料
hx4/3m/(4mR}) (V/A)
Bi
Y Y
0.025m 24W/(㎡·K)x
3
=0.006 06<0.033 3 33 W/(m·K)
可以采用集中參數法。hA
24 W/(㎡2·K)x4πx(0.025m)2
=7.74x10-48* pcV 7753 kg/m3x480 J/(kg·K)x(0.025m)
據式(3-9)有
專業資料
R}3
1-1,300℃-30℃
=exp(-7.74x10r) 450℃-30℃
1-9 由此解得
t=570s=0.158h
討論 本例是在已知表面傳熱系數的條件下計算的,所設定數值的大小對計算結果影響很火。如果為了獲得金屬球與冷卻液體間的表面傳熱系數,在已知cp和幾何尺寸的情況下,你能否設計出一種方法,以通過測定金屬球非穩態導熱過程中的溫度變化而獲得所需的表面傳熱系數h之值。
專業資料
例題3—2 一溫度計的水銀泡呈圓柱形,長20mm,內徑為4mm,初始溫度為%,今將其插入到溫度較高的儲氣罐中測量氣體溫度。設水銀泡同氣體間的對流傳熱表面傳熱系數為11.63 W/(㎡·K),水銀泡一層薄玻璃的作用可以忽略不計,試計算此條件下溫度計的時間常數,并確定插入5min后溫度計讀數的過余溫度為初始過余溫度的百分之幾?水銀的物性參數如下:c=0.138kJ/(kg·K),p=13 110kg/m,λ=10.36 W/(m·K)。
題解
假設:(1)以計算水銀泡部分作為分析對象,略去玻璃柱體部分的影響;(2)常物性。計算:首先檢驗是否可用集中參數法。考慮到水銀泡柱體的上端面不直接受熱,故
πR'l
Ri
0.002mx0.02m
=0.953x10^3m A
A 2πRl+mR2 2(l+0.5R) 2x(0.020m+0.001m) Bi=
h(V/A)11.63 W/(㎡·K)x0.953x10-3m
=1.07x10^<0.05 10.36 W/(m·K)
Y
可以采用集中參數法。時間常數為
pcV 13 110kg/mx138J/(kg·K)x0.953x10-m
=1485 hA
11.63 W/(㎡·K) 專業資料
Fo=
鄭
10.36 W/(m·K)
5x60s 13110 kg/m'x138 J/(kg·K)(0.953x10-1m)2 =1.89x10
分
=exp(-Bi·o)=x(-107x10x1.89x10) =exp(-2.02)=0.133
即經5min后溫度計讀數的過余溫度是初始過余溫度的13.3%。也就是說,在這段時間內溫度計的讀數上升了這次測定中溫度躍升(從4上升到流體溫度1)的86.7%。
例題3—3 一直徑為5cm、長30cm的鋼圓柱體,初始溫度為30℃,將其放入爐溫為1200℃的加熱爐中加熱,升溫到800℃方可取出。設鋼圓柱體與煙氣間的復合換熱表面傳熱系數為140W/(㎡·K),鋼的物性參數取與例題3—1一樣的值,問需多長時間才能達到要求。題解
假設:(1)表面復合傳熱系數為常數;(2)常物性。計算:首先檢驗是否可用集中參數法。為此計算Bi:
h(V/A)_h[(ndl/4)/(ndl+2πd/4)] h dl/4 Bi=
Z/P+1 Y Y
Y
140 W/(㎡·K)x0.50mx0.3m/4
=0.049<0.05 33 W/(m·K)
0.3m+0.025m 可以采用集中參數法。因
h 4(l+d/2)
140 W/(㎡·K)x4x0.325m )
1P pc
7 753 kg/mx480 J/(kg·K)x0.05mx0.03m =0.326x10^28-
θ -1
800℃-1200℃ 0.-
30℃-1200℃
=0.342 、
據式(3-6)有
0.342=exp(-0.326x10-2t) 由此解得r=329s。
陽一
例題3—4 一塊厚100mm的鋼板放入溫度為1000℃的爐中加熱,鋼板一面受熱,另一面可近似地認為是絕熱的。鋼板初始溫度t=20℃。求鋼板受熱表面的溫度達到500℃時所需的時間,并計算此時剖面上的最大溫差。取加熱過程中的平均表面傳熱系數h=174 W/(㎡·K),鋼板的λ=34.8W/(m·K),a=0.555x10-3㎡/s。已知:Bi=0.1時,μ= 0.311 1 rad;Bi=0.5時,μ1=0.6533 rad;Bi=1.0時,μ=0.860 3 rad。
題解
假設:(1)一維問題;(2)熱物性為常數;(3)加熱過程表面傳熱系數為常數。
分析:這一問題相當于厚200mm平板對稱受熱的情形,故可以應用一維平板的分析解。計算:對于此平板
h8_174W/(㎡·K)x0.1m Bi=
=0.5 34.8W/(m·K) Y
/6=1.0
從圖3—8查得,在平板表面上8./0。=0.8。另一方面,根據已知條件,表面上的無量綱過余
溫度為
θ.1.-1500℃-1000℃
=0.51 θ0 to-t。
20℃-1000℃ 0.0m0.
θ°θ"θ 故得
θ. 0.
=0.51/0.8=0.637 θ
0000θ
據0./0。及Bi數之值,從圖3—7查得Fo=1.2,故得
r=1.2
=1.2x
(0.1m)
=2.16x10^s=0.6h ac{}{8
0.555x10-5m/s 另外,由0m=0.6370。得
=0.63700+t=0.637x(20℃-1000℃)+1000℃=376℃ 故得剖面上的最大溫差為
Δmx=500℃-376℃=124℃
例題3—5 有一直徑為400mm的鋼錠,初溫■=20℃,將它置于爐溫為900℃的爐中加熱,試計算加熱到表面溫度為750℃時所需的加熱時間。假定鋼錠可近似地視為無限長的圓柱,并取h=174W/(㎡·K)。鋼錠的λ=34.8W/(m·K),a=0.695x10-5m2/s。 題解
假設:(1)一維問題;(2)熱物性為常數;(3)加熱過程的表面傳熱系數為常數。計算:Bi=
hR 174 W/(㎡·K)x0.20m
=1.0 34.8 W/(m·K)
/8=1.0
從附錄查得,在表面上0./0=0.65。根據已知條件,表面上的無量綱過余溫度為
6..-t_750℃-900℃
=0.17 0。-1
20℃-900℃ 故得
0.0=0.17/0.65=0.262
00
據Bi=1.0及0/0g=0.262,由附錄查得Fo=0.96,故得
R2
(0.2m) t=0.96-=0.96x
=55258=1.535 h a
0.695x10-5m/s 討論:如果采用擬合公式來計算,則有
㎡=0.1700+
■=1.285 8 rad
A=1.004 2+0.587 7x[1-exp(-0.403 8x1)]=1.199 4
(M)=0.9967+0.0354x1.2858-0.3259x1.2858+0.0577x1.2858=0.6261
0.0.10
=0.17/0.65=0.262 81
所以Fo=0.898≈0.9。
這一結果與查海斯勒圖得到的數值基本一致。鋼錠的直徑實際上常常可以與其長度比較,因而更合理的計算應把它當作二維物體來處理,3.5節中將討論這一類問題。
例題3—6 一塊大平板型鋼鑄件在地坑
鑄件 中澆鑄,澆鑄前型砂溫度為20℃。設在很短時
間內澆鑄完成,并且澆鑄后鑄件的表面溫度一
80mm 直維持在其凝固溫度1450℃,試計算離鑄件底
面80mm處澆鑄后2h的溫度(圖3—13)。型砂的熱擴散率a=0.89x10—㎡/8。
題解
圖3-13
例題3-6示意圖 假設:(1)將鑄件底面以下砂型中的非穩
態導熱按第一種邊界條件的半無限大物體處理;(2)物性為常數。計算:
80x10m η
=0.5
2/at 20.89x10-6m/8x2x3 600s 由附錄查得
erf 0.5=0.5205 所以
t=1,+erf0.5(t-1,)=1450℃+0.5205x(20℃-1450℃)=705.7℃
討論:物體表面與發生相變的物質緊密接觸是形成第一類邊界條件的常見例子。本例
中,在鑄件內部基本凝固之前,假設鑄件表面仍處于相變溫度不失為一個可接受的近似處理。例題3—7 地面下的埋管是常見的工程與生活設施。考慮埋管深度的一個重要因素是
在當地的氣候條件下,埋管處的溫度不會導致管內流體凍結或凝固。以輸送工業及民用水的埋管為例,埋管處的溫度不能低于0℃。設某地冬天地表面溫度為10℃,后突然受冷空氣侵襲,地表溫度下降到—15℃,并維持45天不變,試確定此種條件下45天后地面下溫度為0℃處的位置。
題解
假設:(1)采用第一種邊界條件的半無限大非穩態導熱模型;(2)物性為常數。計算:土壤的物性取c=1840J/(kg·K),p=2050kg/m3,λ=0.52W/(m·K),于是a
專業資料
=λ/(pc)=0.138x10—6㎡/s。利用式(3—40)可寫出
(20/22)20=2/0
即
0℃-(-15℃)
(20/2)m=9'0=
10℃-(-15℃) 由附錄查得一
x≈0.6,于是 20/2
x=1.2at=1.2x(0.138x10^㎡2/sx3600sx45x24)12=0.88m
討論:土壤的熱物性參數受許多因素的影響,也與各地的地質條件有關,而本例計算結果的準確性在很大程度上取決于熱擴散率之值。例如,a值增加一倍,將使所需最小埋管深度增加41%。因此,與其他傳熱問題的計算一樣,為了獲得較準確的結果應盡量選用可靠的物性數據。還應指出,第一類邊界條件下半無限大物體非穩態導熱只是本問題的一個較粗略的模型,因為地表層的溫度并不是均勻的,地表面溫度階躍性的變化也只是一種理想化的處理。考慮這些復雜因素時分析解已無能為力,應求助于數值計算。但作為一種工程估算,本題的結果仍有其參考意義。
例題3—8 有一半無限大的物體,初始溫度t。=25℃,后其表面溫度突然上升到50℃并保持不變。試計算使表面的擾動傳遞到x=0.01m,0.1m、1.0m及10m等四個地點,且使該處發生0.1℃溫度變化所需要的時間。a=10—5㎡/s。
題解
分析:在2—2節中曾指出,傅里葉導熱定律是基于熱擾動的傳遞速度是無限大的假定,而實際物體中熱擾動的傳遞又是以有限速度進行的。這樣兩個看起來是矛盾的概念在處理一般工程導熱問題時又是如何統一的呢?本例就是為回答這樣一個問題而專門設計的。
計算:上述四個地點溫度升高0.1℃后有
1.-t(x)50℃-25.1℃
=0.996
-t。50℃-25.0℃
利用雙精度數據對誤差函數作數值積分后得η=2.0352時erfη=0.996 0006。由此得
x
=2.0352 20/2
即
4.070 42a 對四個地點的計算結果如下:
x/m
0.01
0.1
1.0
10 t/s
0.603 6
60.357
6 035.67
603 567
例題3—9 鋼錠的尺寸為28,=0.5m,26,=0.7m、28,=1m,鋼錠的λ=40.5W/(m·K),a=0.722x103m/8,求鋼錠置入爐溫為1200℃的加熱爐中4h后的最低溫度與最高溫度。其初溫1=20℃,取h=348W/(㎡·K)。
分析:該問題的解可由三塊相應的無限大平板的解得出。最低溫度發生在鋼錠的中心,即三塊無限大平板中心截面的交點上,而最高溫度則發生在鋼錠的頂角上,即三塊平板表面的公共點1:
假設:(1)物性為常數;(2)加熱過程中表面傳熱系數為常數。計算:設x.y3分別表示與三個尺度相應的坐標軸方向,則有
專業資料
gy Bi,=
348 W/(㎡·K)x0.25m
=2.15 入
40.5 W/(m·K) 0.722x10-㎡/8x4x3600s 20
Fo,=
(0.25m)2
=1.66 8
Bi,
h?2 348 W/(㎡·K)x0.35m
=3.01 40.5 W/(m·K)
Y
ar 0.722x10-㎡/sx4x3600s
=0.849 Fo,=8
(0.35m)2 Bi=-
h8,348 W/(㎡·K)x0.5m
=4.30 40.5 W/(m·K)
Y Fo,=
at_0.722x10-3㎡/sx4x3600s
=0.416 83
(0.5m)2 對平板1:
0.918 8
-1/2 μ=(0.4022+
2.15
=1.097 9 rad
A=1.0101+0.257 5(1-e-0.4271x2.15)=1.164 8 平板中心處
cos(μ1η)=cos 0°=1 平板表面處
cos(μ1η)=cosμ」=cos 62.91°=0.4555 ()
=1.1648xexp(-1.09792x1.66)=0.157 4
=1.164 8xexp(-1.097 92x1.66)x0.4555=0.071 7 (?)
對平板2:
0.918 8
-1/2 μ1=(0.4022+
3)
=1.188 1 rad
A=1.0101+0.257 5(1-e-2.4271x3.01)=1.196 1 平板中心處
cos(μ,η)=cos0°=1 平板表面處
cos(μ1η)=cos 68.08°=0.373 4 (/),
=1.196 1xexp(-1.188 12x0.849)=0.360 8
=1.196 1xexp(-1.188 12x0.849)x0.373 4=0.134 7 (?)
對平板3:
0.918 8 μ=(0.4022+
4.30
=1.274 2 rad
A=1.0101+0.257 5(1-e-.427x410)=1.226 6 平板中心處
cos(μ1η)=cos 0°=1 平板表面處
cos(μ1η)=cos 73.01°=0.292 3 (/)
=1.226 6xexp(-1.274 22x0.416)=0.6243 =1.226 6xexp(-1.2742'x0.416)x0.2923=0.182 5
(0)
據上述計算可得: 鋼錠中心溫度
=0.157 4x0.360 8x0.624 3=0.035 45 (a)(?/)(/)=θ/
1=0.035 400。+1,={0.03540x(20℃-1200℃)+1200℃]=1158.3℃ 鋼錠的頂角溫度
=0.071 6x0.134 4x0.1821=0.001 76 (■/)()(/)=8/
t=0.001 760 +1, ={0.001 76x (20℃-1 200℃)+1 200 ℃] =1197.9℃
討論:鋼錠的中心溫度及角頂溫度顯然是鋼錠中的最低與最高溫度,鋼錠的表面溫度介于其間。試利用上面計算中已獲得的數值計算此時鋼錠三個表面的中心溫度。
例題3—10 ——直徑為600mm、長1000mm的鋼錠,初溫為30℃,然后置于1300℃的加熱爐中。求置入加熱爐內4h后鋼錠中心的溫度。取表面傳熱系數的平均值h=232 W/(㎡·K),鋼錠的導熱系數λ=40.5W/(m·K),熱擴散率a=0.625x10—㎡/s。
假設:(1)物性為常數;(2)加熱過程中表面傳熱系數為常數。
計算:
0.=(0),(θ), 先討論厚28=1000mm的無限大平板:
hδ 232 W/(㎡·K)x0.5m Bi=
=2.86 λ
40.5W/(m·K) aT
0.625x10m/sx4x3 600s Fo=
=0.36 8
(0.5m) 采用擬合公式計算:
0.918 8
-1/2 ■=0.4022+
=1.175 7 rad 2.86
L161=(x A=1.0101+0.257 5(1-e
-1 17572x0.36
=0.724 5 0==1.191 Te
00
對于2R=600mm的無限長圓柱,有:
h8 232 W/(㎡·K)x0.30m Bi
=
=1.72 λ
40.5W/(m·K) at
0.625x10-3m2/sx4x3 6008 Fo=
^{
(0.30m)
=1.0 -1/2
0.0401
=1.537 8 rad ■=0.17+
1.72 A=1.004 2+0.587 7(1-e
-0,4038x1.72
)=1.2985 θm
-1.53782x1.0 =1.298 5e
=0.1220 00
專業資科
短圓柱中心的溫度為
=0.724 5x0.122 20=0.0884 16=(f/1(/1)
1n=0.08840+1,=[0.0884x(30℃-1300℃)+1 300℃]=1 187.7℃ 討論:如果把這一鋼錠作為無限長柱體處理,則將得到
1,=0.122 00,+1,=[0.1220x(30℃-1300℃)+1 300℃]=1145.1℃ 這說明短圓柱比無限長圓柱加熱得快,試分析其原因。
對于幾何形狀復雜的物體,或幾何形狀雖不復雜但邊界條件復雜的問題,分析解法已無能為力。在這種情況下,可以采用數值解法或實驗模擬法求解。由于近年來計算機應用的迅速發展,數值解法越來越顯示出其重要性,下一章將專門予以介紹。
例題3—11 有一直徑D=4cm、高H=6cm的牛肉柱體,初始溫度為10℃,后置于環境溫度為180℃的爐中加熱,表面傳熱系數為15W/(㎡·K)。問需經過多長時間牛肉的溫度才至少達到80℃?在這一過程中牛肉吸收的熱量是多少?
分析:牛肉的溫度至少達到80℃就是柱體的中心溫度應該達到這一溫度。
假設:(1)牛肉中大部分為水分,近似地用水的物性來估算;(2)牛肉柱體的各個表面同時受到加熱;(3)以(10℃+80℃)/2=45℃來確定從開始加熱到中心溫度為80℃水的物理特性,按(10℃+180℃)/2=95℃來決定計算總加熱量的物性。
計算:(1)所需時間計算由附錄并插值得
p=990.1 kg/m,c,=4.174 kJ/(kg·K),λ=64.2x10-2W/(m·K), a=15.5x10-㎡/s
本題采用Campo的擬合公式方法。(a)構成短圓柱的一—維平板計算Bi=
h8_15W/(㎡·K)x0.03m
=0.702 λ
64.2 W/(m·K)
人
0.918 8 ㎡=(0.4022+
0.702
=0.584 1
A=1.010 1+0.257 5(1-exp( -0.427 1x0.702)=1.076 8 B=
1.006 3+0.348 3x0.702
=0.903 6 1+0.547 5x0.702
8(0,7)
=1.076 8exp(-0.5841xp0) 00
=1.0768emp(-0.58418o。)x0.9036=0.9730xexp(-0.584180) 00
(b)構成短圓柱的一維圓柱
hR 15W/(㎡·K)x0.02m Bi=
=0.467 6 64.2W/(m·K)
Y
0.4349 A=0.1700+
0.4676
=0.9091
A=1.004 2+0.587 7x[1-exp(-0.403 8x0.467 6)]=1.105 3 1.0173+0.257 4x0.467 6
B
=0.888 9 1+0.598 3x0.467 6
(10)0
=1.105 3exp(-0.909|Fo。)x0.996 7=1.101 7exp(-0.909 1Fo,) °
0=1.105 3exp(-0.909 1Fo,)x0.889 9=0.983 6exp(-0.584 1Fop) °
故短圓柱的無量綱中心溫度為
=1.076 8exp(-0.584 1Fop)x1.101 7exp(-0.909 1Fo) (?) (?)=9/
at
15.5x10㎡/sx7
=1.7222x10-15x Fop=8
(0.03m)2 Fo
15.5x10(㎡/s)r
=3.8750x1045-1xt αt
R2
(0.02m)2 代入并合并同類項得:
6.
=1.186 3exp(-4.5289x104sxr)
10 θ。
17 由此解得T=1549s。
驗算:此時
Fo,=1.7222x10^4x1549=0.2667>0.2
Fo。=3.8750x10-4x1549=0.6002>0.2 (2)牛肉吸收熱量的計算
牛肉柱體的體積為
V=0.785D2H=0.785x(0.04m)2x0.06m=7.536x10^3m 將已經求出的所需時間代人,得
=0.9730xexp(-0.584 1x0.2667)=0.832 6 (?)
=0.9836xexp(-0.584 1x0.6002)=0.5693 (?)
故有
(?),=1-/0
=1-0.8326=0.1674 =1-0.5693=0.430 7 ■-1=(?)
=0.167 4+0.4307x(1-0.1674)=0.5260 [(?)-1(?)+(?)=%
Q。=pcV(t■-t)=961.9kg/mx4.21 kJ/(kg-K)x7.536x10-3㎡x(180-10)℃ =51.9kJ
Q=0.5260x51.9kJ=27.3kJ 例題3-12
·在脈管制冷機,斯特林制冷機等工程技術
中,工作介質速度的方向發生交替
變化,流體溫度發生周期性脈動,這種流動稱為交變流動(oscillating low)。假定在以空氣為介質的交變流動中,空氣在一個周期內的平均溫度為303K,脈動的頻率為5Hz,現用鋼—康銅熱電偶來測定氣流的溫度隨時間的變化。氣體流速為20m/s,熱電偶熱結點直徑d=0.9mm,熱結點的物理性質為p=8332kg/m,,=188J/(kg·K)、λ=51W/(m·K)。試問這樣的熱電偶是否能達到要求?
專業資料
題解
分析:要測定脈動頻率為5Hz(脈動周期為0.2s)的氣流溫度,則熱電偶本身的時間常數必須遠小于0.2s方可測得較準確的數值。因此,本題的計算目的是要確定所給定條件下熱電偶的時間常數。
假定:(1)熱結點是一個孤立的球體,不考慮與熱結點相連接導線的影響;(2)熱結點與空氣間的表面傳熱系數可以用流體與球體間的對流傳熱計算式來確定(這里應用第6章中的公式);(3)不計熱結點與周圍環境間的輻射傳熱。
計算:303K空氣的熱物性為v=16.0x10-6㎡/s、λ=2.67x10^2W/(m·K)、Pr= 0.701(普朗特數,反映流體熱物性的影響)。來流的Re數
u.d_20m/sx9x10m=1125 Re=
v
16.0x10㎡/s 小球的平均表面傳熱系數可按下式計算:
h=2+(0.4Re2+0.06Re232 λ1
=2+(0.4x11252+0.06x11252^3)x0.7012/5 =2+17.2=19.3
19.3x26.7x10-2W/(m·K)
=591 W/(㎡·K) 9x10m
hd_591 W/(m·K)x9x104m Bi=
=0.01 51 W/(m·K)
Y
滿足采用集中參數法的條件。所以
pcV_8332 kg/m'x188J/(kg·Kx4.5x10*m) Te=
=1.198 Ah
591 W/(㎡·K)x3
討論:此值大于溫度的脈動周期,因此該直徑的熱電偶無法測定這一交變流動的溫度隨時間的變化。需要將直徑減小到多大才能滿足要求留給讀者在習題中去完成。
專業資料
例題3—13 電熨斗燙衣料。
用電熨斗來燙平一塊厚的衣料。熨斗表面的熱流密度g0=2x10^W/㎡,衣料的初始溫度為20℃,熱擴散率a=10㎡/s,導熱系數λ=0.2W/(m·K)該衣料的燙焦溫度為180℃。如果熨斗連續在衣料表面上同一地點放置306,問衣料表面以及其下3mm處的溫度是多少?
分析:此題可以采用第二類邊界條件的半無限大物體的簡化模型來分析。
假設:(1)熨斗放在衣料上后該處仍然保持原有的形狀;(2)熨斗的熱量全部傳到衣料中;(3)常物性。
計算:計算30s后衣料表面及其下3mm處的溫度
專業資料 20
240
2x2x10W/㎡x(10-7㎡/sx30s/3.14)2 t(0,r)=t0+-
=20℃
=215.5℃ 0.2W/(m·K)
對x=3mm、t=30s,有
x
(3x10-3m)2
-=0.75 4at 4x10m/sx30s 290aπ
(20/2)00 /0-(20/)d t(x,r)=t0+
=20℃+t(0,x)=10+
=20℃+ Y
2x2x10+W/㎡x(10-1㎡/sx30/3.14)
0.2 W/(m·K)
xexp(-0.75)- 2x10*W/㎡x3x10^m
3x10m x erfc
0.2W/(m·K)
2
10m/6x30s x
=20℃+92.3℃-64.5℃=47.9℃
討論:30s后衣料的表面溫度已經超過燙焦的極限,但是3mm以下處則不到50℃,這是因為衣料的熱擴散率極低之故。
專業資科
例題3—14 蔬菜罐頭的蒸汽加熱消毒。
一直徑為10cm、高8cm的蔬菜罐頭,初始溫度為40℃,被置于飽和溫度為105℃的蒸汽中通過蒸汽凝結加熱。問80min后罐頭中的最低溫度及其所吸收的熱量。
題解
分析:蒸汽凝結對流傳熱表面傳熱系數相當大,可以認為表面熱阻為零,即Bi→■;罐頭中的最低溫度發生在罐頭的中心。
假設:(1)罐頭四周均勻受熱;(2)蔬菜的物性取為水的值;(3)罐頭內為純導熱作用,沒有對流;(4)不計罐頭金屬包殼的影響。
計算:以(40+80)℃/2=60℃計算物性有
p=983.2kg/m3,c,=4 179 J/(kg·K),λ=65.9x10-2W/(m·K),a=16x10-*m/s 對于8cm厚的平板
at
16.0x10-㎡/sx4800s Fo=
=0.48 (0.04m)
對于10cm直徑的圓柱
ar
16.0x10→5㎡/sx4800s Fo=
=0.307 R
(0.05m) 可以采用正規狀況階段的簡化解,采用擬合公式法。對平板
㎡=(a+/)
=0.4022-1=2.486 3
A=a+b[1-exp(-cBi)]=0.4022+0.918 8=1.321 0 B=
a+cBi c_0.348 3
=0.6362 1+bBi b 0.547 5
J。(η)=a+bn+c㎡2+dn=a=0.9967
()=exp(-)(0)=1.321xcxp(-2.4863x0.48)x1.0000=0.400 (/)=Aexp(-μ}Fo)B=1.321xexp(-2.4863x0.48)x0.636 2=0.255 (?), =1-(:).
=1-0.255=0.745 對于一維圓柱
=0.1700=5.8824 (/+0)=
A=a+b[1-exp(-cBi)]=1.0042+0.5877=1.591 9 a+cBi
0.257 4 =8
J+bBi b 0.5983
=0.4302 Jo(η)=a+bη+c㎡+dn'=a=0.9967
=Aexp(-㎡Fo)f(0)=1.5919xexp(-5.8824x0.307)x0.9967=0.261 (?)
(?).
=Aexp(-μFo)B=1.5919xexp(~5.882 4x0.307)x0.4302=0.113
(?),=1-(/).
=1-0.113=0.887
蔬菜罐頭
=0.400x0.261=0.104 4 (?)(?/)=4/
--105℃ ■-140℃-105℃
=0.104 4.1=98.1℃
=0.745+0.887x(1-0.745)=0.971 2 [(?)-(?)+(/)=0/0
仍然以60℃的物性值計算Q0,則有
Q=0.971 2x983.2 kg/m'x4 179 J/(kg·K)x3.14x(0.05m)2x0.08mx(105-40)K =162.9kJ
討論:分析解是對常物性問題作出的,實際物體的物理性質多少與溫度有關。但只要物性數值變化不是太大,取某個平均溫度[這樣的溫度稱為定性溫度(reference temperature)]下的物性進行計算一般足夠準確 上例中,如果計算(。的溫度取為70℃,p=977.7 kg/m',c,=4 187 J/(kg·K),則所得之值相差僅0.4%,完全在工程計算允許的誤差范圍內。
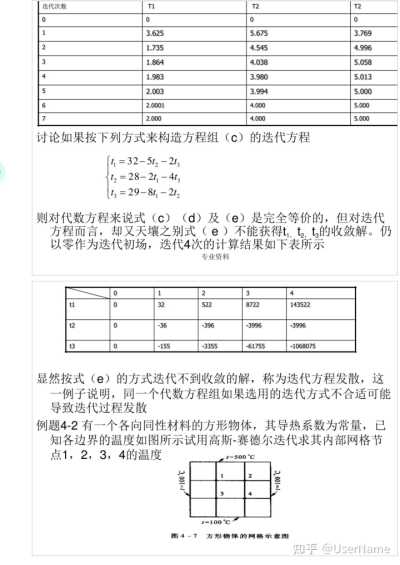
例題4—1用高斯—賽德爾迭代法求解下列方程組8t1+2t2+t3=29 11+5t2+2t3=32
21++4t3=28 解題:分析先將上式改寫為以下迭代形式
(29-2t2-t3) (32-11-2t3)
(28-21,-t2)
注意對上述改寫后的方程組,迭代收斂的條件是滿足的,假設一組初值,例如取)
=t (0) =t (0) =0
利用上述迭代方程式可以得出第一次迭代的結(0)
x
果。經過數次迭代后就可獲得所需的解。
計算:經過7次迭代后,在四位有效數字內得到了與精確解一致的結果,迭代過程的中間值如下
專業資料 ac{1}{81l5rac{1}{4}
迭代次數
T1
T2
T2 0
0
0
0 1
3.625
5.675
3.769 2
1.735
4.545
4.996 3
1.864
4.038
5.058 4
1.983
3.980
5.013 5
2.003
3.994
5.000 6
2.0001
4.000
5.000 7
2.000
4.000
5.000 討論如果按下列方式來構造方程組(c)的迭代方程
■=32-5t2-2t3 {t2=28-2t-4t3
t3=29-8t1-2t2
則對代數方程來說式(c)(d)及(e)是完全等價的,但對迭代方程而言,卻又天壤之別式(e)不能獲得t,t2.t的收斂解。仍以零作為迭代初場,迭代4次的計算結果如下表所示
專業資料 0
1 2 3
4 t1
0
32 522 8722
143522 0
t2
-36 -396 -3996
-3996 t3
-155 -3355 -61755
-1068075 0
顯然按式(e)的方式迭代不到收斂的解,稱為迭代方程發散,這一例子說明,同一個代數方程組如果選用的迭代方式不合適可能導致迭代過程發散
例題4—2有一個各向同性材料的方形物體,其導熱系數為常量,已知各邊界的溫度如圖所示試用高斯—賽德爾迭代求其內部網格節點1,2,3,4的溫度
=500℃ 1 2 3
4
r-100℃
圖4—7 方形物體的網格示意圖
200le)
t=100℃
題解
分析,這是一個三維穩態導熱問題,對于物體內部每個網格節點的溫度式(4—2)的關系適用。從形式上看式(4—2)中主對角元t的系數正好等于四個相鄰節點的系數之和,但注意到,對所計算的問題每個節點都有兩個鄰點是邊界節點,其溫度值是已知的。在寫成代數方程的通用形式時,溫度知已知的項應該歸于常數項b中,故主對角元的系數大于鄰點系數之和的要求仍然滿足,迭代法可以獲得收斂的結果。
計算;假設t(0)
=t2 (0)
=300C,t3
(0) (0) =200C 1一
4 應用式(4—2)按高斯—賽德爾迭代得
專業資料 1
(500C+100C+t+30) -x
4
1x(500+300+100+200)℃=275C 4
(1) 1
(500°C+100C+t,(1)+t(0) 十
4 1
x(500+275+100+200)℃=268.75℃ 4
1
x(100°C+100℃+1(1+0) {3}
4
1x(100+275+100+200)℃=275℃ 4
1 t(1)
(500C+100°C+t+() x
4 1
(100+268.75+100+168.75)℃=159.38℃ x
4
依次類推,可得其他各次迭代值。第1到5次迭代值于下表,其中第5次與第6次迭代的相對偏差按或4—10b已小于2x104迭代終止
迭代次數
t1/℃
t2/℃
t3/℃
t4/℃
0
300
300
200
200
1
275
268.75
168.75
159.38
2
259.38
254.69
154.69
152.35
3
252.35
251.18
151.18
150.59
4
250.59
250.3
150.03
150.15
5
250.15
250.07
150.07
150.04
6
250.04
250.02
150.02
150.01
討論:這里為了教學上的方便,只取了4個節點,進行工程計算時
,節點數的多少原則上應以下述條件為度:再進一步增加節點時
對數值計算主要結果的影響已經小到可允許的范圍內了,這時稱
數值計算的結果基本上已與網格無關,稱為網格獨立解,只有與
網格無關的數值解才能作為數值計算的結果
專業資料
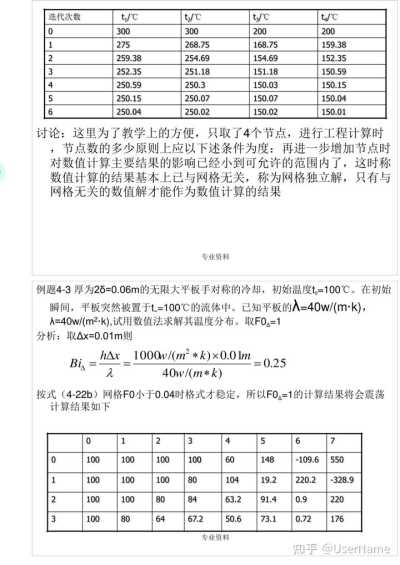
例題4—3厚為25=0.06m的無限大平板手對稱的冷卻,初始溫度t。=100℃。在初始
瞬間,平板突然被置于t=100℃的流體中。已知平板的λ=40w/(m·k),
λ=40w/(m2·k),試用數值法求解其溫度分布。取FOA=1
分析:取Δx=0.01m則
hΔx
1000v/(㎡*k)x0.01m
Bi=
40w/(m*k)
=0.25
λ
按式(4—22b)網格F0小于0.04時格式才穩定,所以FOA=1的計算結果將會震蕩
計算結果如下
0
1
2
3
4
5
6
7
0
100
100
100
100
60
148
-109.6
550
1
100
100
100
80
104
19.2
220.2
-328.9
2
100
100
80
84
63.2
91.4
0.9
220
3
100
80
64
67.2
50.6
73.1
0.72
176
專業資料
例題8-3
試分別計算溫度為1000K,1400K,3000K,6000K時可見光和紅外線輻射在黑體總輻射中所占的份額。
題解
分析:可見光和紅外線的波長范圍分別為0.38~0.76μm和0.76~1000μm。將給定溫度各自乘以0.38μm,0.76μm,1000μm,從而得到各個xT值,然后根據這些aT值,在表8—1上查得各自的能量份額Fb(0—2)
值, 再據式(8—11)計算出可見光和紅外線輻射各自占的份額。
計算:按上述方法計算得到的結果列出于下表中。
討論:可見,在T<1000K時黑體輻射中可見光所見的比例遠不到1/1000,只有溫度上升到3000K左右時可見光的比例才可達10%以上。這一關于可見光在物體自身輻射中所占的比例,總體上對大多數實際物體的輻
專業資料
射也適用。
λ1=0.38
λ2=0.76 μm
λ3
=1000 μm
μm FB(0-A2)
λT
Fb(0-k3) 溫度/K
λT
λT (1-0)9g
μm·K
μm·K
% μm·K
%
% <<0.1
760
<<0.1 1x10
100 1 000
380
1.4x10°
100 <<0.1
1064
0.07 1400
532
3x10°
100 3 000
1 140 0.14 2 280
11.7 11.3
4 560 57.3
6x106
001 2 280
% 000 9
所占
份額 可見光
紅外線 溫度/K
=F
-Fb(0-A2) F
b(λg-x2)
5(0-A3) Fb(x2-■1)
=Fu(0-k2) -F6(0-N1)
>99.9 1 000
<0.1
99.93 1 400
0.07
88.3 3000
11.6
42.6 6 000
46.0
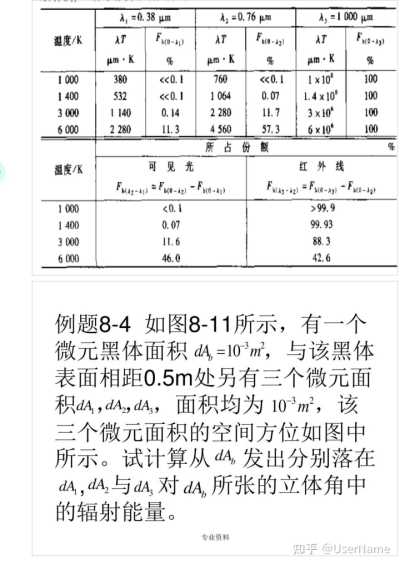
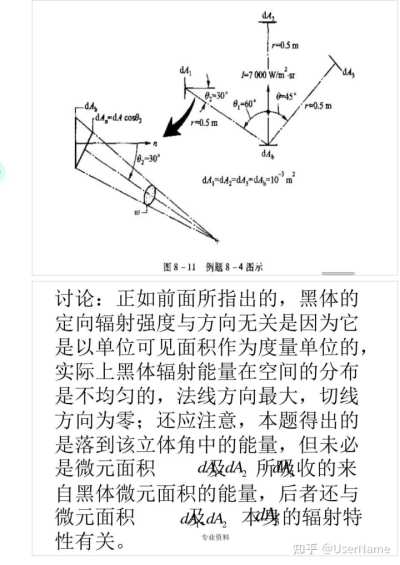
例題8—4 如圖8—11所示,有一個微元黑體面積d=103㎡,與該黑體表面相距0.5m處另有三個微元面積dA,dA2,dA3,面積均為10—3㎡,該三個微元面積的空間方位如圖中所示。試計算從dA,發出分別落在dA,,dA2與dA3對dA,所張的立體角中的輻射能量。
專業資料
題解
分析:先根據dA,dA2與dA3的大小與方向確定它們對dA,所張的立體角,然后根據式(8—15a)即可得出所求解的能量。
計算:據式(8—12)有:
dA
10-3㎡ cos 30 dΩ
=3.46x10-3sr (0.5m)2
dA
10-3㎡cos0° dΩ22
=4.00x10-3sr (0.5m)
dA
10-3㎡cos0
3 dΩ3
4.00x10
sr 專業資料
(0.5m)
dΦ(60)=1dA,cosθ,dΩ2=7000W/(㎡2.sr)x(10^-3㎡2)
-x3.46x10-3sr =1.21x10-2W
2
dΦ(0)=ldA,cosθ2dΩ22=7000W/(㎡·sr)x(10-3㎡2)x4.00x103sr =2.80x10-2W
dΦ(45)=1d4,coso,dΩ2=7000W/(㎡2.sr)x(10㎡)
rac{2}{
x4.00x10-3sr C
=1.98x10-2W
專業資料
1 } }
r=0.5m
1 dA
1=7000 W/m-sr
dA3 θ2=30°
0-45°
r=0.5m dA=dA cosθ2
r=0.5m dAp -3 2
dA,=dA2=d43=dA=10m 圖8—11 例題8—4圖示
討論:正如前面所指出的,黑體的定向輻射強度與方向無關是因為它是以單位可見面積作為度量單位的,實際上黑體輻射能量在空間的分布是不均勻的,法線方向最大,切線方向為零;還應注意,本題得出的是落到該立體角中的能量,但未必是微元面積
d及dA2所吸收的來自黑體微元面積的能量,后者還與微元面積
d及dA2本身的輻射特專業資料
性有關。
例題8—5 試計算溫度處于1400℃C的碳化硅涂料表面的輻射力。
題解
分析:碳化硅涂料是非導體,可取ε=8n。
計算:由表8—2查得,碳化硅涂料在1400℃C時的εn=0.92,亦即ε=0.92。按照式(8—18),其輻射力為
(14070+273)x E=εC
100
=409x103W/㎡=409kW/㎡
討論:一般工業手冊中給出的發射率常為法向發射率,選用時應注意表面類型與狀態而作相應修正。對于本例,要注意給定的溫度范圍是與發射率范圍相對應的。
專業資料
·例題8-6
.
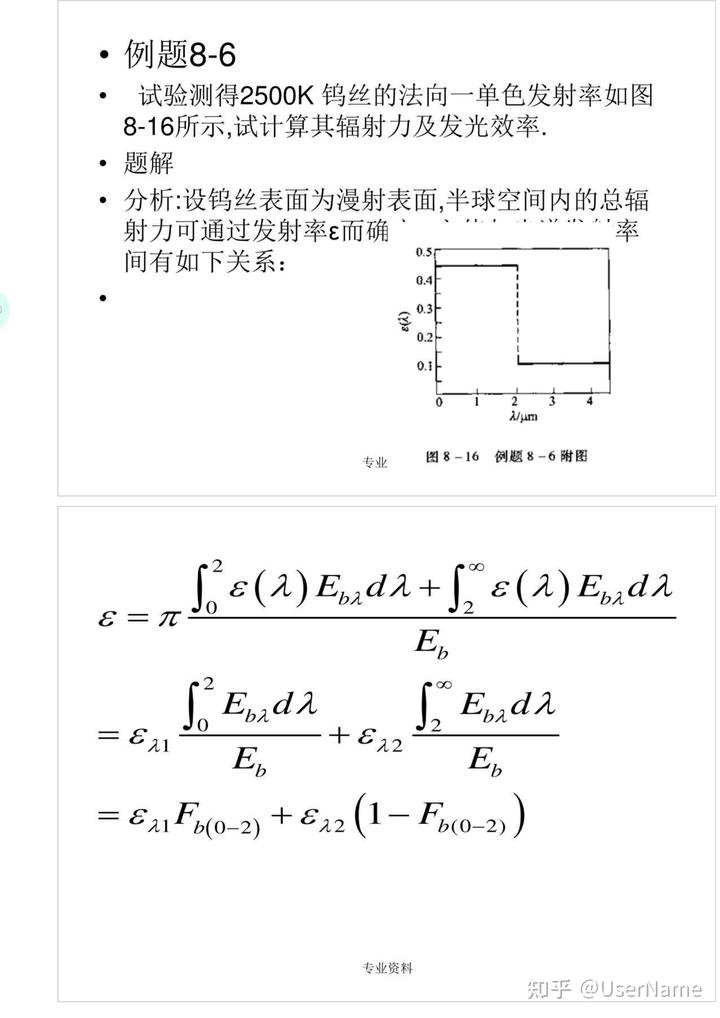
試驗測得2500K鎢絲的法向一單色發射率如圖8—16所示,試計算其輻射力及發光效率.
·題解
·分析:設鎢絲表面為漫射表面,半球空間內的總輻射力可通過發射率ε而確
率 間有如下關系:
0.4 0.3 40 0.2 0.1 0 1 2
λ/μm 專業
圖8—16 例題8—6附圖8
(x)Eb2dλ+2
ε(x)Ebadλ 1=3
Eb 2
8 Ebdλ
Ebadλ 07
2
3+ 3=
λ1
λ2 Eb
Eb F
十 b(0-2)
(1-Fb(0-2)) 3=
3 λ1
λ2
專業資料
計算:AT=2x10-6μmx2500K=5000μm·K, =0.6341
Fb(0-2)
ε=0.45x0.6341+0.1x(1-0.6341)=0.322
2500
K E=8P,=0.332x5.67W/(㎡·k1)x
100 =7.13x105W/㎡
專業資料
取可見光的波長范圍為0.38~0.76μm,則λT=950μm·K,1T=1900μm·K。由表8—1,近似地取F
=0.0003, b(0-0.38)
Fb(0-0.76)
=0.0521。于是,在可見光范圍內發出的能量ΔE為
2500
K ΔE=(0.0521-0.0003)x0.45x5.67W/(㎡.K)x(
100 =5.16x104W/㎡
ΔE_5.16x104W/㎡ 發光效率為η=
=0.0727=7.27% E
7.16x105W/㎡ 專業資料
·討論:自從愛迪生發明第一只白熾燈以來,
已經歷了百余年。白熾燈由于燈絲的工作溫度相對較低,熱輻射中可見光的比例甚少,因此發光效率不高。大部分能量都作為不可見的紅外輻射的能量而沒有予以利用。發展新的固態光源(如發光二極管,LED)作為白熾燈,熒光燈以后的第三代照明技術是節約能源的重要措施,已經引起世界各國的重視。
專業資料 例題8-7
一火床爐的爐墻內表面溫度為500K,其光譜發射率可近似地表示為:
λ≤1.5μm時ε(x)=0.1;λ=1.5~10μm時ε(λ)=0.5; x
10μm時ε(x)=0.8。爐墻內壁接受來自燃燒著的煤層的輻射,煤層溫度為2000K。設煤層的輻射可以作為黑體輻射,爐墻為漫射表面,試計算其發射率及對煤層輻射的吸收比。
題解
分析:爐墻的發射率可以按定義由以下分段積分來獲得:
專業資料
21
λ2 E
dλ
E dλ
J2
dλ 吖
29日 bλ
bλ 3=3
+8x3
Eb +8x2
Eb 12
Eb 上 b(0-21)
F b(x1-x2) + 8x3 b(x2-00)
x 3=
3+ 21
λ2
按定義,爐墻的吸收率為:a(x,T,)E2(T2)d =0
{2} E
b2(I2)dλ
由于爐墻為漫射體,所以有ε(λ,T)=α(λ,T),
由此可得: b(0-21)
A b(11-λ2)
23 F
b(x2-00) A
λ2 3=0
21
十 3
+ 3
專業資料
·計算:對于爐墻的發射率,有:AT=1.5μmx500K=750μm·K,F
=0.000
b(0-11) ■T1=10μmx500K=5000μm·K,F
=0.634
b(0-x2) 所以:
ε(TG)=0.1x0.000+0.5x0.634+0.8x(1-0.634)=0.61
爐墻吸收的是2000K時的輻射,應按2000K計算λT,即:
專業資料
AT2=1.5μmx2000K=3000μm·K,F
b(0-21)
=0.274 AT2=10μmx2000K=20000μm·K,F
=0.986
b(0-x2)
a(T,T2)=0.1x0.274+0.5x(0.986-0.274)+0.8x(1-0.986)=0.395 討論:由計算得ε(T,)=0.61,而α(T,T2)=0.395,α≠8。
這主要是由于在所研究的波長范圍內,α(λ)不時常數所致。
專業資料
·例題8-8
·人造衛星表面對太陽輻射吸收率的允許值的估計。
R=1m
ε=0.75
G3 圖8—27 例題8—8圖示
專業資料
·如圖8—27所示,一個研究衛星繞地球的近極點的軌道運行,使得衛星可以總是受到太陽的直接輻射。為了姿態控制,衛星繞與軌道相一致的軸旋轉。衛星呈球形,外徑1m,其內的各種電子器件的散熱量為1250W。衛星的外殼需要維持在265~305的溫度。已知殼體的發射率為0.75,其溫度均勻。試估算能允許的衛星表面對太陽能輻射的吸收率。
專業資料
·題解
·分析:衛星與太陽間的輻射作用是衛星最主要的傳熱過程,因此可假設不考慮衛星與地球間的輻射換熱,宇宙空間按0K的物體處理,則衛星表面得到的是太陽的輻射和內部電子器件的散熱量,傳遞到宇宙空間的是其自身輻射,根據熱平衡有:
專業資料
a,G,A+фc=εσT4A
其中α,是衛星表面的吸收率,A為衛星接收太陽輻射的面積,?是電子器件的功率。于是有
4πR2εσT4-φ α
πR2G
計算:衛星需要維持外表面溫度在265K到305K之間。因此最小與最大的吸收率分別為:
4πx1㎡x0.75x5.67x10-8W/(㎡.k4)x(265K)4-1250W αs,min
πl㎡x1367W/㎡ =0.323
4πx1㎡x0.75x5.67x10-8W/(㎡2·k+)x(305K)4-1250W αs,max
πl㎡x1367W/㎡ =0.786
專業資料
·討論:為使衛星表面對太陽輻射的吸收率達到所需的值,可對表面材料敷設專門的涂層。在太空飛行的物體,輻射是其散熱的唯一方式,所以航天事業是促進輻射傳熱研究發展的主要動力之一。本章宜用的輻射名著的作者就是長期從事美國航天事業的研究者。
專業資料
·例題8-9
·測定吸收比與發射率的實驗。
·圖8—28給出了一種測定表面發射率與吸收比的裝置示意圖。一直徑為30mm的圓柱形試樣受水冷卻,被置于一個大的腔體的右上角。殼體內壁面為漫灰體,發射率為0.8。該試樣的光譜反射率如上圖所示。試驗中測得穩定工況下試樣表面溫度為
T,=300K,腔體內表面溫度為T,=1000K,其中充滿1000K的空氣。冷卻水帶走的熱量為24.4W。試計算該條件下試樣的吸收比與發射率,以及試樣表面與空氣間的對流傳熱系數。試樣是不透明的漫射體。
專業資料
一試樣
1 0.8 0.2 0 0
246 8
01
2/μm
圖8—28 一種測定表面發射率,吸收比的裝置示意圖
專業資料
·題解
·分析:熱平衡時,試樣從大腔體得到的輻射能,從空氣對流得到的能量,減去其自身輻射應等于被冷卻水帶走的熱量。故有:
Φcool=A[αG(T)+Φcomv-εE,(T,)]= A[αG(T)+h
conv
(T,-T)-εE,(T)] 為了計算h
需要先求出發射率和吸收比。C
腔體的體積很大,它對試樣的投入輻射就是1000K下的黑體輻射。因為試樣不透明,所以光譜吸收率α(λ)=1—p(λ)。據此可按定義計算試樣的吸收率等。
專業資料
·計算:試樣的吸收率為
α=a()Gdλ/G=1-)(1000K)dλ/(1000K)
十
b(0-4)
+ α=(1-p(x))Fb(0-3)
(1-p(3))Fb(q-x2)=(1-p(3))F (1-p(1))(1-F)(0,-x1)
據表8-1,AT=4x1000μm·K=4000μm·K,Fb(0-4)
=0.4813。 故有:α=(1—0.2)x0.4813+(1—0.8)x(1—0.4813)=0.481
按發射率的定義。有 E(T)
I(x)Em2(300K)dλ/E,(300K)= E,(T)
(1-p(x))F
十
-(1-p(22))(1-FD(0-x1) b(0-■)
專業資料
據表8-1,AT,=4x300μm·K=1200μm·K,F
=0.002
b(0-21) ε=(1-0.2)x0.002+(1-0.8)x(1-0.002)=0.2
根據發射率和吸收比之值可以得出對流傳熱的表面傳熱系數之值為:
1
Pa-aG(T,)+eE,(T) hcom
T,-T,
24.4W 1
3.14/4x0.03㎡
0.481x5.67x108W/(㎡2·K4)x(1000K)++ (1000-300)K
0.2x5.67x108W/(㎡2·K4)x(300K) =10W/(㎡·K)
專業資料
討論:讀者也許要問:那么p(λ)又是怎樣測定的呢?如圖8—28所示,如果在大腔體的底面中間開一個極小的孔,可以分別測出從腔體左右兩個頂面上發出的總的輻射能。由于試樣本身溫度較低,可以認為試樣向外發射的主要是反射的能量,對波長λ,反射能量正比于p(x)G2,從圖中的A方向用測定定向輻射強度的儀器可以測定這份能量,而從B方向則可測定正比于E2(T1)的能量,因為G1(T)=Eba(I,),所以兩者之比既為p(x)。
專業資料
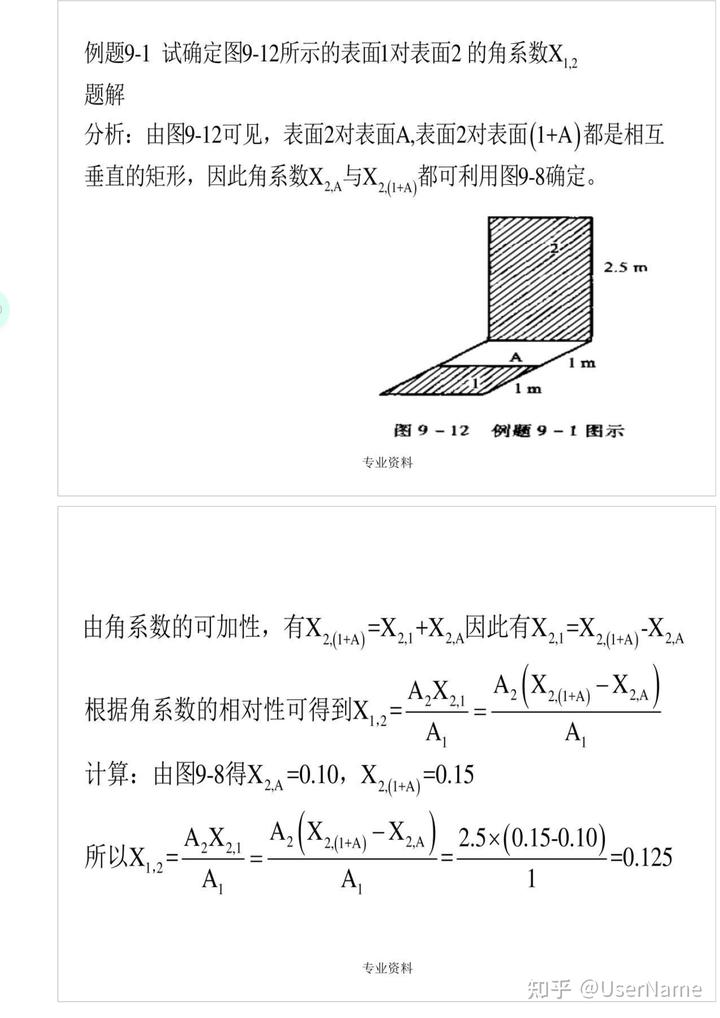
例題9—1 試確定圖9—12所示的表面1對表面2的角系數X
1,2 題解
分析:由圖9—12可見,表面2對表面A,表面2對表面
(1+A)
都是相互 垂直的矩形,因此角系數X,與X
都可利用圖9—8確定。2.A
2,(1+A)
2.5m A
1 m
1m
圖9—12 例題9—1圖示專業資料
由角系數的可加性,有X
2,(1+A) =X
因此有X
=X 2,(1+A)
-X X+
2,1 2,A
2,1
2,A +
A2X
A2(X
2,(1+A) 根據角系數的相對性可得到X
2,1
2,A 1,2
A1
A1 計算:由圖9—8得X,A=
=0.10,X
=0.15 2,A
2,(1+A)
X- A2X
A2(X 2,(1+A)
2.5x(0.15-0.10) 所以X
2,1
2,A
=0.125 1,2
A1
A1
1 專業資料
討論:利用這樣的分析方法可以得出不少幾何結構
的角系數,習題中將有更多這樣的例子。采用代數分析法時最終得到的答案往往是一個比較小的數。因而計算時要注意有效數字的位數問題。
專業資料
例題9—2液氧儲存容器為雙壁鍍銀的夾層結構(圖9—17),外壁內表面溫度tM=20℃,內壁外表面溫度tw2=—183℃,鍍銀壁的發射率ε=0.02。試計算由于輻射傳熱每單位面積容器壁的散熱量。
圖9—16 平行平板間輻射
圖9—17 液氧儲存容器示意圖傳熱的示意圖
專業資料
題解
分析:因為容器夾層的間隙很小,可認為屬于無限大平行表面間的輻射傳熱問題。容器壁單位面積的輻射散熱量可用式(9—16)計算。計算T1=tw1+273K=(20+273)K=293K
Tw2=tw2+273K=(-183+273)K=90K co(F)(T)
5.67W/(㎡2·k+)x[(2.93k)'-(0.9k)*] q1.2
=4.18W/㎡ 1
1
1
1 -1
-1 +
+
0.02 0.02 3 3
專業資料
討論:采用鍍銀壁對降低輻射散熱量作用極大。作為比較,設ε1=82=0.8,則將有q12=276W/㎡,即散熱量增加66倍。
如果不采用抽真空的夾層,而是采用在容器外敷設保溫材料的方法來絕熱,取保溫材料的導熱系數為0.05W/(mn·k)
(這已經是相當好的保溫材料了),則按一維平板導熱問題來估算,所需的保溫材料壁厚δ應滿足下式:
[20-(-183)]K 4.18W/㎡=0.05W/(m·k)x
δ δ=2.43m
因此可見抽真空的低發射率夾層保溫的有效性。
專業資料
例題9—3 一根直徑d=50mm、長度1=8m的鋼管,被置于橫斷面為0.2mx0.2m的磚槽道內。若鋼管溫度和發射率分別為t,=250℃,ε1=0.79,磚槽壁面溫度和發射率分別為t2=27℃C,ε2=0.93,試計算該鋼管的輻射熱損失。
題解
分析:這是一個三維問題,但是因為l/d>>1,可以近似地按二維問題處理,而直接應用是(9—15)計算鋼管的輻射散熱損失。
計算:
AC()(F)
3.14x0.05mx8mx5.67W/(㎡·k)x[(5.23k)*-(3.00k)+
1
3.14x0.05
1
x 1/4(1/-
0.79 4x0.2
0.93 =3.710KW
專業資料
討論:這一問題也可以近似地采用A,/A2≈0的模型。此時有φ=C,AC(π)-()
=0.79x3.14x0.05mx8mx5.67W/(㎡.k4) x[(5.23k)+-(3.00k)+]=3.754KW
與上述結果只相差1%.
例題9—4 一直徑d=0.75m的圓筒形埋地式加熱爐采用電加熱方法加熱,如圖9—18所示。在操作過程中需要將爐子頂蓋移去一段時間,設此時筒身溫度為500K,筒底為650K。環境溫度為300K。試計算頂蓋移去期間單位時間內的熱損失。設筒身及底面均可作為黑體。
專業資料
題解
分析:從加熱爐的側壁與底面通過頂開口散失到廠房中的輻射熱量幾乎全部被廠房中的物體吸收,返回到加熱爐內的比例幾乎為零,因此可以把頂蓋開口處當作一個
3
T■=300 K
500K
650K 圖9-18
例題9-4
的圖示 專業資料
假想的黑體表面,其溫度則等于環境溫度,這樣就形成了由3個等溫表面組成的黑體封閉腔。加熱爐散失到廠房中的輻射能即為ф=23+ф,3=A2X23(Eb2—Eb3)+
A,X13(Eb1-Eb3)
計算:據角系數圖9—9,r2/1=0.375/1.5=0.25,1/r,=1.5/0.375=4,得X13=0.06,X12=1-0.06=0.94
3.14x0.752/4 公
據相對性得X
X
x0.94=0.118 2,1
1,2 A
3.14x0.75x1.5 c
專業資料
1=1.5m
再據相對性得X
=X
,故最后得 2,1
2,3
Φ=3.14x0.75mx1.5mx0.118x5.67W/(㎡·K+)x[(5K)-(3K)]+ 3.14
(0.75m)2x0.06x5.67W/(㎡2·K4)x 4
(6.5K)#-(3K)+]=1286W+256W=1542W
討論:在上述計算中利用9.1節中的式(c)計算兩個黑體表面間的輻射傳熱,該兩個表面并未形成封閉系統。這里要特別指出,
專業資料
只有對于黑體表面,不形成封閉腔的兩表面之間的輻射傳熱計算才具有確定的結果;而對于灰體表面,這樣的計算不能得出確定的結果,其數值將隨環境條件的不同而改變。鑒于這一原因,
本書不討論不構成封閉腔的任意兩表面間的輻射傳熱,而把注意力集中到工程計算最感興趣的問題——一個表面通過輻射傳熱所傳遞的凈輻
射傳熱量。對于這種計算,必須采用封閉腔的模型。
專業資料
例題9—5 兩塊尺寸均勻為1mx2m、間距為1m的平行平板置于室溫t3=27℃的大廠房內。平板背面不參與換熱。已知兩板的溫度和發射率分別為
t,=827℃、t2=327℃和ε1=0.2、ε2=0.5,試計算每塊板的凈輻射散熱量及廠房墻壁所得到的輻射熱量。
題解
J,1.75㎡2
E2=aT2 10-19g
?口 -2
-2 2.0m
0.5m
-2 0.699m
0.699m
Eb3=0T3=/3 圖9-24
例題9-5的網絡圖 專業資料
分析:本題是3個灰表面間的輻射傳熱問題。
因廠房墻壁表面積A3很大,其表面熱阻1—83/(ε3A3)可取為零。J3=Eb3是個已知量,而其等效網絡
圖如圖9—24所示。
計算:根據給定的幾何特性X/D=2、Y/D=1,由圖9—7查出:X1,2=X2,1=0.285而X1.3=X2.3=1-X
X1,2
=1-0.285=0.715 計算網絡中的各熱阻值
1-81 1-0.2 =2.0m2
1-82
1-0.5 =0.5m
-2 2
ε2A2
0.5x2m
2 0.2x2m
A3 1
1
1
1 -2
/ 1.75m
=0.699㎡ A,X1,2
2㎡x0.285
A,X,
2㎡x0.715 1,3
1
1
-2 =0.699m 2
A2X2.3 2m x0.715 專業資料
以上各熱阻的數值已標出在圖9—24上。
對節點J1J2應用直流電路的基爾霍夫定律,得:J1:
E J
J2-J1
E
-J -
b3
, 1
0 2
1.75
0.699 J2:
J1-J
E -J E
一 2
,
( b3
b2 、
九 1.75
十 0.699
0.5
0
4 而
E
=5.67W/(㎡2·K4)
1100
K !
Co(/10)
x b1
100
=83.01x103W/㎡=83.01KW/㎡ E
?
(と)A39 (
K b2
0
=7.348x103W/㎡=7.348KW/㎡ 專業資料
E C 100 T3
=5.67W/(㎡·K4)
300
K_{ b3
二
X
001
=459WV/㎡=0.459KW/㎡ 將E
E E
值代入方程,聯立求解得b2
b3 J1=18.33KW/㎡
J2=6.347KW/㎡ 于是板1的輻射傳熱量
E b1-J
83.01x103W-18.33x103W b1
?1 1-81
2 V'3
=32.34x103W=32.34KW 專業資料
板2的輻射傳熱量
Eb2-J2
7.348x103W-6.437x103W Φ2=
1-82
2 ε2A2
=1.822x103W=1.R822KW 廠房墻壁的輻射傳熱量
E -J ? -J2 -J、 3
公山 b3
=Φ
c{邑) 0.699
0.699
2
0.5 =-(32.34x10W+1.822x10W)=-34.16KW 專業資料
討論:表面1、2的凈輻射傳熱量中的?及?2均為正值,說明兩個表面都向環境放出了熱量。按能量守恒定律,這份能量必為墻壁所吸收。上述結果中的負號就表示了這一物理意義。又,本題為簡化分析,設平板1、2的背面不參與輻射傳熱。如果設平板1、2的背面分別為表面4、5,其溫度及發射率分別與其正面的一樣,試畫出這時的等效網絡圖,并分析表面熱阻R4.5,R
R R R
之值。 4.1
4,2, 5,1 5,2
專業資料
例題9—6 假定例題9—5中大房間的墻壁為重輻射表面,在其他條件不變時,試計算溫度較高表面的凈輻射散熱量。
題解
分析:本例題與例題9—5的區別在于把房間墻壁看成是絕熱表面,于是
房間墻壁不能把熱量傳向外界,其輻射網絡見圖9—23c。因其他條件不變,上例中各熱阻值及E。和E2之值在本例中仍然有效。
計算:
1-8
1-82=0.5m R
=2㎡2,R2=
82A2 V'3
1
1
=0.699㎡2,R23=R13=0.699㎡2≈0.7㎡ -2
R1.2=
1.75m ,P
1,3 A,X1.2
A1X1.3
專業資料 EB1=83.01kW/㎡,Eb2=7.348kW/㎡
串、并聯電路部分的等效電阻為
1 1
1
1 R
-2
-2 百
2 R
R
1.75m
0.7m
0.7m 1,2
金 + 1,3
十 2
=1.29m
1 所以
R
=0.78㎡- ba
1.29㎡ 專業資料
在Eb和Eb2之間的總阻值為
、 R=R
R
+R2=(2+0.78+0.5)m +
3 1 ba
=3.28m-2 溫度較高的表面的凈輻射散熱量為
E -E
83.01x103W/㎡-7.348x103W/㎡ b1
b2 Φ1.2= ΣR
3.28m-2 =23.06x103W=23.06kW
專業資料
討論:表面3改為重輻射面后輻射傳熱情況發生了重要變化:首先高溫表面1的凈換熱量減少了約29%;其次表面2在上例中也是一個凈放熱的表面,而這里則稱為一個凈吸熱的表面。所以,在進行多表面系統輻射傳熱的計算時,是否確認其中某個表面為重輻射面必須謹慎。從數學、
物理建模的角度看,這相當于要正確地給出熱邊界條件。
專業資料
例題9—7 有一輻射采暖間,加熱設施布置于頂棚,房間尺寸為4mx5mx3m,見圖9—25。根據實測已知:頂棚表面溫t1=25℃,ε1=0.9;邊墻2內表面溫度t2=10℃,82=0.8;其余三面邊墻的內表面溫度及發射率相同,將它們作為整體看待,統稱為A3,t3=13℃,83=0.8;底面的表面溫度14=11℃,84=0.6。試求:
(1)頂棚的總輻射傳熱量;(2)其他3個表面的凈輻射傳熱量。
??
圖9—25 例題9—7附圖
圖9—26 4個灰體表面間的輻射
傳熱等效網絡圖 題解
分析:本題可看作4個灰體表面組成的封閉腔的輻射傳熱問題,其輻射傳熱網絡如圖9—26所示。為了說明網絡法所列出的節點方程與應用計算機求解的有效輻射方程式(9—20)之間的關系,我們先按基爾霍夫定律寫出4個節點的電流方程:
En-J1_J2-J1
J3-J1 J4-J1
=0 1
1
1 3-1
εA A,X1.2 A,X1.3
A,X1.4 EB2-J2
J1-J2 J3-J2 J4-J2
0 1-82
1 1
1 ε2A2
A2X A2X A2X2 2,3
2,4 2.1
Eb3-J3 J1-J3
J2-J3 J4-J
0 1-83
1 1
1 ε3A3
A3X A3X
A3X 3.1
3.2
3.4 Eb4-J4
J1-J4 J2-J4
J3-J4=0 1
1
1 1-84
84A4 AX 專業資料 A.X
A4X43 4,2
把它們改寫成為關于J1~J2代數方程后,有
1
6
b1 -)J1+X12J2+X13J3+X14J4 1-81
I-3 1
-)J2+X23J3+X2,4J4
ε2Eb2 X2,J1-(
1-82
ε2-1 1
ε3Eb3 X31J1+X32J2-(
)J X
十 1-83
ε3-1 X4.1J1+X4.2J2+X43J3-(
1 -)J4
ε4EB4 1-84
ε4-1 顯然,以上4式可統一寫成
4 Ji=ε,σT4-(1-ε;)
Σ JjX i,j
j=1 這就是式(9—20)應用于N=4的情形。
專業資料
計算:各對表面間的角系數可按給定條件求出,其值為X1.2=0.15,X1.3=0.54,X1.4=0.31
X21=0.25,X23=0.50,X2.4=0.25
X3,1=0.27,X3,2=0.14,X3,3=0.32,X3,4=0.27 X4.1=0.31,X4.2=0.15,X4.3=0.54
X1.1=X2.2=X4.4=0 數值求解的結果為:
(1)頂棚的總輻射傳熱量Φ1=1204.5W;
(2)其余3個表面的總輻射傳熱量為Φ2=—395.5W,Φ3=—450.5W,Φ4=-358.5W。
討論:由本例可見,無論是采用網絡法還是采用由式(9—20)所規定的有效輻射顯函數形式的表達式,最終都要求解一組關于有效輻射的代數方程組。而網絡法的主要作用,實質上是給出了列出有效輻射代數方程的一種簡捷方法。
專業資料
例題9—8在直徑為1m、長2m的圓形煙道中,有溫度為1027℃的煙氣通過。若煙氣總壓力為105Pa,其中二氧化碳占10%,水蒸氣占8%,其余為不輻射氣體,試計算煙氣對整個包壁的平均發射率。
題解
分析:為計算氣體對容器整個包壁輻射的平均發射率,首先需要確定相應的平均射線程長,然后按式(9—27)計算。
計算:由表9—3查得平均射線程長
s=0.73d=0.73x1m=0.73mP 于是
PH2oS=0.08x10^Pax0.73m=5.84x103Pa·m
Pcos=0.1x10^Pax0.73m=7.3x103 Pa·m 根據煙氣溫度T=(1027+273)K=1300K及值
PH2OS、PCO2S,分別由圖9-31、 8
9-33查得
H20=0.068,C2=0.092 專業資料
計算參量
(p+PH20)/2=(1+0.08)x105Pa/2=5.4x10+Pa
p=105Pa
PH20(PH20+PCO2)=0.08/(0.08+0.1)=0.444
(PH20+Pco2)S=(0.08+0.1)x10^Pax0.73m=0.131x103Pa·m 分別從圖9—32、9—34、9—35查得
CH20=1.05,Cco2=1.0,Δε=0.014 把以上各值代入式(9—27)得
ε8=1.05x0.068+1.0x0.092-0.014=0.149
討論:由于氣體輻射的容積特性,在論及氣體的發射率時一定要規定氣體所處的容器形狀及對容器的哪一部分而言的發射率,這里是指對整個圓筒體筒身包壁的平均值,近似地選用了短圓柱體的平均射線程長的計算方法。
專業資料
例題9—9若例題9—8中的壁溫tw=527℃,其他條件不變,試確定煙氣對外殼輻射的吸收比。
題解
分析:由于氣體輻射不具備灰體的特性,為計算氣體的吸收比,需要根據容器壁溫與氣體溫度的比值去查取氣體發射率的圖線。上題中已經查到的修正系數
CH20=1.05、Cco2=1.0
仍然可以采用。 計算:計算下列參量:
T
800K PH2OS
=0.0584x105Pa·mx
=3.6x103 Pa·m T
1300K g
T
800K
=4.5x103Pa·m Pco2S
w=0.073x105Pa·mx T
1300K 據這些參量和Tw=800K從圖9—31、9—33分別查得
=0.088,ε
=0.082 0H3
0 于是
0.45
1300K H20=0.088x
=0.109 W6
0.65
1300K αco2=0.082x
=0.112 800K
再據
Tw=800K
PH2o(PH20+PCO2)=0.444
(PH20+PCo2)s=1.31x104Pa·m 在圖9-35上查得
Δα=0.008
于是據式(9—27),氣體吸收比為
α=1.05x0.109+1.0x0.112-0.008=0.219
討論:由例題9—8得 ε=0.149,而對包壁輻射的平均吸收比
αg=0.219,氣體的吸收比還取決于投入輻射表面的溫度。氣體的選擇性吸收及非灰體的特點由此可以清楚的看出。讀者不妨對Tw=1200K的情形重做上述計算,并在計算前估計αg的變化趨向(相當于Tw=800K時的值)。
專業資料
例題9—10 把一燃燒室簡化成直徑為1m、高2m的封閉空間,其平均溫度Tw=800K,燃氣的平均溫度Tg=1300K,8g=0.149,αg=0.219,8w=1。試確定燃氣與燃燒室外殼間的輻射傳熱量。
題解
分析:氣體與燃燒室之間的輻射傳熱簡化成了兩平行平壁組成的封閉系統,其中外壁為黑體,內壁為輻射氣體,如圖9—36所示,可以采用式(9—30)計算單位面積的換熱量。
計算:
Φ=A4=πC(
專業資料
1300K
800K =3.14x1mx2mx5.67W/(㎡·K4)x
0.149x
-0.219x 100
100 =119.6x103W
=119.6kW
討論:式(9—30)的導出采用了兩平行平壁間輻射傳熱的簡化模型,而且其中外壁假定為黑體。如果外壁按灰體處理,就要考慮外壁的多次反射與吸收,計算過程要復雜得多。有興趣的讀者可參見文獻[6,10]。
專業資料
例題9—11 爐膛水冷壁管角系數的確定。
用代數分析法確定圖9—48所示的鍋爐爐膛內火焰對水冷壁的輻射角系數。分析:圖9—48所示已經是從電站鍋爐爐膛中取出的一個模型。為有助于讀者掌握如何從一個復雜的實際問題作出必要的簡化假設后進行理論分析,得出具有一定實際意義的結果這樣一種分析問題的方法,下面從鍋爐爐膛開始將一步一步的簡化過程出示于圖9—49中。
首先,因為垂直于紙面方向管長較管距大得多,可以從三維的爐膛取出一個截面加以研究,對一個截面又可以取出一面爐墻為代表;火焰輻射能只有通過與排管相切的假想平面K—K才能到達水冷壁管排和爐墻,因此可把K—K平面作為火焰輻射面;同一面墻上可以取相鄰兩根管子為代表;再利用對稱性,最后可以把問題簡化為三表面的模型來討論。顯然,表面 AD、AMB以及BCD構成了3個非凹形表面組成的封閉系統。所謂火焰對水冷壁管的角系數,即平面AD對凸表面AMB的角系數。這樣就可直接用式(9—8)計算火焰對水冷壁管的角系數X。
專業資料 爐墻
火焰輻射 圖9-48
分析火焰對水冷壁 角系數的圖示 8000000
以假想面K-K
000000 簡化為二維
面墻為代表
代替煙氣
火焰和煙氣 取相鄰兩根管
?
三表面問題 為代表
圖9—49 計算鍋爐爐膛火焰對水冷壁管角系數的模型
計算:
AD+AMB-BCD AD+AMB-BCD X=2
2AD
AD
其中AD=s,AM=CD(幾何對稱),將這些關系代入上式得
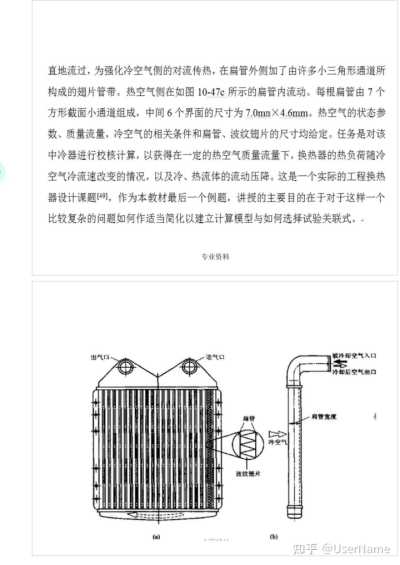
AM+MB+s-BC-CD MB+s-BC X=2
因為
BC=(s2-d2)12 MB=ad α=arccos(d/s)
1/2 所以
(%)-]-(/p)s000+1=x
討論:這是對實際工程問題作一定的簡化假設從而得出有用的分析結果的又一個例子。工程實際應用中要得出的是水冷壁管從火焰及爐墻所得到的總的輻射能量。由于爐膛本身的溫度相對火焰來說要低得多,因而可以不予考慮,只要考慮火焰輻射落到爐墻上的部分中被反射回來又落到水冷壁管上的
專業資料
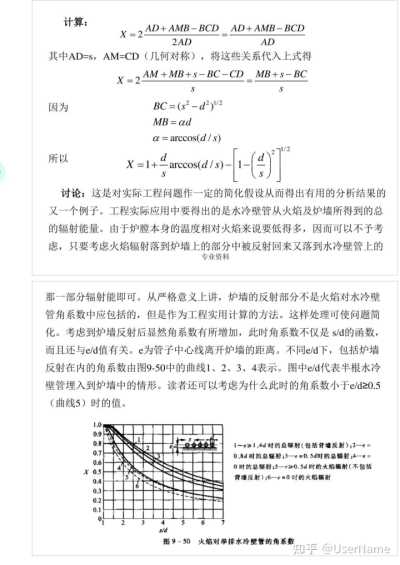
那一部分輻射能即可。從嚴格意義上講,爐墻的反射部分不是火焰對水冷壁管角系數中應包括的,但是作為工程實用計算的方法。這樣處理可使問題簡化。考慮到爐墻反射后顯然角系數有所增加,此時角系數不僅是s/d的函數,而且還與e/d值有關。e為管子中心線離開爐墻的距離。不同e/d下,包括爐墻反射在內的角系數由圖9—50中的曲線1、2、3、4表示。圖中e/d代表半根水冷壁管埋入到爐墻中的情形。讀者還可以考慮為什么此時的角系數小于e/d≥0.5(曲線5)時的值。
1.0 60 1 0.8
1—e≥1,4d時的總輻射(包括背墻反射);2—e=0.7
0,8d時的總輻射;3—e=0.5d時的總輻射;4—e=0.6
0時的總輻射:5—e≥0.5d時的火焰輻射(不包括X 0.5
0.4
背墻反射);6—e=0時的火焰輻射0.3
0.2 0.1 0 2 3 4 5 6 s/d
圖9—50 火焰對單排水冷壁管的角系數
例題9—12 太陽能集熱器的熱計算。
有一個平板型太陽能集熱器如圖9—51所示。已知:包括散射輻射在內的投入太陽能輻射為750W/㎡;透明覆蓋采用厚δ=0.9mm的普通玻璃,吸熱面采用銅材,其上鍍有8x10—6mg/㎡的光譜選擇性涂層黑鎳,實驗測得吸熱面的平均溫度為90℃,覆蓋玻璃內表面的平均溫度t=50℃,吸熱面與覆蓋玻璃間的距離為4cm。玻璃對太陽能的穿透比取
G, 為τ=0.90(參見圖8—21),吸熱面對太陽
- 能的吸收比a=0.93(參見表9—4)。吸熱
2- 面自身發射率ε=0.094(參見表9—4),
SIGNAT
5 覆蓋玻璃發射率ε=0.94(參見表8—2)。
試確定該太陽能集熱器單位面積的有效
冷卻水流過 吸熱量以及集熱器的效率。
圖9—51 平板型太陽能集熱器1一透明覆蓋;2一吸熱面;
3—金屬管:4—絕熱材料;5—箱體專業資料
題解
分析:這是一個復雜的熱量傳遞過程:太陽的投入輻射G,到達覆蓋玻璃上時,一部分穿透玻璃(取決于玻璃穿透比τ)穿透部分抵達吸熱面上時,其中的α,部分被吸收,其余則反射并透過覆蓋玻璃抵達外界;由于吸熱面的溫度高于覆蓋玻璃的溫度,因此這兩塊平行板之間有輻射傳熱,設單位面積的輻射傳熱量為q,.p,同時吸熱面與空腔中的空氣之間還有對流傳熱,設換熱量為qrco因此對集熱器吸熱面而言,單位面積上凈得到的熱流密度qc1,可表示為
qd=tG,a,-qr.p-9c.p
(9-35) 其中吸熱面與覆蓋玻璃內表面間的輻射傳熱可以應用式(9—16)計算,即
qr.p
1 1 + -1 "3 "3 專業資料
-
- -
式(9—35)中的qc,p可按平行夾層的有限空間自然對流關聯式,即式(6—47),計算。所謂集熱器的效率就是下列比值:
(9-36) Pb
、
G
計算:先計算自然對流散熱量。定性溫度
trr+tp
(50+90)℃
=70℃。 1
2
2 空氣的有關物性為:
λ=2.96x102W/(m·K),v=20.02x10-6㎡/s,Pr=0.694
9.8m/s2x
1
-x(90-50)℃x(0.04m)3 gaΔtoPr
343K
x0.694=126649 Gr Pr=
v2
(20.02x106㎡/s)2 據式(6—19a)有
Nu=0.212x(GrPr)14=0.212x(126649)14=4.0 Nuλ
h=
=4.0x0.0296W/(m·K)/0.04m=2.96W/(㎡2·K) δ
qcp=hΔt=2.96W/(m·K)x40℃=118W/㎡
專業資料
再計算輻射散熱量。
5.67W/(㎡·K4)x
363
(323)k 001
qr.p
81.7W/㎡ 1
1 I +
0.09 0.94 所以集熱器的有效熱流密度為
qa=0.90x750W/㎡x0.93-118.0W/㎡-81.7W/㎡=428.1W/㎡ 428.1W/㎡
n
=57.1%
750W/㎡
討論:這一集熱器的效率是不算低的。究其原因,除了采用選擇性涂層外吸熱板上覆蓋一層玻璃也是重要因素,這不僅利用了溫室效應,而且減少了表面的對流散熱損失。從上述計算可見,自然對流散熱損失是一項主要的損失。要進一步提高效率,可以在吸熱表面與玻璃蓋板之間堆放一些對太陽光透明的材料,例如玻璃管,以抑制夾層中的自然對流。如果自然對流能完
專業資料
全抑制,夾層中為全空氣導熱,則吸熱面的這一散熱在理想情況下可減少到
λΔt
0.0296W/(m·K)x40℃ qc.p=
δ
0.04m
=29.6W/㎡ 此時,集熱器效率可提高到
(750x0.9x0.93-118-29.6)W/m
480.1
=64% u
2 750W/m
750 有關太陽能利用方面的更多的傳熱學問題可參見文獻[13]
專業資料
例題9—13 空間輻射制冷器工作原理分析。
當航天器在太空中飛行時,航天器內部電子儀器和設備的發熱量必須通過航天器外殼與太空間的輻射傳熱散發出去,這時可以完全不考慮星星對航天器的反射,并且可以認為宇宙是一個0K的黑體,完全吸收了航天器的熱輻射。當電子器件本身的發熱值很小時,例如幾十毫瓦的級別,可以采用所謂的輻射制冷器來冷卻器件。圖
φ302mm
外輻射器 9—52中所示是一個輻射制冷器
的截面圖[13],其中探測器就是
室溫支架 發熱的元件(被冷卻對象)。
多層隔熱材料 試分析輻射制冷器的冷卻原理。
內輻射器 隔熱支架
ф117mm 圖9-52
輻射制冷器示意圖 マ業貝
71mm 85mm
題解
分析:現考慮將發熱元件簡單地暴露于宇宙空間中的情形。假設它沒有得到來自其他方面的熱量,則達到熱平衡時,器件向宇宙空間的輻射散熱等于其發熱量,即有
Φ εσT4
A
式中A為器件的散熱面積,Φis為內熱源功率。對一個功率為50mW的元件,如果其散熱表面的直徑為95mm,發射率為0.9,則此時的平衡溫度為
50x10-3W
=77K r=
3.14x(0.095m)2x0.9x5.67x10-8W/(㎡·K4)
所以低熱耗的電子元件可以暴露于宇宙空間中通過直接輻射而達到被冷卻的目的,這就是輻射制冷器的最基本的工作原理。
要進一步提高輻射制冷器的效率,需要采取多種完善措施。對圖9—52所示的結構來分析。該制冷器采用了以資價措施來改進性能:
(1)采用錐形屏蔽罩(即遮熱罩)來遮擋從航天器其他部位發出的熱輻射,同時又基本不會阻擋電子元件向宇宙空間輻射的散熱。當然,錐角的大小與該元件在航天器上的位置有關,需要通過具體的計算來確定。
(2)在屏蔽罩的錐角開口處,增加了一個外輻射器。這是一個中間透空的圓環,其作用是將通過制冷器的骨架、連接構件從航天器來的雜散熱量能向太空發射出去。
(3)為進一步減少從航天器本身傳遞過來的熱量,輻射制冷器的外殼敷設了多層抽真空的隔熱保溫材料。
根據文獻[14],圖9—52是專門為100K以下排散10mW熱量的器件設計的輻射制冷器,內輻射器的直徑為10cm,輻射表面的a,=0.08、ε=0.8,屏蔽罩的α,=0.1、ε=0.02,總重約為1.6kg。有關輻射制冷器的更多內容可參見文獻[14,15]。
專業資料
例題10—1 蒸汽管道的外徑為80mm,壁厚3mm,外側包有厚40mm的水泥珍珠巖保溫層,其導熱系數{12)w(mK)
=0.0651+0.000105{f}c(T為保溫層的平均溫度)。管內蒸汽溫度tn=150℃,環境溫度t。=20℃,保溫層外表面對環境的復合表面傳熱系數h。=7.6W/(㎡2.K),管內蒸汽的表面傳熱系數h;=116W/(㎡2.K),鋼管壁的λ=46.2W/(m·K)。求每米管長的熱損失。
題解
分析:這道題的難點是水泥珍珠巖的導熱系數入與其兩個表面的溫度有關,這兩個溫度預先并不知道,而是求解的結果。為了進行計算需要預先假定。保溫層的內表面溫度可以看成與管內的蒸汽溫度相同,因為管內對流熱阻和管壁的導熱熱阻都很小(從下面的數值對比中可以清楚地看到這一點)。保溫層外表面的溫度可以先假設為30℃,以后再修正。經過數次迭代計算,就可以得到滿足一定要求的結果這種“要求解什么需要假設什么”的問題就是
一種典型的非線性問題。對于非線性問題,迭代法是一種行之有效的求解方
專業資料
法。
計算:保溫層外徑
d。=80x103m+40x10-3mx2=0.16m 每米管長的熱損失
Φ=kπdl(tj-t )=kπx0.16mx1mx(150℃-20℃)=65.3k ㎡.℃ 管道內徑
d;=80x10-3m-3x10-3mx2=0.074m 由式(10-4)得
1
0.16m
0.16m
0.08 k=1/
xln
+ 116W/(㎡.℃) 0.074m
2x46.2W/(m·K)
0.074 0.16m
0.16m
1 In
+ 2π2
0.08m 7.6W/(㎡·K) 保溫層的平均溫度
1
t=-x(150℃+30℃)=90℃ 2
專業資料
于是
■2=(0.0651+0.000105x90)W/(m·K)=0.0746W/(m·K) 代入上式得
1 k=
W/(㎡2·K)=1.119W/(㎡·K) 0.0186+0.0000675+0.743+0.132
從分母中四項熱阻的對比來看,管內對流熱阻和管壁的導熱熱阻均很小,特別是管壁熱阻,完全可以忽略不計。這說明,將保溫層內表面的溫度取作150℃是完全允許的。于是,每米管長的熱損失為
Φ=65.3㎡2.℃x1.119W/(㎡2.K)=73.1K
這還不是最后的答案,因為保溫層的外表面溫度30℃是帶有假設性的,需要加以校核。外表面溫度可按下式計算:
Φ
73.1W +20℃=
+20℃=39.1℃ πd。h。
πx0.16mx7.6W/(㎡·K)
專業資料
再依次作為保溫層外表面溫度,重新計算:
150+39.1 2=0.0651+0.000105x
W/(m·K)=0.0750W/(m·K) 2
k=1.124W/(㎡·K),Φ=73.4W
討論:(1)對于輸送水或壓力較高的水蒸氣的保溫管道,管內介質的對流傳熱阻力一般比保溫層的熱阻要小得多,因而常可取管壁溫度高于管內介質的平均溫度,這種做法對于工程傳熱問題的簡捷分析特別有用。
(2)由于導熱系數是溫度的函數,計算過程必是迭代性的。本例兩次相鄰計算中保溫材料導熱系數的相對偏差已小于1%,作為工程計算可以認為迭代也已收斂。
專業資料
例題10—2 鋁電線外徑為5.1mm,外包導熱系數λ=0.15W/(m·K)的聚氯乙烯作為絕緣層。環境溫度為40℃,鋁線表面溫度限制在70℃以下。絕緣層表面與環境間的復合表面傳熱系數為10W/(㎡2·K)。求絕緣層厚度δ不同時每米電線的散熱量。
題解
分析:像式(10—2)這樣確定所傳遞熱量的計算式可以進一步拓寬應用:只要分子上的溫差與分母中的熱阻對應即可。對于本題,給定了電線表面溫度的數值,相當于圖10—2中的t,環境溫度相當于圖中的tro,因此每米長電線的散熱量為:
π(tmi-t) Φ
l 1 d 1 In 0 + 2λ
d; hod。
專業資料 計算:將已知條件代入上式,得
Φ
πx(70℃-40℃) l
1
1 °p
xln 2x0.15W/(m·K)
0.0051m 10W/(㎡·K)d。 Φ
是絕緣層外徑(即絕緣層厚度)的函數。取d。為10~70mm,計算結果用圖1
線表示于圖10—4。圖中橫坐標為絕緣層外徑d。,縱坐標分別表征絕緣層導熱熱阻的
1
In(d。/d)、表征絕緣層外側熱阻的
1 和散熱量
1/0 2λ
hod。 11
3 10
10 6
2 6
5 0 10 20 30 40
50 60 70 80
djmm
圖10—4 電線散熱量與絕緣層外徑的關系
1/m/或//(m·K/w) (Φlty(W/m)
討論:從上圖可以看出:d。=30mm時散熱量達到最大值,而當絕緣層外徑小于30mm時,增加絕緣層厚度非但不會削弱傳熱,反而會增加散熱。對電線來說,處于這種情況下是有利的,因為可以增加電流的通過能力。本題所述電線的實際產品所采用的絕緣層厚度約為1mm,處于對散熱有利的范圍內。
專業資料
例題10—3對一臺冷油器進行傳熱試驗得到下列參數:進口油溫t1'=49.9℃,進口水溫t2'=21.4℃。出口油溫t1”=44.6℃。出口水溫t2”=24℃;水的質量流量qm=21.5x103kg/h;傳熱面積A=2.85㎡。冷、熱流體的流動方向相反。試計算該工況下冷油器的平均溫差。
題解
分析:以下計算中認為推導平均溫差的假設均成立。
據題意,油和水的溫度的沿程變化如圖10—29中的實線所示。此時有
Δtmax=49.9℃-24℃=25.9℃
Δt...=44.6℃C-21.4℃=23.2℃ Δtmax
25.9℃ =1.116<2 23.2℃
Δtmin 所以可以采用算術平均溫差。
專業資料
1/℃
油
49.9 44.6
24 21.4
0
圖10—29 例題10—3圖示和分析計算:
Δt Δt
25.9℃C+23.2℃ x
Δt max min
=24.6℃C 公
2
2
討論:圖10—29中用實線示出了本題冷、熱流體的溫度變化曲線。試問,本題中的溫度曲線可否畫成如圖中虛線所示?為什么圖10—21中逆流的溫度分布曲線畫成了向上凸的形式?
專業資料
例題 10—4 在一個螺旋式換熱器(圖 10—12)中,熱水流量為2000kg/h,冷水流量為3000kg/h;熱水進口溫度t1=80℃,冷水進口溫度t'2=10℃。如果要求將冷水加熱到t”2=30℃,試求順流和逆流時的平均溫差。
題解
分析:首先應根據熱平衡關系算出熱流體的出口溫度,然后按照順流與逆流的方式布置,計算相應的平均溫度。
計算:9mG(t'1-t"1)=qm2c2(t"2-t'2)
在本題給定溫度范圍內,水的比熱容c1=c2=4200J/(kg.K)。代入上式:(2000/3600)kg/sx(80℃-t")=(3000/3600)kg/sx(30℃-10℃)
專業資料
得
t"1=50℃
(1)順流時,Δmax=80℃-10℃=70℃,Δmin=50℃-30℃=20℃,代入 (10-11)得
Δ
70℃-20℃
=39.9℃ 多
1n 70℃
20℃
(2)逆流時 Δmax=80℃-30℃=50℃,Δmin=50℃-10℃=40℃,代入 (10-11)得
50℃-40℃=44.8℃ Δt
m
50℃ ?
40℃
討論:逆流布置時Δtm比順流時大12.3%。也就是說,在同樣的傳熱量和同樣的傳熱系數下,只要將順流系統改成逆流系統,就可以減少12.3%的換熱面積。
π入
例題10—5上例中,如改用1—2型殼管式換熱器,冷水走殼程,熱水走管程,求平均溫差。
題解
分析:這里把參數P、R計算中的下標1、2分別看成是殼側與管側。計算:
P= t"2-t'2_
50℃-80℃
=0.428 t'1-t'2
10℃-80℃ t'1-t"1
10℃-30℃
=0.667 R=
t"2-t'2
50℃-80℃ 由圖10—23查的Φ=0.95。
上例中已求得逆流時平均溫差為44.88℃。于是,1—2型殼管式換熱器中的平均溫差為
Δm=0.95x44.8℃=42.6℃
討論:如果讓冷水走管程,熱水走殼程,則有。
P=
t"2-t'2。
30℃-10℃
=0.286 t'1-t'2
80°C-10℃ t'1-t"1
80℃-50℃
=1.50 R=
t"2-t'2
30℃-10℃
由圖10—23仍得=0.95。而且還可以發現,這里的P值即為上述計算中的PR,而此處的R則為上述計算中的1/R。可見在P、R的定義式(10—13)中,下標1、2 僅是指兩種流體,對于殼管式換熱器沒有必要一定要把下標1、2與殼側、管側(或熱流體,冷流體)對應起來,對交叉流換熱器也沒有必要一定要把下標1、2與流體的冷、熱(或混合不混合)聯系起來。本書前面對下標1、2的說明僅是為便于教學而已。
專業資料
例題10—6流量為39m3/h的30號透平油,在冷油器中從t'1=56.9℃冷卻到t”1=45℃。冷油器采用1—2型殼管式結構,管子為銅管,外徑為15mm,壁厚1mm。每小時47.7t的河水作為冷卻水在管側流過,進口溫度為t2=33℃。油安排在殼側。油側的表面傳熱系數h。=450W/(㎡2.K),水側表面傳熱系數hi=5850 W/(㎡2.K)。已知30號透平油在運行溫度下的物性為p1=879kg/m3,c1=1.95kJ/(kg.K)。試求所需傳熱面積。
題解
分析:本題是一個設計計算,換熱量可以從油側得出,根據熱平衡關系,計算出水的出口溫度,進而得出對數平均溫差。在計算傳熱系數時,要明確是以那一側面積為依據,如果以外側為依據,利用式(10—25),內側的污垢熱阻也要考慮到面積比的影響。
計算:油側的體積流量為
專業資料
39m3
=1.083x10-2m3/s qv1
3600s 油側的熱流量為
Φ=qmG(t'1-t"1)=quP1G(t'1-t"1)
=1.083x10-2m3/sx879kg/m3x1.95kJ/(kg.K)x(56.9℃-45℃) =2.21x105W
水側的質量流量為
47.7x103kg
=13.25kg/s qm2
3600s 冷卻水的溫升。
專業資料
2.21x103W Φ
=4℃。 t"2-t'2=
13.25kg/sx4.19x103J/(kg.K) b
于是冷卻水的出口溫度為
t"2=33℃+4℃=37℃ 參量P和R為
P= t"2-t'2
37℃C-33℃
=0.17 t'1-t'2
56.9℃C-33℃ t'1-t"1
56.9℃-45℃
=3 R=
t"2-t'2
37℃C-33℃ 查圖10—23得=0.97。對數平均溫差為
專業資料
Δm=0.97x
(56.9℃-37℃C)-(45℃-33℃)
=15.1℃ 56.9℃-37℃
1n
45℃-33℃
按表10—1分別取管內、外側污垢熱阻為0.0005㎡.K/W和0.0002㎡.K/W,于是傳熱系數(略去管壁導熱阻力)為
1
A。 k
R。+(R+-
1 rac{1}{60
h'A
5850W/(㎡.K) 1
1
+0.0005㎡.K/W)x
15 +0.0002㎡.K/W+(
= 1/
450W/(㎡.K)
13 =313W/(㎡.K)
冷油器的計算面積為
專業資料
2.21x105W Φ
46.8㎡ A=
313W/(㎡.K)x15.1℃ kΔt,
實際設計面積可留10%的裕度,取為46.8x1.10㎡=51.5㎡。
討論:雖然在熱計算中已計及了污垢熱阻(占總熱阻的1/4以上),但在決定實際換熱量面積時又加了10%的冗余面積,以照顧到某些未計及的因素(例如獲得傳熱系數時可能的誤差等)。
例題10—7 上例中,如冷油器的進口溫度變為58.7℃,而水的流量、進口溫度以及油的流量均不變,求出口油溫和出口水溫。
題解
分析:換熱器運行中經常會發生運行條件的變化,成為變工況,進口溫度的變化是一種可能的變工況。油和水的溫度如升高很多,則需考慮物性變化對k的影響。現在變化甚少,可以認為傳熱系數仍為313W/(㎡2.K)。此題應采用s—NTU
專業貝科
法計算。
計算:
qmq=1.083x102m3/sx879kg/mx1.95x103J(kg.K) =1.856x104W/K
qm2C2=13.25kg/sx4.19x103J/(kg.K)=5.552x102w/K
(qmc)min
1.856x104W/K
=0.334 (qmC)max
5.552x104W/K kA
313x51.5W/K NTU=
=0.87 (qmc)min
1.856x104W/K 查圖10—32得ε=0.54。熱流量可按式(10—17)算出:
專業資料
①=s(qmc)mn(t1-t'2)
=0.54x1.856x10+W/Kx(58.7℃-33℃) =2.58x105W
由熱平衡式可求得油和水的出口溫度
Φ
2.58x105W t"1=t'1--
=(58.7℃
)=44.8℃ 1.856x10+W/K
bub Φ
2.58x105W t"2=t'2+-
-=(33℃+
5.552x10+W/K
)=37.6℃ qm2C2
專業資料
討論:這一題目是采用傳熱單元數法優于平均溫度法的典型。如果采用后者,需先假定t”(或t”2),然后從傳熱方程及熱平衡方程計算出的熱量是否相符來判斷所假設之值是否正確。還應指出,由于t1的變化很小(約為熱流體溫降的15%),因而兩種計算的熱量必須符合得較好才能得出合理的結果。
例題10—8 有一臺空氣冷卻器,空氣在管外垂直流過管束,ho=90W/(㎡2.K);冷卻水在管內流動,h=6000W/(㎡.K);換熱管為外徑16mm,厚1.5mm的黃銅管。求:(1)空氣冷卻器的傳熱系數;(2)如果h。增加1倍,傳熱系數如如何變化?(3)如果h增加1倍,傳熱系數如何變化?
題解
分析:黃銅的導熱系數由書末的附錄查取,為111W/(m.K)。空氣在管外流動,應是主要熱阻所在,所以以外表面積作為計算面積。
專業資料 計算(1)由式(10—4)得
1 k=
1
16mm
0.016m
16
1 十
ln(
一)+ x
6000W/(㎡.K) 13mm 2x111W/(m.K)
13
(Xw)/M06 1
W/(㎡.K) 0.000205+0.0000149+0.0111 =88.3W(㎡K)
(2)
由以上計算可見,管壁熱阻要比管內熱阻小兩個以上的數量級,可以略去不計,于是有。
1 k=
=174W/(㎡.K)。 0.000205+0.0111
傳熱系數增加了96%。(3)
k= 1
W/(㎡.K)=89.3W/(㎡.K) 1
16 x-+0.0111 12000 13
專業資料
傳熱系數的增加不到1%。
討論:本例的計算表明:要強化一個傳熱過程,必須首先比較各個環節的熱阻,找出分熱阻最大的環節,并采用強化傳熱技術減小其熱阻值,才能收到效果。
例題10—9 蒸汽再熱器內肋片管作用分析[48]。
近代高參數大容量火力發電廠常采用蒸汽再熱循環以提高熱經濟性,即把在汽輪機高壓缸中作過功的蒸汽重新送入鍋爐加熱到高溫,然后返回汽輪機的中、低壓缸。再熱蒸汽壓力一般為2~3MPa,流經再熱器的蒸汽流速受到其壓降(不大于自身壓力的8%~10%)的限制。較小的流速及較低的壓力都使再熱器中蒸汽側的表面傳熱系數下降。如果把再熱器布置到煙道中煙氣溫度較高的區域(圖10—46a),就可能會因壁溫過高而需采用昂貴的奧氏體鋼;如把它布置到煙氣溫度較低的區域,則因平均溫壓下降使所需的傳熱面積增大,對經濟性及運行特性均不利。這就是在設計與布置再熱器時所遇到的一對矛盾。
專業資料 采用內肋管有可能將
再熱器移到高溫煙氣區屏
(B)
(b) 專業資料
對流過熱器 再熱器
x
x 50
x
x x x
光管 40
一0
肋片管 o 。
8 30
0 0
7.1
20 肋片管截面圖
70 80 90
100% 相對負荷
(c)
(d) 圖10—46 蒸汽再熱器內肋片管示意圖
分-入
在再熱器中高溫煙氣在管外橫向沖刷管束,面被加熱的蒸汽在管內流動,蒸汽是“冷”流體。要降低壁溫就應使管壁溫度盡量接近于蒸汽溫度。為此可以考慮在蒸汽側裝肋片以降低蒸汽側的熱阻。為加工方便可采用縱向內肋片管(圖10-46b、c)。
試對于圖10—46所示的情形,確定采用縱向內肋片管的再熱器與光管再熱器在蒸汽出口處管壁溫度與蒸汽溫度之差的比。
題解
分析:假設:(1)兩個再熱器的外形尺寸(包括煙氣側的換熱面積)相同;(2)蒸汽參數(質量流量、進出口溫度及壓力)相同;(3)煙氣參數(流速、溫度、煙氣成分及壓力)相同;(4)管壁熱阻可以不計;定義縱向肋片管管壁溫度、光管管壁溫度與蒸汽間的溫度差為
專業資料 A/C
Le=-tΔsm=1sm-
(a), 其中,t及tsm分別為縱向內肋片管平均壁溫及光管平均壁溫,t為再熱蒸
汽溫度。
用Acu、Acsm和Pu、Psm分別表示兩種管子的蒸汽流動截面面積及周界長度,對于蒸汽側可寫出
hsmPsmAsm=hgPLΔtt。 即
ΔtLs hsm Psm Δt hmPLf
(b). Sm
專業資料 計算:據式(6—15)有
h=B (pw)08
0.8 P 0.2
B9m 200
402Ac
其中,qm為再熱器中通過每根管子的質量流量,B為由有關物性組成的綜合量。
按比較條件,兩種再熱器的B及qm各自相等,因而有。
hsm=
0.2 () PLf
(c)。 sy
將式(c)代入式(b)可得
Δ/Lt (55m Pe
(A) Nsm
專業資料
由于Psm<Bu、Au<As,因而ΔtL<Δtsm。這就是說,內肋片管起到了降低壁溫的作用。在文獻[48]中介紹了光管再熱器及內肋片管再熱器工業性對比試驗的結果。對比試驗在一臺280x103kg/h的超高壓直流鍋爐上進行。所用內肋片管的截面尺寸(圖10—46c)所示。將有關數值代入式(d)得
tre-ty_
152.3mm 12
1622m㎡
=0.63 tsm-t
199.6mm
1847mm
(e)。
討論:試驗測得的這兩個溫差的比值約為0.65(圖10—46d),可見上述簡單的理論分析與實驗結果相符甚好。在所試驗的鍋爐中,有肋片的再熱器的平均壁溫比光管再熱器低約20℃左右。
本例中,由于主要熱阻是在煙氣側,蒸汽側加翅片并不能強化傳熱,而主要是改變壁面溫度的工況,因此可以假定光管與翅片管傳熱量相同,蒸汽側、煙氣側的參數都一樣。
專業資料
本例的分析揭示了翅片(肋片)的另一個重要作用:翅片能使壁面溫度更接近同側流體的溫度,當該側流體是換熱器中的低溫流體時,可有效地降低金屬表面溫度。
例題10—10 增壓內燃機用空氣中冷器熱設計。
為提高汽車動力、節油降耗及降低汽車排放污染物,在增壓內燃機車上增加空氣中間冷卻器(簡稱中冷器)是個有效措施。中冷器可以使增壓后的空氣溫度降低,密度增大。增壓中冷可以在柴油機的熱負荷不增加甚至降低以及機械負荷增加不多的前提下,較大幅度地提高柴油機功率,降低排放污染。因此,在增壓內燃機車上高效中冷器的利用對于節約能源,保護環境具有重要意義。
所計算的中冷器示于圖10—47中。增壓后的熱空氣先流經由若干根扁管構成的第一通路,后在接頭管道中轉彎進入第二通路,冷空氣則在扁管間的空間中垂
專業資料
直地流過,為強化冷空氣側的對流傳熱,在扁管外側加了由許多小三角形通道所構成的翅片管帶。熱空氣側在如圖10—47c所示的扁管內流動。每根扁管由7個方形截面小通道組成,中間6個界面的尺寸為7.0mmx4.6mm。熱空氣的狀態參數、質量流量,冷空氣的相關條件和扁管、波紋翅片的尺寸均給定。任務是對該中冷器進行校核計算,以獲得在一定的熱空氣質量流量下,換熱器的熱負荷隨冷空氣冷流速改變的情況,以及冷、熱流體的流動壓降。這是一個實際的工程換熱器設計課題[49],作為本教材最后一個例題,講授的主要目的在于對于這樣一個比較復雜的問題如何作適當簡化以建立計算模型與如何選擇試驗關聯式。
專業資料 出氣口
進氣口
被冷卻空氣入口
冷卻后空氣出口 扁管
扁管寬度
3 波紋翅片
000003E
(c)
圖10—47 管帶式柴油機中冷器題解
分明:對所計算的換熱器進行以下三方面的分析。
(1)物理問題的簡化假設。從冷、熱流體流動過程中的混合情形而言,本換熱器屬于兩種流體均各自不混合的情形;冷、熱流體流過的通道截面形狀均非圓形,對冷流體流動方向通道的長度與通道的當量直徑之比小于流動進入充分發展所需之值。熱流體的換熱是在兩個串接的換熱單元中完成的。上述特點給計算
專業資料
帶來一定的困難,經過分析采用以下處理方法:1)考慮到熱流體在接頭通道中并沒有充分混合,因此將第一與第二通道串聯起來當作一個長通道考慮。2)在一般的文獻中對數平均溫差計算式中的修正系數均用圖線給出,不能適應計算機編程的需要,這里直接從文獻[50]的無窮級數計算式出發來獲得兩種流體均不混合的對數平均溫差修正系數計算的解析表達式。3)假設在各根扁管中流量均勻分配,每根扁管的流動與傳熱情況都一樣,可以取出一根扁管作為分析對象;對于非圓形截面的流動,考慮到大多數計算工況均為湍流,采用當量直徑作為傳熱與阻力關聯式的特征尺度。4)作為管內流體的通道取出扁管中的一個通路來考慮,該通路上下壁面的外側為翅片,左右壁面是分隔壁的一半。5)由翅片構成的三角形通道分為上下兩半,分別屬于兩個相鄰的扁管。而每個扁管上下表面各有半個三角形通道,相當于一個完整的三角形通道。扁管翅片的肋效率按等截面直肋公式計算。由于肋效率與換熱系數有關,因此肋效率的值需在求解過程中動
專業資料
態地決定。
經過上述簡化處理,所研究的換熱器的計算模型如圖10—48所示。(2)計算公式選擇。內表面為計算依據,k的計算如下式:
1
(a) k=
1+R+S+1+ h
λ A。h。 A。 式中:h、h。_管子內外對流傳熱表面傳熱系數;
Ai、Ao_扁管內外換熱面積;
Ri、Ro_扁管內外的污垢熱阻,根據表 10—2和運行經驗取為0.0002m2.k/W;
8_管壁的厚度;
λ_管壁的導熱系數。
專業資料
翅片
冷空氣 扁管
翅片 計算單元寬度
圖10-48
中冷器的計算模型
Nuλ
h=
p 管子內、外對流表面傳熱傳熱系數h由Nu數確定,即:
,其 中:λg為管內外流體的導熱系數;de為通道的當量直徑。
1)管外側Nu的確定。冷空氣在三角形截面的短通道內流動與換熱,根據Re數的大小分別按以下公式計算:
①Re≤2300時采用Sieder-Tate公式計算,見式(6-26); ②Re>2300時按Gnielinski公式計算,見式(6-21)。
2)管內側Nu的確定。管內側流體傳熱系數按Gnielinski 公式計算。管內外流體的阻力系數均按
f=(1.821g Re-1.64)-2
(b) 計算,得出阻力系數后,按
(c) ΔD=1/2pu2/4
計算壓降。
(3)換熱面積確定。確定換熱面積的基本思想如下:1)按照圖10—47c,把扁管分成八根小通道,認為每一根小通道內的換熱情形都一樣,以一根小通道為計算單位,A1為第一個小通道的內表面面積,按實際尺寸計算。2)管外側將翹片按圖10—47所示處理,外表面計算面積A。由下式算出
Ao=A,+7jA,
(P)
式中:A為管子根部面積,Ar為肋片面積,n為肋效率。3)肋效率n4的確定:按等截面直肋公式(2—43)計算,該式中的空氣對數傳熱系數需在計算中確定。
專業資料
計算:顯然這樣的計算必須借助計算機來完成。為節省篇幅具體計算細節這里不予列出,有興趣的讀者可參見文獻[49]。
討論:在不同迎面風速下中冷器的熱負荷的計算值與實測值與風速的關系示于圖10—49a,圖10—49b給出了冷空氣側壓降計算值與實測值的比較,由圖可見,上述計算模型的預測值與實驗值結果符合較好。
本章所提供的兩個例題都是從工程實際問題中摘選出來的。這兩個例題說明,在本課程內容學習的基礎上,對較為復雜的傳熱問題,通過必要而合理的簡化假設(需要一定的實踐經驗),可以得出具有相當準確性的工程預測計算。讀者在學習本課程時,要努力掌握這種對實際問題進行一定的簡化、建立計算模型、運用已經掌握的知識而獲得具有一定應用價值結果的方法。
專業資料
01
8 2 0
1 5 15 20 25 30 35
40 01
質量流速/[kg/(m·s)](a)換熱量隨冷空氣速度的變化
檢號
''1111
12
2422086 換熱量/W
400 350- 300- 250- 200- 150- 100 S0 0 5 10 15 20 25 30 35
40 空氣質量流速/[kg/(m·s)]
(b)冷空氣壓降隨流速的變化
圖10—49 計算值與實驗值的對比專業資料
例題11—1直徑為10mm的量筒底部的水層向空氣中擴散。水面至量筒口的高度為150mm,量筒口處的大氣為干空氣,整個系統處于25℃的條件下。試計算水的蒸發率。
題解
分析:可用式(11—9)求質量通量密度。由附錄知D=0.256x10+㎡2/s。水蒸氣在量筒底面水層上的分壓力為25℃下的飽和壓力,由詳細的水蒸氣表(見文獻[5]第456頁)查出為pw1=0.0317x105Pa。量筒口味干空氣,pwx2=0。
計算:
Pa=P。-Pm1=(1.0132-0.0317)x105Pa=0.9815x105Pa. Pa2=P。-Pw2=(1.0132-0)x10^Pa=1.0132x10^Pa.
專業資料
阻力/Pa
Dp。1
1n Pa2
0.256x10-㎡/sx1.0132x105Pa
xln
1.0132x105Pa Mw=RIA
Pa1
㎡/(s2.K)x298Kx0.15m 8314
0.9815x105Pa 18
=3.99x10-6kg/(㎡s)
蒸發率=M.A=3.99x10-0kg/(㎡2.s)x3.14x(5x10-3m) =3.13x10-10kg/s
討論:如果用精密的天平測定在一定時間間隔內量筒中液體的蒸發率,則可由式(11—9)來確定該液體的蒸氣在空氣中的擴散系數。
例題11—2 含少量碘的壓力為1.013x105Pa、溫度為25℃的空氣,以5.18m/s的速度流過直徑為3.05x10—2m的圓管。設在空氣流中碘蒸氣的平均物質的量濃度為cm,管壁表面碘蒸氣的濃度為零,試確定從氣流到管壁的傳質系數及碘蒸氣在管子表面的沉積率。空氣—碘的質擴散率D=0.826x105㎡2/s(p=1.013x105Pa,
t=25℃)。
題解
假設:忽略碘蒸氣對氣流物性的影響,可從空氣的物性表查得物性參數;假定過程已經穩定。
計算:查得空氣的v=15.53x10—6m2/s。于是有。
ud 5.18m/sx3.05x10-2m Re=
=1.02x10+ v
15.53x10-6㎡/s 由式(11—11)得
專業資料
D
x0.023Re0.83
Sc0.44 ?
d
0.826x10-5㎡/s
15.53
0.44 3.05x10-2m
x0.023x(1.02x10+)0.83
)x
8.26 =1.746x10-2m/s
碘蒸氣在管壁上的沉積是對流傳質過程,故有
N=hm(cm-cw)=1.746x10-2m/sx(cm-0)
=1.746x10-2m/sxcm[單位為kmo1/(㎡2.s)]
討論:(1)本例中忽略了碘蒸氣的存在對空氣物性的影響,這只有在系統中碘蒸氣的濃度較低時適用。當碘蒸氣的質量濃度較高時,應按混合氣體的法則計算各物性。(2)注意到,對流傳質中hm的單位為m/s,這是速度的單位。由式(11—10b)可以看出,hm的大小代表了單位面積上由于質交換的結果組分A離開相界面的
速度。本章中所得到的值1.746x10—2m/s與主流速度5.18m/s相比差兩個數量級,因而是完全可以不計其影響的。
例題11—3 總壓力為1.013x105Pa的濕空氣,干球溫度為20℃,濕球溫度為10℃,試確定相對濕度。
題解
假設:含有水蒸氣的空氣按理想氣體處理,取水蒸氣在空氣中擴散時的Sc=0.60,空氣的P,=0.70。
計算:
a Sc 0.60
=0.857,(/)23
=0.902 D P. 0.70
按平均溫度15℃查空氣物性,得p=1.226kg/m3,cp=1.005kJ/(kg.K)。由水蒸氣性質表查得,與濕球溫度對應的飽和蒸汽壓p=1.227x103Pa。于是有。
專業資料
Pw
1.227x103Pa
0.0094kg/m3 Pw=
R,T 8314
㎡/(s2.K)x283K 18
水蒸氣在10℃時的汽化潛熱r=2247.7kJ/kg,由式(11—16)可得P2=Pn-c(/)23
20℃-10℃ =0.0094kg/m3
x1.226kg/m3x1.005kJ/(kg.K)x0.901 2477.7kJ/kg
=(0.0094-0.00448)kg/m3=0.00492kg/m3
據理想氣體狀態方程,來流中水蒸氣的分壓力為
p=pRT=0.00942kg/mx462m(K)x283K=6.43x102Pa 20℃時水蒸氣的飽和壓力p3=2.34x10Pa,故得相對濕度值為
0.643
x100%=27.5% 2.34
討論:按t是絕熱飽和溫度的假設可算得相對濕度為24.5%[6]:就濕度測定而言,這兩個結果間的差異是可以接受的。同時,考慮到傳熱、傳質計算中在Sc 數取值上的不確定性,因而實用上常采用熱力學的方法由干球溫度及濕球溫度來確定相對濕度[5,6,7]。
專業資料







