昨天與群員閑聊，偶然得知有計算模型體積的需要，這需求在游戲行業基本上用不到，一般在工業仿真或者3D打印等方面用得較多，據稱

昨天與群員閑聊，偶然得知有計算模型體積的需要，這需求在游戲行業基本上用不到，一般在工業仿真或者3D打印等方面用得較多，據稱某群員之前用蒙特卡洛模擬實現了，考慮到各平臺語法不太一樣，我剛好會一點unity3D引擎，因此復盤一個簡單的demo來講解一下該法的原理。

蒙特卡洛法，又稱隨機模擬法。它利用了統計學中的一個簡單的原理：當試驗次數足夠大，頻率就可以近似地等同于概率。該法的一個典型應用就是蒲豐投針試驗：

該試驗通過求解概率，可以用于計算圓周率，具體推導無需深究，其公式為：當平面上畫滿了間距為 ?a 的?平行直線，向該平面隨機拋擲一個長度為 l (l<a) 的針，則多次拋擲后，針與直線的相交概率為：

于是可以反推出π的近似數值。

回到模型體積的問題上，我們假設這樣一個場景：在空間中存有一個模型，模型的外部包有一個稍大的球殼，若我們隨機在球殼內生成一個點，那么該點要么在模型內，要么在模型外；由于球殼的體積是已知的，那么統計模型內的點的數量，計算它占總點數的比例，乘以球殼的體積，即為近似的模型體積。

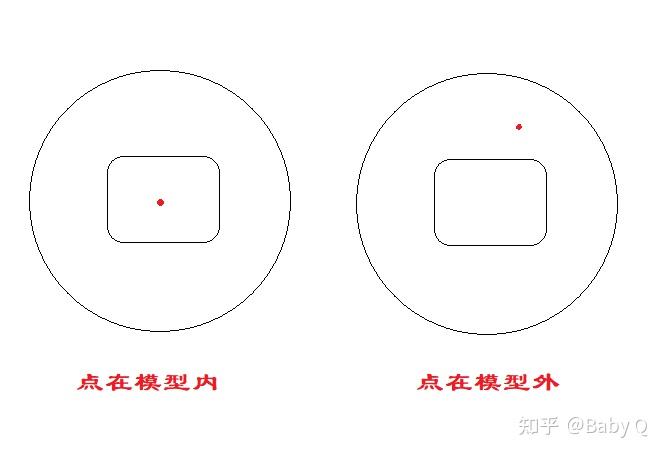
為便于進行測試，我使用6個plane搭建了一個長寬高均為10的立方體（為什么不用自帶的cube，這個我們稍后再說），便于后續分析偏差度。

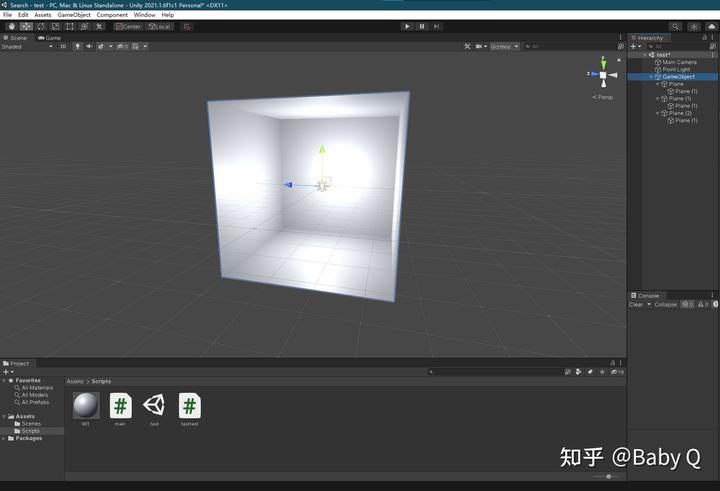
然后動態生成一個半徑為25的虛擬球殼，并生成五百萬個點進行模擬，以下是具體代碼：

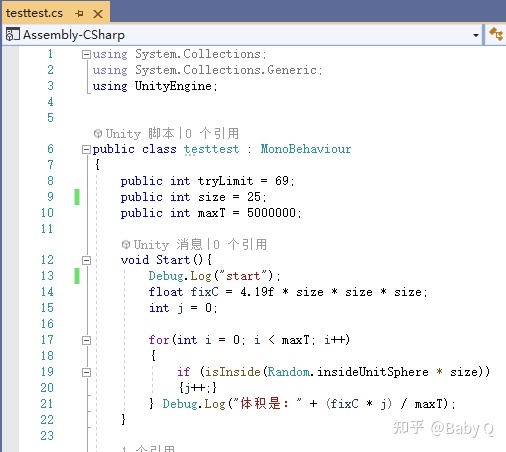
邏輯很簡單，for循環五百萬次，每次通過random函數生成一個隨機的坐標點，并乘以size系數來讓它遍布球殼內部，然后進行判定，若在模型內，則對變量 j 累加一次，最后除以總次數計算概率，乘以球殼體積即可，此處的 4.19 是 球形體積公式：V = ???πr3 前部的 ???π 的數值，便于作為固定系數簡化運算，以下是多次運行的幾次結果：

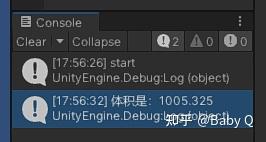
以第一次模擬為例，結果為“體積是1005”，我們搭建模型的標準體積是10*10*10=1000，存有千分之五的誤差，還是可以接受的。通過時間戳可以看到，從啟動到計算完成，共花費 32-26=6秒，如果減小模擬次數，可以進一步縮短計算時間，對誤差存有少量影響。

以上為蒙特卡洛法計算體積的主要原理，還存有很多需要完善的部分，如，對于每一次生成的隨機點，需要判斷它在模型的內部還是外部，unity中并沒有提供相關的API，因此我自行實現了一個方法，即上圖中的 isInside（）方法，以下為具體代碼：

該方法同樣采用了隨機的理念來進行判定，原理為：對于一個隨機的點，它向著任意方向發射多條射線，若該點存在于模型內，則所有的射線都會打在模型上，若該點在模型外，則至少有一條射線是不與模型碰撞的。

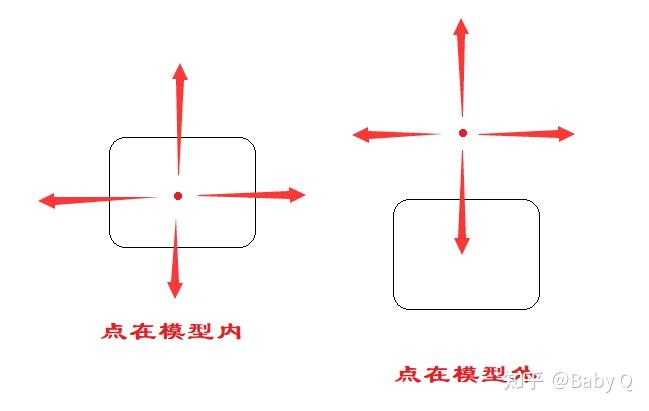
當然，這里涉及到一個問題，如果射線連續多次都打在了模型上，誰能知道下一條射線會不會就沒有打到模型呢？這里用概率論簡要地解釋一下：

對于一個在模型外的點，在它的各個方向中，面對模型的方向，其”視角“通常遠小于背向模型的方向。假設打不中的概率是0.6，打中的概率是0.4，對于一個在模型外的點，隨機的十次射線都打中模型的概率只有0.4的十次方，即萬分之一。

因此，我設定了一個射線次數上限 tryLimit，數值為69，即在69次的隨機試驗中，如果存有一次射線未打中模型的情況，則返回 false（表明該隨機點在模型外），若69次都打中模型了，則返回 true（表明該隨機點在模型內）。 over

PS: 經過實際debug測試，tryLimit在39左右即可保存相當的判定精度，但如果你要處理的模型存有很多溝/槽等結構，建議上調 tryLimit到99。

PPS：如果你已經看懂了，就會意識到射線是本方法的核心，但由于unity引擎的預置模型都為單面渲染，導致射線會從內部穿過，因此本文的開頭才臨時采用plane來進行測試，如果你需要對導入的模型進行處理，就需要將其轉為雙面顯示，讀者自行網絡學習 shader 相關知識即可。

PPPS：“虛擬球殼”并非必要的手段，如果難以確定導入模型的大致空間范圍，可以采用計算AABB包圍盒來作為模擬空間，然后利用random.range函數產生三個坐標值，以生成模擬空間內的坐標點，然后進行蒙特卡洛模擬即可。