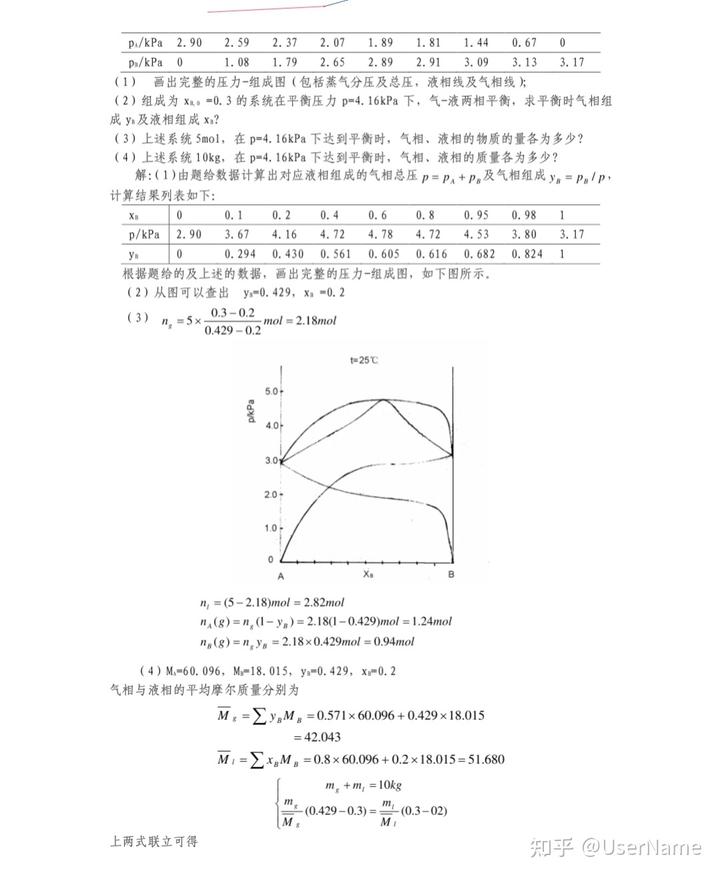
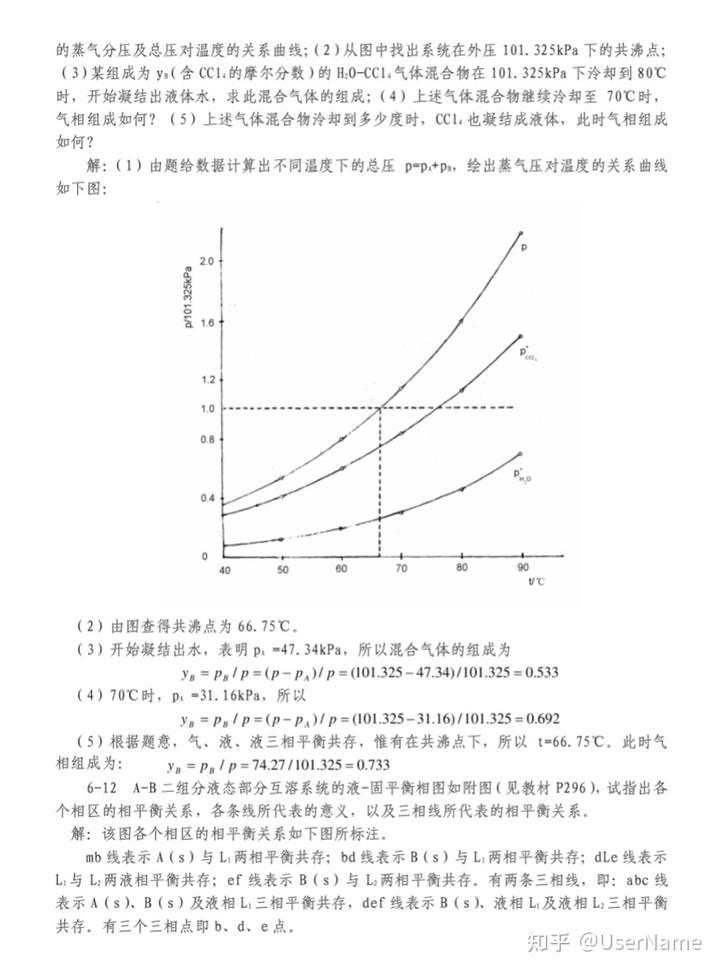
69.9-33.3 m(L1)=300xg=179.6g, m(L2)=300g-179.6g=120.4g 69.9-8.75 (2)苯酚=200/(200+200)=50
解答:現象請看左圖動畫。即小液滴逐漸變小,最后消失;大液滴逐漸變大。原因在于大液滴飽和蒸氣壓更小罩內的蒸氣壓先達到大液滴的飽和
解答:現象請看左圖動畫。即小液滴逐漸變小,最后消失;大液滴逐漸變大。
原因在于大液滴飽和蒸氣壓更小罩內的蒸氣壓先達到大液滴的飽和蒸氣壓,從而不斷凝結在大液滴上,而小液滴不斷蒸發,最終消失。二維晶核長大機制(
(Two-dimensional
nucleation)②
光滑界面每向液相中長大一層O
①
都是由一個二維晶核(一個原o
0
子厚度的晶體小片)先在界面
上形成,接著這個二維晶核側
向生長,如此反復進行,直至4
結晶完成。由于形成二維晶核
需要形核功,這種機制的晶體
長大速率很慢Figure 4: Crystal growth by two-dimensional mechanism
6
6/212.5晶核的長大
螺型位錯長大機制(Screw dislocation
mechanism)
液相原子可以直接添加到界
面上由于晶體缺陷而形成的
臺階上,從而使晶體不斷長
大。如螺型位錯在界面露頭
就可以提供臺階。由于界面
上臺階數量有限,這種機制
下晶體生長速率也很小Figure 3: Crystal growth by screw dislocations
7/212.5晶核的長大
連續或垂直長大機制 (Vertical growth)粗
相似文檔
約有50%的結晶位置空著,液相原子可以直接進入這些位置,在線打開下載到網盤
收藏分享
發送PC302人工晶體學報
第36卷
(THM)、區熔法等。為改進晶體的生長質量,這些生長方法還采用了施加磁場、高壓、加速堝旋轉(accelerated crucible rotation technique,簡稱 ACRT)、蒸汽壓控制.、微重力等技術來優化溫度場和熔體對流場。
位錯是熔體定向凝固法生長單晶體過程中不可避免的缺陷之一,特別是對于化合物半導體,由于晶體的生長溫度高、熱導率低,臨界切應力較小,在熱應力的作用下晶體更容易發生塑性變形,產生高密度位錯。熔體法生長晶體過程中,位錯產生的原因是:(1)軸向溫度梯度和徑向溫度梯度引起的熱應力;(2)對于晶體-坩堝接觸的生長系統,晶體與坩堝的熱膨脹系數不同,也會造成熱應力的產生;(3)空位、雜質偏析、沉淀相等缺陷引起晶格不匹配,從而造成局部應力集中。熱應力是位錯產生的主要因素,在應力的作用下,位錯會發生運動和增殖。
本文擬闡述現有的半導體單晶位錯模型,分析晶體生長過程中影響位錯產生、增殖的各種因素,以及抑制位錯增殖的措施。
2單晶位錯研究模型
對半導體單晶位錯的產生與增殖研究,其數學物理模型主要有基于熱彈性理論的臨界切應力模型,即CRSS( Critical Resolved Shear Stress)模型和考慮晶體高溫塑性變形的粘塑性模型( Visco-plasticityModel) [3.19-26]
2.1臨界切應力(CRSS)模型
假設晶體為各向同性的線彈性體,柱坐標系下,不計體力項時晶體內點元的力平衡方程為:
0+7+0.-0=0
ar az 1(1)

































































































































































































































































































00+T
=
0
zar
(2)
幾何關系為:du
u
du
=,E
=,6:
,Ym
=+
aw
ardz
dz
(3)
應力-應變關系由Hooke定律得到:Cu
C2C120B,-a1T-Tmi
C12CHC06-aT-TM
=(4)
0C12
C12C0-a|T-TM
00
0 Cu
Y
臨界切應力即為由實驗測得的材料的臨界屈服應力,臨界切應力模型認為在凝固時產生的熱應力大于晶體的臨界切應力,即5
CRSS >0
(5)
第一章氣體的pVT關系
1-1物質的體膨脹系數a與等溫壓縮系數K的定義如下:
a=()x,--()
試導出理想氣體的a1、K與壓力、溫度的關系?
解:對于理想氣體,pV=nRT
a())=
x(),(),-
1-2氣柜內有121.6kPa、27℃的氯乙烯(C:HC1)氣體300m,若以每小時90kg的流量
輸往使用車間,試問貯存的氣體能用多少小時?
解:設氯乙烯為理想氣體,氣柜內氯乙烯的物質的量為
pV121.6×103×300=14618.623mol
RT8.314×300.15
每小時90kg的流量折合p摩爾數為y90×10390×103=1441.153mol-h
McH,CI62.45
n/v=(14618.623÷1441.153)=10.144小時
1-30℃、101.325kPa的條件常稱為氣體的標準狀況。試求甲烷在標準狀況下的密度。解:PCH=MCH=M CH=101325×16×10
=0.714kg-m
8.314×273.15
1-4一抽成真空的球形容器,質量為25.0000g。充以4℃水之后,總質量為125.0000g。
若改用充以25℃、13.33kPa的某碳氫化合物氣體,則總質量為25.0163g。試估算該氣體的
摩爾質量
解:先求容器的容積V=125.0000-25.000100.0000cm3=100.0000cm
PH-0()
n=m/M-pV/RT
M=-
RTm8.314×298.15×(25.0163-25.0000)=30.31gmol
pV13330×10
1-5兩個體積均為V的玻璃球泡之間用細管連接,泡內密封著標準狀況條件下的空氣。
若將其中一個球加熱到100℃,另一個球則維持0℃,忽略連接管中氣體體積,試求該容器
內空氣的壓力。
解:方法一:在題目所給出的條件下,氣體的量不變。并且設玻璃泡的體積不隨溫度而
變化,則始態為n=n1+n2=2pV(RT)
終態(f)時n=n
1.2.()()
”()()
2×101.325×373.15×273.15=117.00kPa
273.15(373.15+273.15)
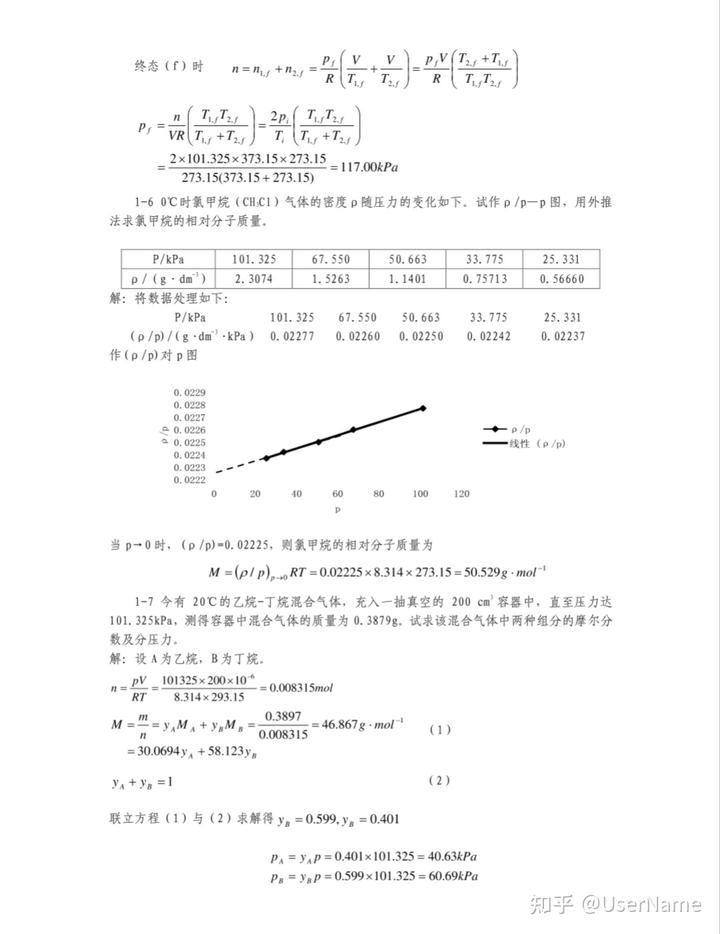
1-60C時氯甲烷(CHC1)氣體的密度p隨壓力的變化如下。試作p/p一p圖,用外推法求氯甲烷的相對分子質量。
P/kPa101.325
67.550
50.663
33.775
25.331
p/(g·dm3)2.3074
1.5263
1.1401
0.75713
0.56660
解:將數據處理如下:
P/kPa101.325
67.55050.66333.775
25.331
(p/p)/(g-dmkPa)0.022770.022600.022500.022420.02237
作(p/p)對p圖
0.0229
0.0228
0.0227
0.0226p/p
0.0225線性(p/p)
0.0224
0.0223
0.0222020
40
60
80
100
120
當p→0時,(p/p)=0.02225,則氯甲烷的相對分子質量為
M=(p/p)RT=0.02225×8.314×273.15=50.529g . mol
1-7今有20℃的乙烷-丁烷混合氣體,充入一抽真空的200cm容器中,直至壓力達101.325kPa,測得容器中混合氣體的質量為0.3879g。試求該混合氣體中兩種組分的摩爾分數及分壓力。
解:設A為乙烷,B為丁烷
pV101325×200×10=0.008315mol
RT8.314×293.15
M=m=yAMA+yBMB=0.3897=46.867g-mol
0.008315(1)
=30.0694y+58.123y
yA+yB=1(2)
聯立方程(1)與(2)求解得y=0.599.y=0.401
PA=yAP=0.401×101.325=40.63kPa
PB=yBP=0.599×101.325=60.69kPa
1-8如圖所示一帶隔板的容器中,兩側分別有同溫同壓的氫氣與氮氣,二者均克視為理想氣體。H
3dm
N:
1dm'
Tp
T
(1)保持容器內溫度恒定時抽去隔板,且隔板本身的體積可忽略不計,試求兩種氣體混合后的壓力。
(2)隔板抽去前后,H:及N:的摩爾體積是否相同?
(3)隔板抽去后,混合氣體中H:及N:的分壓力之比以及它們的分體積各為若干?
解:(1)抽隔板前兩側壓力均為p,溫度均為T
PPP(1)
得:n2=3nN
而抽去隔板后,體積為4dm,溫度為,所以壓力為
p-=,+,(2)
Idm
比較式(1)、(2),可見抽去隔板后兩種氣體混合后的壓力仍為p
(2)抽隔板前,H的摩爾體積為V_n=RT/p,N2的摩爾體積VN=RT/P
抽去隔板后V=nH2Vm.2+nN2Vm.N2=nRT/p=(3nN2 +nN2 )RT/ p
3n RT n RT
PP
DH2=3nN2
所以有H =RT/p, VN =RT/P
可見,隔板抽去前后,H:及N:的摩爾體積相同。
(3)yHSnNS
=1
+3n3o.I
Pw,=Ym,P-=P:PM,-=YM,P=GP
3
所以有Pu:P,-3:1
Vn1=yn1V=x4=3dm
VN2=yx2V=x4=1dm
1-9氯乙烯、氯化氫及乙烯構成的混合氣體中,各組分的摩爾分數分別為0.89、0.09和0.02。于恒定壓力101.325kPa條件下,用水吸收掉其中的氯化氫,所得混合氣體中增加了分壓力為2.670kPa的水蒸氣。試求洗滌后的混合氣體中CHC1及CH的分壓力。
解:洗滌后的總壓為101.325kPa,所以有
Pc2H3C1+Pc2H1=101.325-2.670=98.655kPa(1)
PCHCPCH =yCHclycH =ncHcncH =0.89/0.02(2)
聯立式(1)與式(2)求解得
PCHC=96.49kPa; PCH =2.168kPa
1-10室溫下一高壓內有常壓的空氣。為進行實驗時確保安全,采用同樣溫度的純氮進行置換,步驟如下向釜內通氮直到4倍于空氣的壓力,爾后將釜內混合氣體排出直至恢復常壓。這種步驟共重復三次。求釜內最后排氣至年恢復常壓時其中氣體含氧的摩爾分數。設空氣中氧、氮摩爾分數之比為1:4.
解:高壓釜內有常壓的空氣的壓力為p,氧的分壓為
Po2=0.2P常
每次通氮直到4倍于空氣的壓力,即總壓為
p=4ps,
第一次置換后釜內氧氣的摩爾分數及分壓為
y===2
=0.05
P2.=P常×y02=0.05×P常
第二次置換后釜內氧氣的摩爾分數及分壓為0.05p常0.05
yo:2D4p常
4
0.05
PO2.2=P常×yO2.2=〤P常
所以第三次置換后釜內氧氣的摩爾分數
Po,2(0.05/4)P常0.05
yo23=0.00313=0.313%
4p常16
1-1125℃時飽和了水蒸汽的乙炔氣體(即該混合氣體中水蒸汽分壓力為同溫度下水的飽和蒸氣壓)總壓力為138.7kPa,于恒定總壓下冷卻到10℃,使部分水蒸氣凝結成水。試求每摩爾干乙炔氣在該冷卻過程中凝結出水的物質的量。已知25℃及10℃時水的飽和蒸氣壓分別為3.17kPa和1.23kPa.
解:PB=yBP,故有
PBIPA=yByA=nBInA=PB(P-PB)
所以,每摩爾干乙炔氣含有水蒸氣的物質的量為
進口處:3.17
=0.02339(mol)
138.7-3.17
出口處:123
=0.008947(mol)
138.7-123
每摩爾干乙炔氣在該泠卻過程中凝結出的水的物質的量為
0.02339-0.008974=0.01444(mol)
1-12有某溫度下的2dm3濕空氣,其壓力為101.325kPa,相對濕度為60%。設空氣中O2和N2的體積分數分別為0.21和0.79,求水蒸氣、O2和N2的分體積。已知該溫度下水的飽和蒸氣壓為20.55kPa(相對濕度即該溫度下水蒸氣分壓與水的飽和蒸氣壓之比)
解:水蒸氣分壓=水的飽和蒸氣壓×0.60=20.55kPa×0.60=12.33kPa
O2分壓=(101.325-12.33)×0.21=18.69kPa
N2分壓=(101.325-12.33)×0.79=70.31kPa
Vo2=yo2Po:18.69
×2=0.3688dm
101.325
PN70.31
×2=1.3878dm3
101.325
V=yoV=P=12.33×2=0.2434dm
101.325
1-13一密閉剛性容器中充滿了空氣,并有少量的水,當容器于300K條件下達到平衡時,器內壓力為101.325kPa。若把該容器移至373.15K的沸水中,試求容器中達到新的平衡時應有的壓力。設容器中始終有水存在,且可忽略水的體積變化。300K時水的飽和蒸氣壓為3.567kPa.
解:300K時容器中空氣的分壓為p=101.325kPa-3.567kPa=97.758kPa
373.15K時容器中空氣的分壓為
373.15373.15
p空=P空
×97.758=121.534(kPa)
300300
373.15K時容器中水的分壓為PH0=101.325kPa
所以373.15K時容器內的總壓為
p= P+Po=121.534+101.325=222.859 (kPa)
1-14CO氣體在40℃時的摩爾體積為0.381dm3·mol設CO2為范德華氣體,試求其壓力,并與實驗值5066.3kPa作比較。
解:查表附錄七得CO2氣體的范德華常數為
a=0.3640Pa· m mol2; b=0.4267× 10m3 mol
RT a8.314×313.15
0.3640
p=(V-b)V20.381×10-3-0.4267×10-4(0.381×10-3)2
2603.5291-2507561=7695236-2507561=5187675Pa
0.33833×10
=5187.7kPa
相對誤差E=5187.7-5066.3/5066.3=2.4%
1-15今有0℃、40530kPa的氮氣體,分別用理想氣體狀態方程及范德華方程計算其摩
爾體積。其實驗值為70.3cm3·mol
解:用理想氣體狀態方程計算如下:
V=RT/p=8.314×273.15÷40530000
=0.000056031m3. mol=56.031cm3-mol
將范德華方程整理成V-(b+RT/p)V2+(al pv-ablp=0 (a)查附錄七,得a=1.408×10'Pa·m6·mol2,b=0.3913×10m3·mol這些數據代入式(a),可整理得
{V2/(m3-mol-1)}-0.9516×10-+{Vm/(m3·mol-1)}2
+3.0×10(V/(m3.mol)}-1.0×103=0解此三次方程得Vm=73.1 cm3. mol
1-16函數1/(1-x)在-1<x<1區間內可用下述冪級數表示:
1/(1-x)=1+x+x2+x3+.
先將范德華方程整理成n=()
再用述冪級數展開式來求證范德華氣體的第二、第三維里系數分別為
B(T)=b-a(RT)C=(T)=b2
解:1/(1-b/Vm)=1+b/Vm+(b/Vm)2+.
將上式取前三項代入范德華方程得
p=
(1a RT RTh-a RTh?
vvvv
而維里方程(1.4.4)也可以整理成
RT RTB RTC
p=VV2V
0
根據左邊壓力相等,右邊對應項也相等,得
B(T)=b-a/(RT)C(T)=b2
*1-17試由波義爾溫度TB的定義式,試證范德華氣體的TB可表示為
TB=a/(bR)
式中a、b為范德華常數。
解:先范德方程整理p=nTan
(V-nb)V2
將上式兩邊同乘以V得pV-nRTy an
(V-nb)V
求導數
()(V-nb)nRT-nRTVan2anbn2RT
(V-nb)?V2
V2(V-nb)?
當p→0時[(pV)1p],=0,于是有an2_bn2RT
=0
y2(V-nb)2
T
(V-nb)7a
brva
當p→0時V→∞,(V-nb)2≈V2,所以有TB=a/(bR)
1-18把25℃的氧氣充入40dm3的氧氣鋼瓶中,壓力達202.7×10kPa。試用普化壓
縮因子圖求解鋼瓶中氧氣的質量
解:氧氣的臨界參數為Tc=154.58K
Pc=5043kPa
氧氣的相對溫度和相對壓力T=T/Tc=298.15/154.58=1.929
p1=p/pc=202.7×102/5043=4.019
由壓縮因子圖查出:Z=0.95
_pV_202.7×102×40×10-3
-mol=344.3mol
ZRT0.95×8.314×298.15
鋼瓶中氧氣的質量mo =nMo =344.3×31.999×103kg=11.02kg
1-19
1-20
1-21在300k時40dm3鋼瓶中貯存乙烯的壓力為146.9×10kPa.欲從中提用300K
101.325kPa的乙烯氣體12m3,試用壓縮因子圖求解鋼瓶中剩余乙烯氣體的壓力
解:乙烯的臨界參數為Tc=282.34K
Pc=5039kPa
乙烯的相對溫度和相對壓力T,=T/Tc=300.15/282.34=1.063
p,=p/pc=146.9×102/54039=2.915
由壓縮因子圖查出:Z=0.45
pV146.9×102×103×40×103
-mol=523.3(mol)
ZRT0.45×8.314×300.15
因為提出后的氣體為低壓,所提用氣體的物質的量,可按理想氣體狀態方程計算如下:pV101325×12
提RT8.314×300.15mol=487.2mol
剩余氣體的物質的量
n=n-n=523.3mol-487.2mol=36.1mol
剩余氣體的壓力p1=Z1n1RT36.1×8.314×300.15Z1
Pa=2252ZkPa
40×10
剩余氣體的對比壓力p=p1/pc=2252Z1/5039=0.44Z
上式說明剩余氣體的對比壓力與壓縮因子成直線關系。另一方面,T=1.063。要同時滿
足這兩個條件,只有在壓縮因子圖上作出p=0.44Z,的直線,并使該直線與T=1.063的等
溫線相交,此交點相當于剩余氣體的對比狀態。此交點處的壓縮因子為
Z=0.88
所以,剩余氣體的壓力
p1=2252Z1kPa=2252×0.88kPa=1986kPa
第二章熱力學第一定律
2-11mol理想氣體于恒定壓力下升溫1C,試求過程中氣體與環境交換的功W.
解: W =-Pm(V2 -V1)=-pV2 + pV1 =-nRT2 + nRT1 =-nR△T =-8.314J2-21mol水蒸氣(H2O,g)在100℃,101.325kPa下全部凝結成液態水。求過程的功。
: W =-Pmb(V1 -Vg) PmV = p(nRT/p)=RT=8.3145×373.15=3.102kJ
2-3在25C及恒定壓力下,電解1mo1水(H0,1),求過程的體積功
H2O(1)=H2(g)+O2(g)
解:1mo1水(H:0,1)完全電解為1molH:(g)和0.50mo10:(g),即氣體混合物的
總的物質的量為1.50mo1,則有
W=-Pamb(Vg-VH20()=-PambVg =-p(nRT/p)
=-nRT=-1.50×8.3145×298.15=-3.718kJ2-4系統由相同的始態經過不同途徑達到相同的末態。若途徑a的Q.=2.078kJ,W=
-4.157kJ;而途徑b的Q=-0.692kJ。求W
解:因兩條途徑的始末態相同,故有△U=△U,則Q+W=Q+W所以有,W=Q+W-Q=2.078-4.157+0.692=-1.387kJ
2-5始態為25℃,200kPa的5mol某理想氣體,經a,b兩不同途徑到達相同的末態
途徑a先經絕熱膨脹到-28.57℃,100kPa,步驟的功W=-5.57kJ;在恒容加熱到壓力200
kPa的末態,步驟的熱Q=25.42kJ。途徑b為恒壓加熱過程。求途徑b的W及Qb
解:過程為:5mol5mol
5mol
25CW=-5.57kJ,Q
=028.57C
=25.42k/.W=0
200kPa100kPa
200kPa
V2V2
途徑b
V=nRT/p1=5×8.3145×298.15+(200×103)=0.062m
V2=nRT2p2=5×8.3145×(-28.57+273.15)÷(100×103)=0.102m3
W=-p(V2-V1)=-200×103×(0.102-0.062)=-8000J=-8.0kJ
W=W+W"=-5.57+0=-5.57kJ
Q=Q+Q=0+25.42=25.42kJ
因兩條途徑的始末態相同,故有△U=△U,則Q+W=Q+W
Q=Q+W-W=25.42-5.57+8.0=27.85kJ
2-64mol某理想氣體,溫度升高20℃,求△H-△U的值
解:
△H-△U=nC,dT-nCdT
-fn(Cm-C.==nR(T+20K-T)
=4×8.314×20=665.16J
2-7已知水在25℃的密度p=997.04kg·m3求1mol水(H:0,1)在25C下:(1)壓力從100kPa增加到200kPa時的△H
(2)壓力從100kPa增加到1MPa時的△H.
假設水的密度不隨壓力改變,在此壓力范圍內水的摩爾熱力學能近似認為與壓力無關解:△H=△U+△(pV)
因假設水的密度不隨壓力改變,即V恒定,又因在此壓力范圍內水的摩爾熱力學能近似
認為與壓力無關,故△U=0,上式變成為
△H=V△P=V(P2-P1)=M(P2-P1)
(1)△H=Mn1o(P2-P1)=18×10×(200-100)×103=1.8J
997.04
(2)△H=M(p2-p1)=18×10×(1000-100)×103=16.2J
997.04
2-8某理氣體C=1.5R。今有該氣體5 mol在恒容下溫度升高50℃,求過程的W,Q,
△H和△U
解:恒容:W=0;
△U=[nCdT=nCvm(T+50K-T)
=nCvx50K=5x÷×8.3145×50=3118J=3.118kJ
AH=nC_dT=nC_(T+50K-T)=n(Cv+R)×50K
=5××8.3145×50=5196J=5.196kJ
根據熱力學第一定律,:W-0,故有Q-△U=3.118kJ
2-9某理想氣體C=2.5R。今有該氣體5mol在恒壓下溫度降低50℃,求過程的W,
Q,△H和△U.
解:
△U=nCvdT=nCvm(T-50K-T)
=nC×(-50K)=-5x×8.3145×50=-5196J=-5.196kJ
△H=nCndT=nCnm(T-50K-T)
=nCnm×(-50K)=-5××8.3145×50=-7275J=-7.275kJ
Q=△H=-7.275kJ
W=△U-Q=-5.196kJ-(-7.725kJ)=2.079kJ
2-10 2mo1 某理體, Crm=R態100 kPa, 50 dm3,先恒容加熱使壓力升
高至200kPa,再恒壓泠卻使體積縮小至25dm。求整個過程的W,Q,△H和△U.
解:整個過程示意如下:2mol2mol
2mol
W=0T2
>
T3
100kPa200kPa
200kPa
50dm50dm3
25dm3
T=
PV100×103×50×103=300.70K
nR2×8.3145
T=P2V2
200×103×50×10=601.4K
nR2×8.3145
TP3V3200×103×25×10=300.70K
nR2×8.3145
W2=-p2×(V3-V1)=-200×103×(25-50)×103=5000J=5.00kJ
W=0: W2=5.00kJ: W=W+W2 =5.00kJ
: T=T=300.70K;. AU=0, AH=0
AU=0. Q=-W=-5.00kJ
2-11 4 mol 某理想體, C=R.態100 kPa, 100 dm',先恒壓加熱使體增
大到150dm3,再恒容加熱使壓力增大到150kPa。求過程的W,Q,△H和△U.
解:過程為4mol
4mol
4mol
Tw
T2
W=0
T3
100kPa100kPa
150kPa
100dm150dm
150dm
T=
PV100×103×100×103=300.70KT2
P2V:100×103×150×10=451.02K
nR4×8.3145
nR
4×8.3145
7=P.V.I
150×10×150×10=676.53K
nR4×8.3145
W1=-p,×(V3-V1)=-100×103×(150-100)x103=-5000J=-5.00kJW2=0;W=-5.00kJ; W=W+W=-5.00k
△U=[or.[n(Cnm-R)dT=nxRx(T3-T1)
=4××8.314×(676.53-300.70)=18749J=18.75kJ
AH=[nC,dT=nxRx(T,-T,)=4xx8.314x(676.53-300.70)=31248J=31.25JQ=△U-W=18.75kJ-(-5.00kJ)=23.75kJ
2-12已知CO2(g)的
Cp m =26.75+42.258 × 103(T/K)-14.25 × 106(T/K) 2) J mol K
求:(1)300K至800K間CO2(g)的Cm
(2)1kg常壓下的CO2(g)從300K恒壓加熱至800K的Q
解:(1):
△Hm=[CdT
=(26.75+42.258x10-3(T/K)-14.25x106(T/K)2)d(T/K)J-mol
=22.7kJ-mol
Cp.m =AH/AT =(22.7×103)/500J.mol. K=45.4J .mol-1. K-
(2):△H=n△Hm=(1×103)÷44.01×22.7kJ=516kJ
2-13已知20C液態乙醇(CH0H,1)的體膨脹數a=1.12×10-3K-1,等
溫壓縮系數,=1.11×10Pa-1,密度p=0.7893g·cm3,摩爾定壓熱容
Cp=114.30J-molK求20℃,液態乙醇的Cm
解:1mol乙醇的質量M為46.0684g,則
V=Mp
=46.0684g·mol'÷(0.7893 g·cm3)=58.37cm3mo1'=58. 37× 10'm3 mo1
由公式(2.4.14)可得:
Cm=Cm-TVmaKT
=114.30J.mol.K-293.15K×58.37×10m3.molx(1.12×103K)2÷1.11x103Pa=114.30J.mol.K-19.337J.mol.K=94.963J.mol.K
2-14容積為27m3的絕熱容器中有一小加熱器件,器壁上有一小孔與100kPa的大氣相
通,以維持容器內空氣的壓力恒定。今利用加熱器件使容器內的空氣由0℃加熱至20℃,問
需供給容器內的空氣多少熱量。已知空氣的C=20.4J-mol.K
假設空氣為理想氣體,加熱過程中容器內空氣的溫度均勻。
解:假設空氣為理想氣體n
pV
RT
Q=Q,=ΔH=nC,T=C,YaT
=C'dnT =(C+R)
=(20.40+8.314)x100000x27293.15=6589J=6.59k/
8.314
2-15 容積為0.1m3的恒容密閉容器中有一絕熱隔板,其兩側分別為0℃, 4mol 的Ar
(g) 及 150℃,2mol 的 Cu(s).現將隔板撤掉,整個系統達到熱平衡,求末態溫度 t 及過
程的△H.
已知: Ar (g)和Cu (s)的摩爾定壓熱容C,..分別為20.786 J-mol-'-K-'及
24.435 J-mol-1-K-',且假設均不隨溫度而變。
解:用符號 A代表 Ar(g),B代表Cu(s);因 Cu是固體物質,CC,;而
Ar (g): Cy=(20.786-8.314)J·mol-1·K-1=12.472J-mol-'.K-1
過程恒容、絕熱,W=0, Q=△U=0.顯然有
△U = △U(A)+△U(B)
=n(A)Cvm(A)(T,-T(A)}+n(B)Cv.m(B)(T,-T,(B)}=0
得T2 =
n(A)Cv(A)T, (A)+n(B)C(B)T,(B)
n(A)Cv(A) + n(B)Cy (B)
4×12.472×273.15+2×24.435×423.15
K = 347.38K
所以,t=347.38-273.15=74.23℃
4×12.472+2×24.435
ΔΗ = ΔΗ(A)+ΔΗ(B)
=n(A)CAm (A)(T2-7,(A)}+n(B)C(B)(T2-7,(B))
ΔΗ = 4×20.786×(347.38-273.15)J+2×24.435×(347.38-423.15)J
=6172J-3703J=2469J=2.47kJ
2-16 水煤氣發生爐出口的水煤氣溫度是 1100℃,其中 CO(g)及 H2(g)的體積分數
各為 0.50.若每小時有 300kg水煤氣有 1100℃ 泠卻到 100℃,并用所回收的熱來加熱水,使
水溫有 25℃升高到 75℃.試求每小時生產熱水的質量。
CO(g) 和 H2(g)的摩爾定壓熱容 Cp,m 與溫度的函數關系查本書附錄,水(H2O,
1)的比定壓熱容cp=4.184 J.g-.K-1。
解:已知 Mн,=2.016, Mco=28.01, Ун,=yco=0.5
水煤氣的平均摩爾質量
M=yн,Мн, +ycoMco=0.5x(2.016+28.01)=15.013
300kg水煤氣的物質的量300×10
n=-mol = 19983mol
15.013
由附錄八查得: 273K-3800K的溫度范圍內
Cp(H2)= 26.88J·mol-.K-+4.347×10-J-mol--K-2T-0.3265×10J-mol-.K-3T2Cp(CO)= 26.537J-mol--K-1+7.6831×10-J-mol--K-2T-1.172×10°J-mol--K-3T2
設水煤氣是理想氣體混合物,其摩爾熱容為
Cp.m(mix)ΣyC,(B)=0.5x(26.88+26.537)J-mol-.κ-1
+0.5×(4.347+7.6831)×10-3J·mol-1-K-T
-0.5×(0.3265+1.172)×10°J-mol-K-T
故有
Cp.m(mir)=26.7085J-mol-1·K-1+6.01505×10-J-mol--K-T
-0.74925×10°J-mol.K-T2
73.15K
得Q,=ΔΗ=
J373.5K Cp.mmir)dT
2, = 1 (26.7085J -mol"-?
+6.0151×10-J·mol--K-T-0.74925×10°J-mol·K-T2aT
26.7085× (373.15-1373.15) J-mol-
+1×6.0151× (373.152-1373.152) ×10'J·mol-
2
-1 x 0.74925× (373. 15'-1373.15') x10*J-mol-
=-26708.5 J·mol-'-5252.08 J·mol-1+633. 66 J·mol-
=31327J-mol-1=31. 327 kJ-mol-1
19983 × 31.327=626007kJ
-Q, 626007×10°
m=-kg =2992387g = 2992.387kg = 2.99 x10kg
CpAr*·Δt 4.184× (75-25)
2-17 單原子理想氣體 A 與雙原子理想氣體 B 的混合物共 5mo1,摩爾分數 y,=0.4,始態溫度 T:=400 K,壓力 p:=200 kPa.今該混合氣體絕熱反抗恒外壓 p=100 kPa 膨脹到平衡態。求末態溫度 T:及過程的 W, △U,△H.
解:先求雙原子理想氣體 B 的物質的量: n (B) =yn×n=0.4×5 mol=2mol;則
單原子理想氣體 A的物質的量:n(A) =(5-2) mol =3mol
單原子理想氣體A的Cy-=R,雙原子理想氣體B的Cya=5
過程絕熱,Q=0,則AU=
n(A)Cvm (A)(T2-T,)+n(B)C(B)(T2-T,)=-Pamb (V2-V,)
3xR,-T+2RT,-T)--TT)
4.5x(T2-T,)+5x(T2-T,)=-nT, +nx(p /p,)T,=-57, +5x0.57
于是有
得14.5T,=12T=12 × 400K
T2=331.03K
V2=nRT, / p2= nRT,/Pam=5x8.314x331.03+100000m=0.13761m-3V,=nRT, /p,=5×8.314×400+200000m-=0.08314m"
AU =W=-Panb (V-V)=-100x103 ×(0.13761-0.08314)J=-5.447kJΔΗ = ΔU +Δ(pV)= ΔU +(p2V2-pV)
=-5447J +(100×103 ×0.13761-200 ×103 ×0.08314)J
=-5447.J-2867.J=-83141=-8.314kJ
2-18 在一帶活塞的絕熱容器中有一絕熱隔板,隔板的兩側分別為 2mo1,0℃的單原子
理想氣體 A 及 5mol,100℃的雙原子理想氣體 B,兩氣體的壓力均為 100 kPa. 活塞外的
壓力維持 100kPa 不變。
今將容器內的絕熱隔板撤去,使兩種氣體混合達到平衡態。求末態溫度T及過程的W
ΔU.
解:單原子理想氣體A的C=R,雙原子理想氣體B的C=2R
因活塞外的壓力維持100kPa不變,過程絕熱恒壓, Q-Q,-AH=0,于是有n(A)Cp(A)(T-273.15K)+n(B)C,(B)(T-373.15K)=0
2xR(T-273.15K)+5xR(T-373.15K)-0
5x(T-273.15K)+17.5x(T-373.15K)=0
于是有 22.5T=7895.875K得
ΔU =n(A)Cv.m(A)(T-273.15K)+n(B)Cy (B)(T-373.15K)
=2x 3×8.3145 x(350.93-273.15)J+5x5×8.3145×(350.93-373.15)J
T=350.93K
= 1940.1J-2309.4 = -369.3J = W
2-19 在一帶活塞的絕熱容器中有一固定絕熱隔板,隔板活塞一側為 2mol, 0℃的單原
子理想氣體 A,壓力與恒定的環境壓力相等;隔板的另一側為 6mol,100℃的雙原子理想氣
體 B,其體積恒定。
今將絕熱隔板的絕熱層去掉使之變成導熱隔板,求系統達平衡時的T 及過程的 W,△U.
解:過程絕熱,Q-0, △U-W,又因導熱隔板是固定的,雙原子理想氣體 B體積始終恒定,
所以雙原子理想氣體 B 不作膨脹功,僅將熱量傳給單原子理想氣體 A,使 A 氣體得熱膨脹作
體積功,因此,W=W.,故有AU=W=W
得
n(A)Cy(A)(T-273.15K)+n(B)C(B)(T-373.15K)=-Pamb (V2-V)2xR(T-273.15K)+6xR(T-373.15K)
=-pamb ((2RT / Pamb)-(2R×273.15K/ Pamb
3×(T-273.15K)+15×(T-373.15K)=-2T+2×273.15K
得20× T=6963K
故T=348.15K
V2.=nRT2/Pam=2x8.3145x348.15+100000m=0.05789m-3
V.A=nRT,/Pabm=2×8.3145×273.15+100000m-3=0.04542m-3
△U=W=-pamb (V2A-VA)=-100×103×(0.05789-0.04542)J=-1247J
2-20 已知水(H0,1)在 100℃ 的飽和蒸氣壓 p'=101.325 kPa,在此溫度、壓力下水
的摩爾蒸發焓AH=40.668kJ-mol-.求在 100℃, 101.325 kPa下使1kg 水蒸氣全部凝
結成液體水時的 Q,W,△U及 △H.設水蒸氣適用理想氣體狀態方程。
解:過程為 lkgH,O(g),100°C,101.325kPa→IkgH,O(1),100°C,101.325kPan=1000/18.01=55.524mol
Q=Q,= π×(-ΔpΗ?)=55.524×(-40.668)kJ =-2258kJ = ΔΗ
1000
W=-pamb (V,-V,)=pV,=n,RT=(-×8.314×373.15)J =172.35kJ
18
△U=Q+W=(-2258+172.35)=-2085.65kJ
2-17 今有溫度分別為 80℃、40℃ 及 10℃的三種不同的固體物質 A.B 及 C. 若在與環
境絕熱條件下,等質量的 A 和 B 接觸,熱平衡后的溫度為 57℃;等質量的 A 與 C 接觸,熱
平衡后的溫度為 36℃. 若將等質量的 B.C 接觸,達平衡后系統的溫度應為多少?
解:設 A、B.C 的熱容各為 CA、CB、 Cc,于是有
тсA (57-80) +m св (57-40) =0(1)
mсд (36-80) +mce (36-10) =0
mcв (t-40) +m cc (t-10) =0(2)
(3)
得: cA (57-80) =-св (57-40)
CA (36-80) =-cc (36-10)(4)
(5)
Св (t-40) + cc (t-10) =0(6)
由式(4)除以式(5),解 得св=0.7995cc
將上式代入式(6)得
0.7995cc (t-40) + cc (t-10) =0
方程(7)的兩邊同除以cc,得
0.7995 × (t-40)+ (t-10) =0
解方程(8),得t=23.33℃
結果表明,若將等質量的 B、C 接觸,達平衡后系統的溫度應為23.33℃。
(7)
(8)
2-21 求 1mol N:(g)在 300K 恒溫下從 2 dm'可逆膨脹到 40 dm'時的體積功 w..
(1)假設Nz(g)為理想氣體;
(2)假設 Nz(g)為范德華氣體,其范德華常數見附錄。
解:(1)假設 Nz(g)為理想氣體,則恒溫可逆膨脹功為
W, =-nRT In(V,/V,)=-1×8.3145×300×In (40÷2)J=-7472J=7.472 kJ(2)查附錄七,得其范德華常數為
a =140.8×10-3Pa-'·m.mol?; b=39.13×10°m-3.mol
w.-f ow-i o n -m n(
=-1×8.314×300ln
-12x140.8×10(40x1032x10)
=-7452J=-7.452kJ
2-22某雙原子理想氣體1mo1從始態350K,200kPa經過如下四個不同過程達到各自
的平衡態,求各過程的功W.
(1)恒溫可逆膨脹到50kPa;
(2)恒溫反抗50kPa恒外壓不可逆膨脹;
(3)絕熱可逆膨脹到50kPA;
(4)絕熱反抗50kPa恒外壓不可逆膨脹。
解:(1)恒溫可逆膨脹到50kPa:
W=(2p)=×.1530n5x0)xJ=43/=-.3kJ
(2)恒溫反抗50kPa恒外壓不可逆膨脹
W=-Pamb(V2 -V1) =-Paumb{(nRT/ Pamb)-(nRT/ P1)=-nRT{1-(P/p1)}=-1×8.3145×3501-(50/200}J
=-2183.J=-2.183kJ
(3)絕熱可逆膨脹到50kPa:T2=()x=(×350K=235.53K
絕熱,Q=0,
W=△U=[=n×Cvm×(T2-T1)
=1×5×8.3145×(235.53-350)J=-2379J=-2.379kJ
(4)絕熱反抗50kPa恒外壓不可逆膨脹
絕熱,Q=0,W=AU
-Pabm (V2-V1)=nCvm(T2-T1)
-P(nRT2/ P)-(nRT1/p1)}=n×(5/2)R(T2-T1)上式兩邊消去nR并代入有關數據得
-T2+0.25×350K=2.5T2-2.5×350K
3.5T2=2.75×350K故
T2=275K
W=△U=[nc.or=n×Cvm×(T2-T1)
=1×5×8.3145×(275-350)J=-1559J=-1.559kJ
2-235mo1雙原子理想氣體1mo1從始態300K,200kPa,先恒溫可逆膨脹到壓力為
50kPa,再絕熱可逆壓縮末態壓力200kPa。求末態溫度T及整個過程的Q,W,△U及△H
解:整個過程如下
300K300K
T
200kPa恒溫可逆膨脹50kPa=p1絕熱可逆壓縮200kPa=P25mol5mol
5mol
RA7R/2
T=()200×10
×400K=445.80K
50×10
恒溫可逆膨脹過程:
W,=nRT Imt(p2/p)=5x8.3145×00ln|xJ=-17289J=-1.2kJ因是理想氣體,恒溫,△U=△H=0
絕熱可逆壓縮:Q=0,故
W=△U=nCv(T-T)=5xR(T-T1)
=5××8.314×(445.80-300)xJ=15153/=15.15k/
△H=nCAm(T-T1)=5×R(T-T1)
=5x÷×8.314×(445.80-300)×J=21214J=21.21kJ
故整個過程:
W=W,+W=(-17.29+15.15)kJ=2.14kJ
△U=△U+△U=(0+15.15)=15.15kJ
△H=△H,+△H=(0+21.21)=21.21kJ
2-24求證在理想氣體p-V圖上任一點處,絕熱可逆線的斜率的絕對值大于恒溫可逆
線的斜率的絕對值。
解:理想氣體絕熱可逆方程為:pV=常數=K(1)
理想氣體恒溫可逆方程為:pV=常數=C(2)
對方程(1)及方程(2)求導,得
(p1ov)a=-(pIV)(3)
(pV)=-(p/V)(4)
因y=CC>1,故在理想氣體p-V圖上任一點處,絕熱可逆線的斜率的絕對值
|-y(p/V)|大于恒溫可逆線的斜率的絕對值|-(p/V)|。
2-25一水平放置的絕熱圓筒中裝有無磨擦的絕熱理想活塞,左、右兩側分別為50dm
的單原子理想氣體A和50dm3的雙原子理想氣體B.兩氣體均為0℃、100kPa。A氣體內部有
一體積及熱容均可忽略的電熱絲.現在經通電無限緩慢加熱左側氣體A,推動活塞壓縮右側
氣體B使壓力最終到達200kPa。求(1)氣體B的最終溫度;(2)氣體B得到的功;(3)
氣體A的最終溫度;(4)氣體A從電熱絲得到的熱。
解:(1)右側氣體B進行可逆絕熱過程
T2=T1(2=273.15x(200x10)K=332.97K
(2)因絕熱,Q-0,
W.-=AV-=n.,)
100×103×50×1035×8.314
2×(332.97-273.15)×J=2738.J=2.738kJ
8.314×273.15
(3)氣體A的末態溫度
P.Y rT
nRT RTP.V,T2_100×103×50×332.97dm3=30.48.6dm3
P2P2200×103×273.15
VA=(2×50-30.48)dm2=69.52dm
TP2VA P2VAP2VAT200×103×69.52×273.15K=759.58K
nR (P1V I RT1)R PV100×103×50
(4)氣體A從電熱絲得到的熱
=2.2017mol=n
Q=△U-W=nCm(T-T)+W
=2.2017××8.314×(759.58-273.15)x103kJ+2.738kJ
=13.356kJ+2.738kJ=16.094kJ
2-26在帶活塞的絕熱容器中有4.25mo1的某固態物質A及5mol某單原子理想氣體B,物質A的C=24.454J·mol·K.始態溫度T:=400K,壓力p1=200。
今以氣體B為系統,求經可逆膨脹到p=100kPa時,系統的T:及過程的Q,W,△U及△H。(注意:以p:=50kPa解題,得不到和答案一樣的結果,可能是p:=100 kPa。估計是打印錯誤所致)
解:今以氣體B為系統:×400K=303.14K
Q=-=-1 4.25×24.454dT}J
=-[4.25×24.454×(303.14-400)]J=10067.J≈10.07kJ
△U={5.0××R(303.14-400)}J=-6040.J≈-6.04kJ
△H={5.0x÷×R(303.14-400)}J=-10067J≈-10.07kJ
W=AU-Q=-16.11kJ
2-28已知100kPa下冰的熔點0℃,此時冰的比熔化Ah=333.3J.g。水的均比定壓熱容c=4.184J-g-K。求絕熱容器內向1kg50℃的水中投入0.1kg0℃的冰后,
系統末態的溫度。計算時不考慮容器的熱容。
解:變化過程示意如下
(0.1kg,0℃冰)→( 0.1kg,0℃,水)→( 0.1kg,t,水)
( 1kg, 50℃,水)→(1kg,t,水)
過程恒壓絕熱: Q,=ΔΗ =0, 即 ΔΗ=ΔΗ,+ΔΗ,=0
100g×333.3J.g-.K-+100gx4.184J.g-.K-x(T-273.15K)
+1000×4.184J.g-1.K-1x(T-323.15K)=0
4602.4T=1433015.56K
T =311.363K,故t=38. 21℃
2-29 已知 100kPa下冰的熔點為0℃,此時冰的比熔化焓△h=333.3J-g-1.水和冰的均比定壓熱容c,分別為 4.184J-g--K-1及 2.000J-g-1.K-1.今在絕熱容器內向 1kg 50℃的水中投入 0. 8 kg 溫度-20℃的冰。求:(1)末態的溫度;(2)末態水和冰的質量。
解:過程恒壓絕熱:Q,=ΔΗ=0,即 ΔΗ=ΔΗ,+ΔΗ,=0
800g ×2.0xJ.g-.K-(273.15K-253.15K)+800g ×333.33J.g-1.K-1
+800g ×4.184J·g·K-x(T-273.15K)
+1000x4.184J.g-1.K-x(T-323.15K)=0
32000+266640-914287.68-1352059.6=7531.2T
T=261.27K
這個結果顯然不合理,只有高溫水放出的熱量使部分冰熔化為水,而維持在 0℃,所以末態的溫度為 0℃.
(2)設 0℃冰量為 m,則 0℃水量為(500-m)g,其狀態示意如下
800g,H2O(s), 253.15K0.=0(800-m)gH20(1), mH2O(s), 273.15K
1000g, H20(1), 323.15K1000g, H,O(1), 273.15K
800 g×2.J·g·K× (273.15 K-253.15K)+ (800-m) g×333.3J·g
+1000g×4.184J·gl·Kl× (273.15K-323.15K) =0
333.3 m = 89440 g
m=268g =0. 268 kg =冰量
水量= (1000+(800-268)}g=1532 g =1.532 kg
2-30 蒸氣鍋爐中連續不斷地注入 20℃的水,將其加熱并蒸發成 180℃,飽和蒸氣壓為 1.003Mpa 的水蒸氣。求每生產 1kg 飽和水蒸氣所需的熱。
已知:水(H20,1)在 100℃ 的摩爾相變焓 △H(373.15K)=40.668kJ-mol-1,水的平均摩爾定壓熱容為c,(H.0.1)=75.32J-mor1,水蒸氣(H.0,g)的摩爾定壓熱容與溫度的關系見附錄.
解:據題意畫出下列方框圖:
H2O (1), 1kg
20℃, 1000.3kPaQ=ΔΗ
H2O (g), lkg
180℃, 1000.3kPa
ΔΗΔΗ2
H2O (1), 1kg
100℃, 101.325kPa1000x40.668kJ=2259kJ
18HO (g), 1kg
100℃, 101.325kPa
1000
Δ Hi =mH,ou)Cpm(12 -1) =×75.32× (100-20)J=334.76J
18
1000 53.15
ΔΗ2='nCp.H,08dT =((29.16+14.49×10-T/K
18 73.15K
-2.002×10°T2/K2)dTIKkJ=154.54kJ
所以每生產 1kg飽和蒸氣所需的熱
Qp=ΔH=ΔHi+△ vapHg (373.15K) +ΔH2=
= (334.76+2257+154.54) kJ=2.746 ×10kJ
2-31 100kPa 下,冰(H0,s)的熔點為 0℃,在此條件下冰的摩爾熔化焓△H=6.012kJ-mol-'.已知在-10℃~0℃ 范圍內過泠水(H:0,1)和冰的摩爾定壓熱容分別為 C,..(H:0, 1)=76.28J-mol--K-1和C,..(H.0, s)=37.20J-mol-1-K-1.求在常壓下及 -10℃下過冷水結冰的摩爾凝固焓。
解:
H2O(1),-10°C H2O(s),-10°C
ΔΗ.|ΔΗ.
H20(1), 0°CAH H2O(s), 0°C
ΔΗ =-ΔΗ =-6.012kJ .mol-
ΔΗ =ΔΗ + ΔΗ2+ΔΗ
73.15A5
263.1SK,Cp(H,O,I)dT +ΔH2m+ 73.15K Cpm(H,O,s)dT
=C,(H,0./)x(273.15K-263.15K)
+ΔΗ2 +C,(H,O,s)x(263.15K-273.15K)
=(76.28×10-6012-37.2×10)J·mol-
=-5621J-mol =-5.621kJ.mol
2-32 已知水(H20,1)在 100℃的摩爾蒸發焓△H=40.668kJ·mol-',水和水蒸氣在 25~100 ℃的平均摩爾定壓熱容分別為Cpm(H,O,1)=75.75 J-mol--K-1和Cpm(H2O,g)=33.76 J·mol-'·K-'。求在 25℃時水的摩爾蒸發焓。
解:H2O(1),25°C
ΔH..ΔΗ
H2O(g), 25°C
ΔΗ.
H,O(I), 100°CΔΗ
H2O(g), 100°C
ΔΗ, = ΔΗ + ΔΗ + ΔΗ
5 Cm(H2O,I)dT +ΔH 2+ SC(H2O,s)dT
=Cp.n(H,O,1)×(373.15K-298.15K)
+ΔpHm+C,(H,0,g)x(298.15K-373.15K)
= (75.75x75+ 40668-33.76x75)J·mol
=-43817J·mol-'=-4.3821kJ·mol-
2-33 25℃下,密閉恒容的容器中有 10g 固體萘 CioHs(s) 在過量的 0z(g) 中完全燃
燒成 COz(g)和 H20(1),過程放熱 401.727 kJ.求
(1) CH,(s)+1202(g)=10CO2(g)+4H,0(1)的反應進度;
(2)CtoHe(s)的△CU; (3)CioHls(s)的△cH°.
解: (1)反應進度: ξ=△n/v=△n/1=An=128J72=0.078019mol =78.019mmol
(2)CroHs(s)的△cU°: Mx=128. 173
每摩爾蔡的恒容恒溫燃燒熱為
Δ.υ(298.15K) = Δ.U(298.15K) = 128.173 x (-401.727)kJ - mol"
=-5149kJ·mol
(3)所以本題所給反應的標準摩爾反應焓為
Δ,Η(298.15K) = Δ,υ(298.15K)+ Σνα(g).RT
=(-5149kJ + (-2)×8.314 × 298.15×10')kJ·mol
=-5154kJ · mol
ΔΗ° = Δ,Η° = -5154kJ- mol""
2-34 應用附錄中有關物質在 25℃的標準摩爾生成焓的數據,計算下列反應的
Δ,Η°(298.15K) Δ,U(298.15K).
(1) 4NH, (g) +50; (g)= 4NO (g) +6H,0 (g)
(2) 3NOz (g)+ H20 (1)= 2HNO, (1) +NO (g)
(3) Fe:0;(s)+3C(石墨)=2Fe (s) +3C0 (g)
解:計算公式如下:
Δ,Η° =Σν, Δ,Η°(Β, β,T): Δ,U° = Δ,Η°-Σν,(8)- RT
(1) Δ,Η°(298.15Κ)= (4x90.25+6x(-241.818)-4x(-46.11)kJ-mol-
=-905.468kJ ·mol-1 =-905.47kJ-mol
Δ.U(298.15K) =(-905.47-1x8.3145x298.15x10-)kJ-mol- =-907.95kJ-mol-
(2) Δ,Η°(298.15K)= {2x(-174.10)+90.25-(3x33.18-285.83)}kJ-mol-1
= -71.66kJ·mol
Δ,υ (298.15K) =(-71.66-(-2)x8.3145x298.15x10-3kJ -mol- =-66.70kJ - mol-(3) Δ,H°(298.15K)= (3x(-110.525)-(-824.2)}kJ-mol-= 492.63kJ-mol-
Δ.υ(298.15K) = (492.63-3x8.3145x 298.15x10-kJ-mol- = 485.19kJ -mol
2-35 應用附錄中有關物質的熱化學數據,計算 25℃時反應
2CH,OH(1)+02(g) =HCOOCH,(1)+2H,0(1)
的標準摩爾反應焓,要求:(1)應用 25℃的標準摩爾生成焓數據;
△,H°(HCOOCH,,1)=-379.07kJ·mol'。(2)應用 25℃的標準摩爾燃燒焓數據。
解:(1) 2CH,OH(I)+O2(g)= HCOOCH,(1)+2H20(1)
Δ,Η° =2xΔ,Η°(H,O,)+Δ,H°(HCOOCH,,1)-2xΔ,H°(CH,OH,I)
= {2× (-285.830) + (-379.07) -2× (-238.66)} kJ· mol"
- 473.52 kJ·mol"
(2) Δ,H°=2xΔH°(CH,OH,1)-ΔH°(HCOOCH,,/)
- 473.52 kJ·mol
{2× (-726.51)-(-979.5)} kJ·mo1"
2-36 (1)寫出同一溫度下下,一定聚集狀態分子式為 C.Hz的物質的△,H°與其△.H°
之間的關系。
(2) 若 25℃下環丙烷C.CH.CH(g)的 △.H°=-2091.5kJ-mol-1,求該溫度下環丙
烷的△,H
解:(1)C.Hz。的物質進行下述反應:
C,H2n+4nO(g)=nCO2(g)+nH202
Δ.H°(C,H2,)=Δ,H°=ΜΔ,H°(H2O,/)+nΔ,H°(CO28)-Δ,H°(C,H2,)
故有Δ,H°(C,H2,)+Δ,H°(C H2)=?Δ,H°(H,O,1)+Δ,H°(CO28))
(2)常壓恒定溫度 25℃的條件下,環丙烷進行下述反應:
CH.CH, CH+10,(8)=3C0(8)+3H,00)
Δ,Η(298.15kK) = 3Δ,Η(CO2,298.15kK)
+3△,H°(H,0,1,298.15kK)-△,H°(環丙烷,g,298.15kK)
:△,H°(環丙烷,g,298.15kK)=3△,H°(CO2,g,298.15K)
+3Δ,Η(Η,0,1,298.15Κ)-Δ,Η(298.15K)= (3x(-393.51) +3x (-285.83) -(-2091.5) }kJ·mol-1 =53.48kJ ·mol-2-37 已知 25℃ 甲酸乙酯(HCOOCH,1)的標準摩爾摩爾燃燒焓 △.H°為-979.5
kJ·mol-',甲酸乙酯(HCOOCH,,1)、嚼(CH,OH,1)、水(H:0,1)及二氧化碳(CO,,g)
的標準摩爾生成焓數據△,H°分別為-424.72 kJ·mol-', -238.66 kJ·mol-1,
-285.83 kJ.mol-及-393.509kJ.mol-.應用這些數據求25℃時下列反應的標準摩爾反應
焓。HCOOH(I)+CH,OH(I)=HCOOCH,(I)+H2O(1)
解:(1)先求△,H°(HCOOCH,,I)
HCOOCH,(1)+202(g)=2CO2(g)+2H20(1)
Δ,Η° = 2xΔ,Η°(CO2,8) + 2x Δ,Η°(H,0,/)-Δ,Η°(HCOOCH,,1)
Δ,H°=ΔH°(HCOOCH,,I)
所以有
Δ,H°(HCOOCH,,I)=2xΔ,H°(CO2,8) +2x Δ,H°(H,O,1)-ΔH°(HCOOCH,,1)
= {2× (-393.509) +2× (-285.83) - (-979.5)} kJ·mol"
=- 379.178 kJ·mol
(2) HCOOH(I)+CH,OH(I)=HCOOCH,(I)+H2O(1)
Δ,Η° = Δ,Η°(HCOOCH,,1)+Δ, H°(HO,,1)
-Δ,H°(HCOOH,I)-Δ,H°(CH,OH,I)
= {(-379.178) + (-285.83) - (-424.72) - (-238.66)} kJ - mol"
=-1.628 kJ ·mol
2-38 已知 CH,COOH(g),COz(g)和 CH.(g)的平均定壓熱容 Cp.m分別為 52.3 Jmol·K',
31.4 J·mo1·K1,37.1 J·mo1·K'.試由附錄中各化合物的標準摩爾生成焓計算 1000K
時下列反應的△,H°
CH,COOH (g) =CH. (g) +CO2 (g)
解:由附錄中各物質的標準摩爾生成焓數據,可得在 25℃ 時的標準摩爾反應焓
Δ,Η°(298.15K)=Σν Δ,Η(298.15Κ)
=(-74.81-393.51-(-432.2)JkJ-mol-=-36.12kJ-mol-
題給反應的Δ,Cm =
SvC p.m.84-(37.7+31.4-52.3) J. mo1·K= 16.8J · mol·K
所以,題給反應在 1000K 時的標準摩爾反應焓
Δ,Η(1000Κ) = Δ,Η(298.15Κ)+AO
osk. A,C,dT
=(-36. 12+16.8x (1000-298. 15) x10)kJ . mo1= -24. 3kJ . mol
2-39 對于化學反應CH4(g)+H20(g)= CO(g)+3H2(g)
應用附錄中各物質在 25℃時標準摩爾生成焓數據及摩爾定壓熱容與溫度的函數關系
式:(1)將△,H"(T)表示成溫度的函數關系式;
(2)求該反應在1000K時的△,H.
解:為求 △,H(T)的溫度函數關系式,查各物質的定壓摩爾熱容為
H: C=26. 88J ? mol"? K"+4. 374 x 10"J ? mo1?K"-0. 3265 x 10*J ? mo1"?KCo: C=26. 537J mo1K+7.6831 x 10J mo1K-1. 172 x 10J mo1KH0 (1): C=29.16J molK+14. 49 x 10JmolK-2. 022x 10Jmo1K
CH. (g): C-14.15J molK+75.496x10J.mo1K-17.99x10J.mo1.K
Δα =Σνα,=63. 867 J- mol -K';
Ab=Σvab= - 69. 2619 J ? mol-K
Δc =VnC = - 69262 J · mol-K
再查298.15K 時的各物質的標準摩爾生成焓,求 △,H°(295.15K):
Δ,Η°(295.15K)=Δ,Η°(CO,8)-Δ,Η°(H20,8)-Δ,Η°(CH,8)
={(-110.525) -(-74. 81)-(-241.818)} kJ·mo1=206.103 kJ·mo1
根據基希霍夫公式
Δ,Η°(Τ)-Δ,Η°(295.15K)+A,CdT
298.15K
=Δ,Η°(295.15K)+ 5 (Δa + ΔbT + ΔcT)dT
-Δ,Η° (295.15Κ)+ Δα(Τ - 298.15)+Δb(Τ2 - (298.15))-Δb(Τ' - (298.15)')將△,H°(295.15K),△a,△b,△c 的數據代入上式,并整理,可得
Δ,Η(T)= (189982+63. 867 (T/Κ)
-34.6310×10 (T/K) +5.9535 × 10* (T/K) }J·mol
(2)將1000K代入上式計算得
Δ,Η(T)= 225. 17 k J. mo1
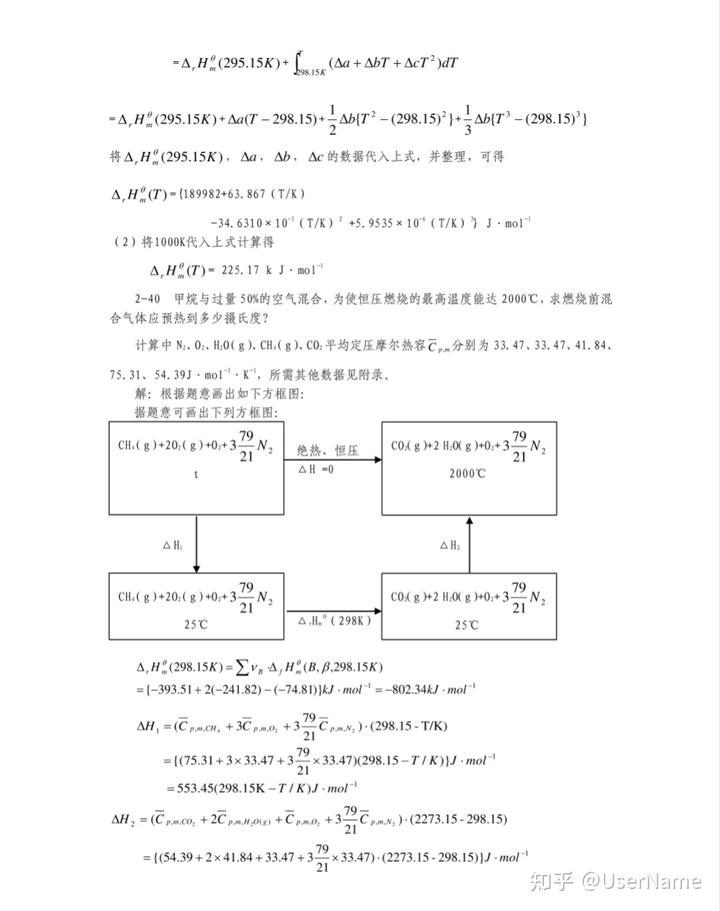
2-40 甲烷與過量 50%的空氣混合,為使恒壓燃燒的最高溫度能達 2000℃,求燃燒前混
合氣體應預熱到多少攝氏度?
計算中 N、02、H0(g)、CH.(g)、CO:平均定壓摩爾熱容C分別為 33.47、33.47、41.84、
75.31、54.39J·mol”·K',所需其他數據見附錄。
解:根據題意畫出如下方框圖:
據題意可畫出下列方框圖:
CH.(g)+20,(g)+0+372 N絕熱、恒壓
COAg )+2 H.0( g)+0+3N2
ΔΗ =0ΔΗΣ
2000℃
ΔΗ
CH.(g)+20;(g)+0;+32N2C0A g +2 H.0( g)+0++372N2
25℃25℃
Δ,Η°(298.15Κ)= Σν. Δ,Η(Β. β.298.15Κ)
=(-393.51+2(-241.82)-(-74.81)}kJ·mol- =-802.34kJ ·mol-
ΔH, =(Cpm.cH. +3Cpmo, +37Cm,).(298.15-T/K)
=((75.31+3x33.47+37x 33.47)(298.15-T/K))/- mot
=553.45(298.15K-T/K)J·mol-
ΔΗ, = (Cmco, + 2Cm,o) +Coma, +372Cmx.)-(2273.15-298.15)
ΔΗ.°(298K)
= (54.39+2x41.84+33.47+37 x 33.47)-(2273.15- 298.15)J -mol
1084.81kJ·mol
: ΔΗ = ΔΗ, + Δ,Η(298.15Κ)+ ΔΗ, = 0
即553.45 (298.15-T/K) ×10+ (-802.34) +1084.81=0
所以T-808.15K 或 t=535℃.
2-411mo1H2與過量 50%空氣的混合物的始態為 25℃、101.325kPa.若該混合氣體于容器
中發生爆炸,試求所能達到的最高溫度和壓力。設所有氣體均可按理想氣體處理,H20(g)
0z及 Nz的Cv.m分別為37.66、25.1 及 25.1J·mol".K1.
解:據題意可畫出下列方框圖:
H,(g)+0.50:(g)+0. 250+0.75N
25℃, 101.325kPaΔU =0
絕熱、2H:0(g)+0.250:+0.75N2
恒容t, p
△,U. (298K)AU,
2H.0(g)+0.250:+0.75N
25℃
ΔU(298.15K)= Δ,Η-Σν(g)- RT
=Δ,Η°(Η,0, g,298K)-Σν(g). RT
=(-241820-(-0.5×8.314× 298.15)}J-mol-
=-240581J ·mol-
ΔU, = (Cvmo) +0.25Cv.o, +0.7572Cv..).(T/K - 298.15)= ((37.66 + 0.25 x 25.1+ 0.75x25.1).(T/K-298.15)J -mol= 114.753(T /K - 298.15)J mol-1
: ΔU = Δ,U(298.15K)+ ΔU, =0
E -240581=11.753 (T/K-298. 15)
所以n.s =(1+0.25+0.75x) mol = 4.0714mol
n. =(1+0.75+0.75x) mol=4.5714mol
T=298.15K, p=101. 325kPa
P始態V =ng.始態·RT始態
pV=ng.末志·RT未態解得:T=2394.65K
p=XP=4.5714x298.15
4.0714×2394.65
-x101.325kPa = 724.5kPa2-42 容積恒定的帶有二通活塞的真空容器置于壓力恒定、溫度 T。的大氣中。現將二
通活塞打開,使大氣迅速進入并充滿容器,達到容器內外壓力相等。求證進入容器后大氣的
溫度 T= γ To.Y 為大氣的熱容比。推導時不考慮容器的熱容,大氣按一種氣體對待。提示:全部進入容器的氣體為系統,系統得到流動功。
解:真空容器終態溫度為 T,終態時進入容器內的空氣原來在容器外時所占的體積為
V(1)選取最后進入容器內的全部氣體為系統,物質的量為 n.終態時的界面包括了此
容器內壁所包圍的空間V;始態時的體積為V+V,(始態時界面內包括了一部分真空空間V).
(2)實際上大氣流入真空容器時并不作功,但大氣進入容器內是由于其余的外界大氣對其
壓縮作功的結果,這種功叫流動功.壓縮過程中,環境以恒外壓 po將界面內的體積壓縮了
△V=V- ( +V) = - o
所以,環境所作的功為
W = - poΔV = pVo= nRT(a)
由于大氣流入真空容器的過程進行得很快,可以看作是絕熱過程,由熱力學第一定律可
得AU = nCy(T-T) = W = poVo =nRT,
Cv(T-T)=RT,(b)
(4) 把大氣當作理想氣體,就有
Cp.m-Cy=R
Cp/Cvm =y
聯立求解得Cy=R/(y-1)
(c)
將式(c)代入(b)得R(T-T)=RT
y-1
所以T=To
第三章熱力學第二定律
3-1卡諾熱機在T-600K的高溫熱源和T:-300K的低溫熱源間工作,求:
(1)熱機的效率;
(2)當環境作功-W=100kJ時,系統從高溫熱源Q及向低溫熱源放出的-Q:
解:(1)n=-W/Q1=(T1-T2)/T1=(600-300)/600=0.5(2)-W/Q1=100kJ/Q1=0.5,得Q1=200kJ
Q1+Q2=-W=100kJ,Q-(-W)=-Q2=100kJ
3-2卡諾熱機在T:=795K的高溫熱源和T:=300K的低溫熱源間工作,求
(1)熱機的效率;
(2)當從高溫熱源吸熱Q=250kJ時,系統對環境作的功-W及向低溫熱源放出的-Q:
解:(1)n=-W/Q1=(T1-T2)/T1=(750-300)/750=0.6(2)-W=nQ=0.6×250kJ=150kJ
1+2=-W=150kJQ1-(-W)=-Q2=100kJ
3-3卡諾熱機在T=900K的高溫熱源和T:=300K的低溫熱源間工作,求
(1)熱機的效率;
(2)當向低溫熱源放出的-Q:=100kJ時,從高溫熱源吸熱Q及對環境作的功-W
解(1)n=-W/Q1=(T1-T2)/T1=(900-300)/900=0.6667(2)-W/Q1=0.6667(a)
Q-100kJ=-W(b)
聯立求解得:Q=300 kJ; -W-200kJ
3-4試證明:在高溫熱源和低溫熱源間工作的不可逆熱機
與卡諾熱機聯合操作時,若令卡諾熱機得到的功W等于不可逆
熱機作出的功-W,假設不可逆熱機的熱機效率n大于卡諾熱-Qi
機的熱機效率n,其結果必然有熱量從低溫熱源流向高溫熱源,W
W=-W
不可逆可逆
而違反熱力學第二定律的克勞修斯說法。熱機
熱機
解:由題意可知:在高溫熱源和低溫熱源間工作的不可逆熱機-2:
ir與卡諾熱機r,如上圖所示。調節卡諾熱機得到的功W等于T2
不可逆熱機作出的功-W。可逆熱機R從高溫吸熱Q,作功W,放熱-Q,到低溫熱源
T:,其熱機效率為,=_W。不可逆熱機ir從高溫熱源吸熱Q1,放熱-Q2到低溫熱源,
Q
其熱機效率為n=
先假設假設不可逆熱機的熱機效率n大于卡諾熱機的熱機效率n,即
n>n,或>
因W=-W,可得Q>-Q
今若以不可逆熱機i帶動卡諾熱機,使卡諾熱機r逆向轉動,卡諾熱機成為致冷機,所
需的功W,由不可逆熱機i供給,如上圖所示。卡諾熱機從低溫熱源吸熱Q,并放熱-Q
到高溫熱源。整個復合機循環一周后,在兩機中工作的物質恢復原態,最后除熱源有熱量交
換外,無其它變化。
從低溫熱源吸熱:1+21>0
高溫熱源得到的熱:(21+21)
總的變化是熱從低溫熱源傳到高溫熱源而沒有發生其它變化。顯然,這是違反熱力學第二定
律的克勞修斯說法。(所以最初的假設n>不能成立,因此有:≤,這就證明了卡諾
定理里)
3-5高溫熱源T:-600K,低溫熱源T:-300K。今有120kJ的熱直接從高溫熱源傳給低溫
熱源,求此過程的△S
解:在傳熱過程中,
高溫熱源的△S1:AS1=-120000J=-200JK
T 600K
低溫熱源的△S2:AS2==12000=400J-K
整個過程的熵變:AS=AS1+AS,=(-200+400)JK-=200JK-
3-6不同的熱機工作于T:=600K的高溫熱源及T:=300K的低溫熱源之間。求下列三種情況下,當熱機從高溫熱源吸熱Q:=300kJ時,兩熱源的總熵變△S
(1)可逆熱機效率n=0.5;(2)不可逆熱機效率n=0.45;
(3)不可逆熱機效率n=0.4
解:(1)n=Q1-02
=0.5
Q1-Q2=0.5Q1得
Q,=-150kJ
高溫熱源的△S1:△S1=
.-300kJ=-0.50kJ.K=-500J.K
T.600K
低溫熱源的△S:A=0.5kJ.K=50J.K
整個過程的熵變:AS=AS1+AS2=(-50+50)J·K=0J·K=0
(2)n=1-02=0.45
Q
Q1-Q:=0.45Q1得
Q2=-165kJ
高溫熱源的△S1:AS=Q-300kJ=-0.50kJK=-500J.K
T.600K
低溫熱源的△S:
As.0
165kJ=0.55kJ-K=550J-K
300K
整個過程的熵變:AS=AS1+AS2=(-500+550)J·K=50J·K
(3)n=0-0=0.40
Q-2=0.400得
Q=-180kJ
高溫熱源的△S1:4s,-300k1
=-0.50kJK=-500.JK
600K
低溫熱源的△S1:AS,=-Q.2180kJ=0.60kJK=600JK
300K
整個過程的熵變:AS=AS1+AS2=(-500+600)JK=100J-K-
3-7已知水的比定壓熱容c=4.184J·K·g今有1kg,10℃的水經下述三種不同
過程加熱成100℃的水。求各過程的△S,△S及△S
(1)系統與100℃熱源接觸;
(2)系統先與55℃熱源接觸至熱平衡,再與100℃熱源接觸;
(3)系統先與40℃、70℃熱源接觸至熱平衡,再與100℃熱源接觸;
解:(1)以水為系統,環境是熱源
△Sm=dT=mc,In(T2/T1)
=(1000×4.184×1n(373.15/283.15))J·K=1154.8 J·K=1155 J·K-Ime,or-mc,(T2-T)
AS
amb7
Tamt
--1000×4.184(373.15-283.15J.K-=-1009 J. K
373.15
AS =AS+ASm= (1155+(-1009)} JK=146JK
(2)整個過程系統的△S
AsS,=I m r=me,,IT)
-(1000×4.184×1n(328.15/283.15))J·K=1154.8 J·K=1155 J·K
系統先與55℃熱源接觸至熱平衡時ASamb.l
-I'me,oir-mc (T2-T)
AS.Iam.
.
-1000×4.184(328.15-283.15J.K---573. 76 JK
328.15
與100℃熱源接觸至熱平衡時ASamb.2
-I'me,ar-mc(T2-T1)
AS
amb.2.!
Tant I
-1000×4.184(373.15-328.15J.K-1=-504.57J·K
373.15
整個過程的△Sa
AS amb=AS amtb.1+AS amtb.2={-573.76+(-504.57)}=-1078JK所以,AS=ASs +ASamb=1155+(-1078)}J·K=77J·K(3)整個過程系統的△S
AsS.-=f+o ar+ar =dT = mc, In(T2 /T)
=(1000×4.184×1n(328.15/283.15)J·K=1154.8 J·K=1155 J·K
系統先與40℃熱源接觸至熱平衡時ASamb.1
-me or-mc,(T2-T1)
AS
amb.IT
amb.I.!
-1000×4.184(313.15-283.15
J.K-400.83 JK
313.15
再與70℃熱源接觸至熱平衡時ASamb.2
-I'me,ar-me(2-7)
AS
,2,.!
-1000×4.184(343.15.15-313.15.15J.K-=- 365. 88 J K
343.15
最后與70℃熱源接觸至熱平衡時ASamb.3
-I'me,or-mc,(T2-T)
AS
amb.3T
umb.Tumba
=J-1000×4.184(373.15.15-343.15.15J.K=-336.38 J·K
373.15
整個過程的△Samb
AS amt-AS+AS amb.2+AS amb 3
={-400.83+(-365.88)+(-336.38)}=-1103J·K所以,ASt=AS+ASm=(1155+(-1103)}J·K=52J·K3-8已知氮氣(N2,g)的摩爾定壓熱容與溫度的函數關系為
C=(27.32+6.226 ×103(T/K)-0.9502 ×10(T/K)3)J mo1 K
將始態為300K,100kPa下1mol的N(g)置于1000K的熱源中,求下列二過程(1)經恒
壓過程;(2)經恒容過程達到平衡態時的 Q,△S 及 △ Saabe
解:(1)經恒壓過程時:
Q=0, = ΔΗ =A0k CpdT
將 C,.a代入上式積分得
2,-(27.32× (1000-300)+6.226×10× (1000'-300°)
0.9302 x10*x (1000'-300') )J= 21648 J = 21.65 kJ
2
AS = CaT
將 C,。代入上式積分得
AS= (27.32 × In (1000/300) +6.226 ×10-× (1000-300)
-(0.9502/2) ×10?x (10002-3002)} J·K
= (32.893 + 4. 3582 - 0.4323) JK= 36.819 J-K= 36.82 J- K1
(2)如果把氮氣看作是理想氣體,則有Cpm-R=CyJm
2=2=ACT= (C-R)dT=CT- RaT
根據前一步計算,CdT =26. 15 kJ
0 RdT= (8. 314× (1000 -300)} kJ= 5.82 kJ
而
所以, Q= (26.15 -5.82 ) kJ = 15.83 kJ
AS = C= R=-
由(1)計算可知,CT = 36.82 J -K
A000K RdT = {8.314xIn(1000/300)} J·K = 10.01 J-K
OOK T
所以ΔS = {36. 82 - 10. 01} J·K = 26.81 J- K
3-9始態為T=300K, p=200kPa的某雙原子氣體1 mol,經下列不同途徑變化到
T:=300K, px=100 kPa 的末態。求各步驟及途徑的 Q,△S.
(1)恒溫可逆膨脹:
(2)先恒容泠卻至使壓力降至 100kPa,再恒壓加熱至 Ta;
(3)先絕熱可逆膨脹到使壓力降至 100kPa,再恒壓加熱至 Tz;
解:(1) 恒溫可逆膨脹,dT =0, △U=0,根據熱力學第一定律,得Q=-W =-nRT In(p2/pi)
= (- 1×8. 314 × 300 × 1n (100/200)} J = 1729 J=1.729 kJ△S =-nRIn(p2/pi)
= {- 1×8.314× In (100/200)} J·K- = 5.764 J·K
(2)過程為
Imol雙原子氣體1mol雙原子氣體
1mol雙原子氣體
T, =300K, V,To, V,
T, = 300K
p, = 200kPaPo =100kPa
p2 = 100kPa
恒容恒壓加熱
根據理想氣體狀態方程,得
To=(po/p,)×T= {(100/200) × 300) K= 150K
第一步驟,恒容: dV=0,W,=0,根據熱力學第一定律,得
A50
Q, = ΔU, =ook"CydT
= (1x (5/2) ×8. 3145 × (150-300)} J= -3118 J = -3. 118 kJ
AS, =nCyIn(T,/T,)= {1x(5/2)×8.314xIn(150/300)) J.K- = -14. 41 J.K-
第二步:
Q2 = ΔΗ =soxnC,dT
= {1× (7/2) × 8. 3145 x (300-150)} J= 4365 J = 4. 365 kJ
ΔS2 =nC, In(T, IT)= (1x(7/2)×8.314xIn(300/150)} J.K = +20. 17 J.K-1
Q= Qι + Q = {(-3. 118) + 4. 365 ) kJ = 1. 247 kJ
AS = AS + ΔS = {(-14.41) + 20. 17) J- K = 5. 76 J- K
(3)第一步驟為絕熱可逆,故
To=(po/p,)R/Cp xT, ={(100/200)2/7×300}K =246.1K
Q.,=0, AS=(8Q, IT)=0
Q: = ΔΗ = K nCdT= {1x (7/2) x 8. 3145 x (300-246.1)} J= 1568 J = 1. 568 kJAS, =nC, In(T, IT)= (1x(7/2)x8.314xIn(300/246.1)} J.K = +5.76J .K
Q=Qi+Q2= (0+ 1.568} kJ= 1.568 kJ
AS= AS + ΔS2 = (0+5.76) J.K=5.76J.K
3-10 1 mol 理想氣體 T=300K 下,從始態 100 kPa 經下列各過程,求 Q,△S 及 △Siso
(1)可逆膨脹到末態壓力為 50 kPa;
(2)反抗恒定外壓 50 kPa 不可逆膨脹至平衡態;
(3)向真空自由膨脹至原體積的兩倍。
解:(1) 恒溫可逆膨脹,dT=0,△U=0,根據熱力學第一定律,得
Q=-W=-nRT In(p2/p)
= (- 1× 8. 314 × 300 × 1n (50/100)} J = 1729 J=1. 729 kJ
AS =-nRIn(p2/pi)
= (-1× 8. 314 × In (50/100)} J.K = 5. 764 J.K1
ASamb =-Qm ITamb= (17290/300)J·K=-5.764 J·K
故△S=0
(2)△U=0,
Q1--W punt(V1-V.)=((nRT/)-(nRT/pi)= nRT( 1-( pamb / p)}
={-1×8.314×300×(1-0.5)}J=1247J=1.247kJAS=-nRIn(p2 P1)
={-1×8.314×1n(50/100)}J·K-1=5.764J·KAS amb =-Qy ITmb = (-1247÷300) J. K=-4.157 J· K△S = △S + △S = (5.764 +(-4.157)) J.K=1.607 J·K
(3)△U=0,W=0,Q-0
AS amb=-/T
因熵是狀態函數,故有
AS=nRln(V2 /V1)=nRln(2V1 /V1)
=(1×8.314×1n2 }J·K=5.764 J·K
AS s= ASsys +ASb= 5. 764 J K
3-11某雙原子理想氣體從T=300K,p=100kPa,V=100dm'的始態,經不同過程變
化到下述狀態,求各過程的△S.
(1)T:=600K, V- 50 dm';(2)T:=600K, p= 50 kPa;
(3)p=150 kPa,V=200 dm;
解:先求該雙原子氣體的物質的量n:
(1)AS=nCIn(T2/T1)+nRIn(V2/V1)
={4.01xIn+4.01×RIn]J-K=34.6J·K
(2)AS=nCm In(T2/T1)-nRn(P2/P1)
={4.01xn-4.01xRIn}J.K-103.9J·K
(3)AS=nCm In(P2 / P1)+nC pm In(V2 /V1)
={4.01×In+4.01×In}JK=114.65 J-x
3-122mo1雙原子理想氣體從始態300K,50dm,先恒容加熱至400K,再恒壓加
熱至體積增大至100m3,求整個過程的Q,W,△U,△H及△S
解:過程為
2mol雙原子氣體2mol雙原子氣體
2mol雙原子氣體
T=300K恒客加熱
T=400K
恒壓加熱
T2=?
50dm3, Pi50dm3,po
100dm3,Po
p1=2RT/V1={2×8.3145×300/(50×10-3)}Pa=99774Pa
Po=p1To/T1={99774×400/300}Pa=133032Pa
T2=PoV2/(nR)1={133032×100×103/(2×8.3145)}K=800.05K
W-0; W--pab (V2-V)=(-133032 ×(100-50) ×10}J=-6651.6 J
所以,W=W:=-6.652kJ
△H=nC(T2-T1)={2xRx(800.05-300)}J=29104J=29.10kJ
AU=nCm(T2-T1)={2×R×(800.05-300)}J=20788J=20.79kJ
Q=△U-W=(27.79+6.65)kJ=27.44 kJ
△S=△S2+△S,=nC,_n+nC,ln
=2xRin+2xRin
800.05)JK=52. 30 JK
400
3-134mo1單原子理想氣體從始態750K,150kPa,先恒容冷卻使壓力降至50kPa,再
恒溫可逆壓縮至100kPa。求整個過程的Q,W,△U,△H,△S.
解:過程為
4mol單原子氣體4mol單原子氣體
4mol單原子氣體
T=750K恒容冷卻
To=?
可逆壓
T:=To
V,P1=150kPaV1,Po=50kPa
V2,100kPa
To=T1p0/p1={50×750/150}K=250KW=0,
W=W2=nRTIn(p2/p0)={4×8.3145×250In(100/50)}J=5763J=5.763kJ△U2=0,△U=△U1={4xR×(250-750)}J=-24944J=-24.944kJ
△H2=0,△H=△H1={4×R×(250-750)}J=-41570J=-41.57kJ
Q=△U-W=(-24.944-5.763)kJ=-30.707 kJ≈30.71 kJ
△S=△S,+△S=nCln一nnP
={4x3Rln250-4×Rn100)JK=-77.86 JK
75050
3-143mo1雙原子理想氣體從始態100kPa,75dm,先恒溫可逆壓縮使體積縮小至50
dm,再恒壓加熱至100dm。求整個過程的Q,W,△U,△H,△S.
解:過程為
3mol雙原氣體3mol雙原子氣體
3mol雙原子氣體
V=75dm3恒溫可逆壓縮
Vo=50dm
恒壓加熱
V,=100dm
TI,P1=100kPaTi,po=?
T2,P0=P2
T1=p1V1/(nR)={100×103×75×10-3/(3×8.3145)}K=300.68K
Po =nRT, /Vo =(3×8.3145×300.68/(50×10-3)JK=150000Pa=150kPa
T2 = p2V2 /(nR)=(150x103x100x103/(3x8.3145)IK=601.36K
W=W, +W, =-nRT, In(Vo /V,)-po(V2-Vo)
=(-3×8.3145×300.68In(50/75)-150×103×(100-50)×10-3)J
=-4459 J =- 4. 46 kJ
ΔU, =0, ΔU =ΔU, = (3xRx(601.36-300.68))/ = 18750/ = 18.75k
ΔΗ, =0, ΔΗ= ΔΗ, =(3xRx(601.36-300.68))J = 26250J = 26.25k)
AS =AS,,+AS, =-R InP+nC,n
Q= ΔU - W = (18. 75 + 4. 46 ) kJ = 23.21 kJ
(-3xRxIn 150+3xRim 601.36) J.K= 50.40 J. K
3-15 5 mol 單原子理想氣體從始態 300 K, 50kPa,先絕熱可逆壓縮至 100 kPa,再恒
壓冷卻使體積縮小至 85 dm',求整個過程的 Q, w, △U, △H, △S.
解:過程示意如下:
5mol 單原子氣體5mol 單原子氣體
V, =?,T, = 300K,絕熱可通壓縮恒壓冷卻熱
Vo =? ,To,5mol 單原子氣體
p, = 50kPaPo =100kPa
V2 = 85dm',T2, P2
To =(po/p,)RCT,={(100/50)2/5 x300)K =395.85K
Vo = nRT, /po =(5×8.3145×395.85/(100×10°)}m'=0.16456m
2.=0, W,=△U, =(5xRx(395.85-300)}/=5977J=5.977k
T,=P:V_100000× 0.085
nRе)K = 204.47K
5×8.314
W = - pas ( V: - V,) = (- 100 × 10'× (85 - 164.56) × 10°) J = 7956 JW = W, + W, = 13933 J = 13.933 kJ
ΔU, = (5x Rx(204.47-395.85))J =-11934J
ΔU = ΔU, + ΔU, = -5957 J = - 5.957 kJ
ΔΗ =(5xRx(204.47-300))/ =-9929J=-9.930k
Q=Q2=△U-W, =(-11.934-7.956)kJ =-19.89kJ
AS =AS.,+AS, =0+nC, In(7, /7.)= (5xRxlm 204.47.- =-68.66/-K
3-16 始態 300 K,1Mpa 的單原子理想氣體 2 mol,反抗 0. 2 Mpa 的恒定外壓絕熱不
可逆膨脹平衡態。求整個過程的 W, △U, △H, △S.
解:Q = 0, W = △U
-P (V-V)=nxR(T -T,)
-T--τ
代入數據整理得 5T,= 3.4 T,= 3.4 × 300K; 故 T2=204 K
W=ΔU,=(2xRx(204-300))J =-2395J =-2.395J
ΔΗ =(2xRx(204-300))/=-3991=-3.991kJ
AS=C-R
=(2xRxin 204-2xRin.κ
=(-16.033+26.762)J.K-=10.729J-K-=10.73J.K-1
3-17 組成為 y(B) = 0.6 的單原子氣體A與雙原子氣體 B的理想化合物共 10 mo1,從始態 T, =300K,pi =50kPa,絕熱可逆壓縮至 p;=200 kPa 的平衡態。求過程的 W, △U,△H, △S (A), △ S (B).
解:先求混合物的摩爾定壓熱容
C=C(B)=0.6xR+0.4xR=3.IR
T2 =(p:/p,)RCT, =((200/50)/×300)K =469.17K
ΔΗ = (10×3.1Rx(469.17-300)}J = 43603J= 43.60kJ
Cymmis=Cp.mmis=R=2.1R nx= yxn = 0.4×10mol = 4mol ng =6mol
ΔU = (10x2.1Rx(469.17-300)J =29538J = 29.54kJ
Pв.i=УsP,=0.6×50kPa =30kPa, PA,=20kPa
Pв.2 =У,P2 =0.6×200kPa =120kPa, PA2=80kPa
AS(A)=C(A)-,Rin =(4xx 4387-4xR-x
= (37.18-46.105)J.K- =-8.924J.K-
因是絕熱可逆過程,△S=△Sx+△SB=0,故有△SB=-△SA=8.924J·K
或
AS(B)=C(B)-Rin=(6xRx 6837-6xR*
=8.924J·K-
3-18 單原子氣體 A 與雙原子氣體 B 的理想氣體化合物共 8 mol,組成為 y(B)= 0.25,始態 T: = 400 K,V: = 50 dm'.今絕熱反抗某恒定外壓不可逆膨脹至末態體積 V: = 250 dm3的平衡態..求過程的W, △U, △H, AS.
解:先求混合物的摩爾定壓熱容
Cv=ygCp(B)=0.25×R+0.75xR=1.75R
Q=0,W=△U
-Pumb(V2-V1)=nCy.m.mix (T2-T1)
nET(V2-V)=nx1.75R(T2-T1)
√
將數據代入,得2.55T:=1.75T=1.75×400K,故T=274.51K
W=AU=(8×1.75R×(274.51-400)]J=-14610J=-14.61kJ
Cp.m.mix =Cv.m.mix +R=1.75R+R=2.75R
△H={8×2.75R×(274.51-400)}J=-22954.J=-22.95kJ
nB = yBn =0.25 × 8mol =2mol, nA = 6mol
AS(A)=nACm(A)In+nARIn
={6xRxn+6×RIn
]J.K=(-28.172+80.29]J.K=52.118J.KAS(B)=nCpm(B)In+nBRlnV
=(2xRIn27451+2xRIn250)J.K=(-15.651+26.763)J-K=11.112JKAS=AS(A)+AS(B)=(52.118+11.112)JK=63.23.J.K
3-19常壓下將100g,27C的水與200g,72℃的水在絕熱容器中混合,求最終溫
度t及過程的△S.已知水的比定壓熱容cp=4.184J·g·K.
解:Q=0,△H=0,△H1+△H=0
100×4.184×(T:-300.15K)+200×4.184×(T:-345.15K)=0
T:-300.15K+2×(T:-345.15K)=0
T:=330.15K即t=57℃
AS={100×4.184×In330.15330.15
+200×4.184×lnJ.K-1=2.68 J.K
300.15345.15
3-20將溫度均為300K,壓力為100kPa的100dm的H:(g)與50dm的CH(g)
恒溫恒壓混合,求過程的△S.假設H:(g)和CH(g)均可認為是理想氣體。
解:an=100x10x50x10]mol=16.67mol
"=(100x10'x100x10mol=3mo
ASASASC RInn RIn
=33.333×8.3145×ln150+16.667×8.3145×ln150
50
=(13.516+18.310)J·K=31.83J·K
3-21絕熱恒容容器中有一絕熱隔板,隔板一側為2mo1的200K,50dm的單原子理
想氣體A,另一側為3mol的400K,100dm2的雙原子理想氣體B。今將容器中絕熱隔板抽
去,氣體A與氣體B混合達到平衡態。求過程的△S
解:Q=0,W=0,△U=0,則有△U(單)+△U(雙)=0
2xR×(T2-200K)+3xR×(T2-400K)=0
解得T:=342.86K
△S(A)=nC(B)ln2+nn{2Rxln342.86
200+2x Rxin K
=31.714J·K
)-C,7 i r na s m o d
=0.502 JK
△S=△S(A)+△S(B)=(31.714+0.502)J·K=32.216 J·K=32.22 J·K
3-22絕熱容器恒容容器中有一絕熱隔板,隔板兩側均為N:(g)。一側容積為50dm3,
內有200K的N:(g)2mo1;另一側容積為75dm3,內有500K的N:(g)4mo1。今將容器中
絕熱隔板抽去,使系統達到平衡態。求過程的△S
解:設左側的N:(g)用A代表,左側的N:(g)用B代表。混合過程示意如下:A,2molB,4mol
△SA
2 molA
B,4mol
50dm',75dm3,
VA,
V,
200K,pA500K,p
△S
T;p
T;p
Q=0,W=0,△U=0,則有△U(A)+△U(B)=0
2×Cv×(T2-200K)+4×C×(T2-500K)=0解得T:=400K
方法一:若用分體積計算熵變:
V=(2/6)×125dm3=41.67dm3, V =(4/6)×125dm3=83.33dm3,
A(A)-m.(B)1 I 2x xin goo41.67
+2xRxIn
=(28.816-3.030)J.K=25.786J.K
AS(B)=nC(B)ln+nRln4n4008333
+4xR×InJ.K-
50075
=(-18.553+3.503)=-15.05.JK
△S=△S(A)+△S(B)=(24.786-15.05)JK'=10.736J·K
方法二:先計算A和B各自初始壓力及終態壓力
2×8.315×2004×8.315×500
PA=-=66.52kPa: P=
=221.73kPa
50×10375×103
6×8.315×400
p=-=159.65kPa
125×10
)-C(T RI x xn g oo
40066.52
+2xRxInJ.K-
159.65
=(40.345-14.559)J-K=25.786J.K
AS(B)=(B)in T narin ax Rxin goo
40(221.73
+4×RxInJ.K-
159.65
=(-25.976+10.925)J.K=15.05J-K
△S=△S(A)+△S(B)=(24.786-15.05)J·K=10.736J·K
3-23甲醇(CH0H)在101.325kPa下的點(正常沸點)為64.65℃,在此條件下的
摩爾蒸發焓△H=35.32kJ·mol。求在上述溫度、壓力條件下,1kg液態甲醇全部變
成甲醇蒸氣時的Q,W,△U,△H及△S
解:n=(1000÷32)mo1=31.25mol
Q=Q=△H=n△H=(31.25×35.32) kJ=1103.75 kJ
W=-(V-V.)-poaV.-n RT
=(-31.25×8.3145×337.80}=-87770J=-87.77 kJ
△U=Q-W=(1103.75-87.77)kJ=1015.98 kJ
△S = n△Hm / T = (1103750÷337.80) = 3267 J.K'=3.267 k J·K
3-24常壓下冰的熔點為0℃,比熔化h=333.3J·g,水比定壓熱容c=4.184
J·g·K。在一絕熱容器中有1kg,25℃的水,現向容器中加入0.5kg,0℃的冰,這是系
統的始態。求系統達到平衡態后,過程的△S
解:常壓絕熱混合,Q=0,設末態溫度為T:(T:>273.15K),于是有
500×333.3+500×4.184×(T:-273.15K)+1000×4.184×(T:-298315K)=0解得T2=263K
顯然,-10℃這個結果不合理。因此,只是高溫水放出熱量使部分冰熔化,溫度仍是0℃
設0℃冰量為m,則0℃水量為(500-m)g,其狀態示意如下
500g, H2O(s), 273.15K 0(500-m)gH2O(l), mH2O(s), 273.15K
1000g, H2O(1), 298.15K1000g, H2O(1), 273.15K
(500-m)g×333.3J·g'+1000g×4.184 J.gK'× (273.15K-298.15K)=0
333.3m=62050g
m=186.17 g0℃熔化的水量=(500-186.17)g=313.83g
AS=AS(H2O, s)+AS(H2O,I)
313.83×333.3273.15
+1000×4.184×InJ.K=16.52J.K
273.15298.15
3-25常壓下冰的熔點為0℃,比熔化焓△mh=33.3J·g,水比定壓熱容c2=4.184
J·g·K。若系統的始態為一絕熱容器中有1kg,80℃的水及0.5kg,0℃的冰。求系統達
到平衡態后,過程的△S.
解:常壓絕熱混合,Q=0,
500g× 333.3J·g+500×4.184 J.g.K'×(T-273.15K)
+1000g ×4.184 Jg K'×(T-353.15K)=0
12.552T=3764.7188KT=299.93K
冰的熵變:
△S1=△S(H2O,s)+△S(H2O,l)
500×333.3299.93
+500×4.184×InJ.K=805.765.J.K
27315273.15
水的熵變:AS2=(1000×4.184×1n299.3J.K=-683.430JK
3531
△S=AS1+△S=122.33 JK
3-26常壓下冰的熔點為0℃,比熔化焓△mh=333.3J·g,水和冰的比定壓熱容
c(H0,1)=4.184 J·g·K'及c(H0,s)=2.000J·g·K'。若系統的始態為一
絕熱容器中有1kg,25℃的水及0.5kg,-10℃的冰。求系統達到平衡態后,過程的△S.
解:和3-24題類似,高溫水放出熱量使部分冰熔化,溫度仍是0℃。設0℃冰量為m,
則0℃水量為(500-m)g,其狀態示意如下
500g, H2O(s), 263.15K=0(500-m)gH2O(), mH2O(s), 273.15K
1000g,H,O(1), 298.15K1000g, H2O(1),273.15K
500×2.00Jg·K×(273.15K-263.15K)+(500-m)g×333.3J·g
+1000g ×4.184 J.gK×(273.15K-298.15K)=0
333.3m=72050g
m=216.17g熔化的水量=(500-216.17)g=283.83g
冰的熵變:
AS1=AS(H2O. S)+AS(H2O,s)
=500×2x1n273.15283.83×333.3+J.K=383.63J-K
263.15273.15
水的熵變:AS2=(1000×4.184×In735JK=-366.42JK
△S=△S1+△S:=17.21J.K
3-27已知下冰的熔點為0℃,摩爾熔化焓△rH(H0)=6.004kJ·mo1,苯的熔點
為5.51C,摩爾熔化焓△H(CH)=9.832kJ·mo1。液態水和固態苯的定壓摩爾熱容
C(H0, 1)=75.37 J·mol·K'及C(CH,s) =122.59 J· mol· K'.今有兩個用絕熱層包圍的容器,一容器中為0C的8molH0(s)與2mo1H0(1)成
平衡。另一容器中為5.51℃的5mo1CH(1)與5molCH(s)成平衡。
現將兩容器接觸,去掉兩容器間的絕熱層,使兩容器達到新的平衡。求過程的△S。
解:設液態苯全部凝固,冰全部融化,于是示意如下
8molH2O(s), 2molH2O(1), 0C 8molH2O(1), 2molH2O(1), t
5molCH(s), 5molCH (1).5.51°C5molCH (s), 5molCH(s),t
8mol×6004J·mol'+10mol×75.37J· mol.K(T2-273.15K)
+5mol×(-9832)J·mol'+10mol×122.59J· mol.K×(T2-278.66K)=01979.6T2=548610.395KT2=277.13K
所以,t=3.98℃,0℃<3.98℃<5.51℃,假設合理。
AS(H:O)=
10×75371n8*
=(175.845+11.392)J·K=187.24J·K
AS(C6H)=+10×122.59n.K
27866
=(-176.416-5.953)J·K=-182.37J·K
△S=△S1+ △S2= 187.24J·K-182.37J·K=4.87J·K
3-28將裝有0.1mo1乙醚(CH):0(1)的微小玻璃放入的小玻璃瓶放入容積為10dm3的恒
容密閉的真空容器中,并在35.51℃的恒溫槽中恒溫。35.51℃為在101.325kPa下乙醚的沸
點。已知在此條件下乙醚的摩爾蒸發焓△Hm=25.104kJ·mol。今將小瓶打破,乙醚蒸發
至平衡態。求:(1)乙醚蒸氣的壓力;(2)過程的Q,△U,△H及△S。
解:(1)P乙.=nRT/V=(0.1×8.314×308.66/10)kPa=25.664kPa
(3)畫出如下框圖:
0.1mol乙醚(1)AH
AS0.1mol乙醚(g)
35.51C, p=0kPa35.51C.25.664kPa
△H↓△S
0.1mol乙醚(1)△H2
△S2
35.51C,101.325kPa
△H↓△S:
0.1mol乙醚(g)
35.51C,101.325kPa
AH≈0: AS≈0: AH1≈0.1×25.104kJ=2.5104kJ△H2≈0
△H=△H1+△H =2.5104kJ; W=0; Q=△U=△H-△(pV)≈△H-nRT=2.2538kJAS =AH /T=(2.5104×103/308.66).J.K=8.133J.K
AS2=nRIn(p1/p2)=[0.1×8.3141n(101.325/25.664)]J.K=1.142J.K△S=△S+△S:=9.275JK
3-29已知苯(CH)在101.325kPa下于80.1C,△Hm=30.878kJ·mo1。液
體苯的摩爾定壓熱容C。。=142.7J·mo1·K
今將40.53Kpa,80.1℃的苯蒸氣1mo1,先恒溫可逆壓縮至101.325kPa,并凝結成
液態苯,再在恒壓下將其冷卻至60℃。求整個過程的Q,W,△U,△H及△S。
解:把苯蒸氣看作是理想氣體,恒溫可逆壓縮時,△U:=0,△H=0,于是有
W=nRT In(p/p1)={1×8.3145×353.25×ln(101.325/40.53)]J=2691J
W2=-Pamb (V1-Vg)≈pambVg=ngRT= (1X8.3145×353.25)J=2937.1J
W3≈0: W=W+W2+W3=(2691+2937.1+0)J=5628J=5.628kJ
△U1=0,Q1=W1=2937J: Q2=-30878J
Q3=[nCdT=1×14.27×(333.15-353.25)]J=-2868J
Q=Q1+Q2+Q3={(-2691)+(-30878)+(-2868)=-36437J=-36.437kJ
△U=Q+W=-36.437 kJ+5.628 kJ=-30.809 kJ
△H=△H1+△H2+ △H3={0+(-30.868)+(-2.868)}kJ=-33.746 kJ
3-30容積為20dm的密閉容器中共有2mo1H0成氣液兩相平衡。已知80℃,100℃
下水的飽和蒸氣壓分別為p:=47.343kPa及p=101.325kPa,25℃水的摩爾蒸發焓△H=
44.106kJ·mol';水和蒸氣在25-100℃間的平均摩爾定壓熱容Cm(H0,1)=75.75
J·mol·K和Cpm(H0,g)=33.76J·mol·K3今將系統從80℃的平衡態加熱到100℃
的平衡態。求過程的Q,△U,△H及△S。
解:因液態水占的體積小,可以認為20dm3的密閉容器體積是氣體的體積,于是,與
液態成平衡的水氣的物質的量為
始態:P.V
ng.353.15KRT,47.343×103×20×10
8.314×353.15mol = 0.3225mol
末態:ng.373.15KV101.325x10x20x103
mol =0.6532mol
8.314×373.15
始態液態水的物質的量 = 2mol - 0.325 mol =1.6675 mol
末態液態水的物質的量 = 2mol - 0.6532 mol =1.3468 mol
為求過程的Q,△U,△H及△S,設計如下途徑:
1.6775mol H,O(1)1.3468mol H20(1)
0.3225 mol H20(g)0.6532 mol H20(g)
353.15K,20 dm3373.15K,20 dm3
ΔΗΔΗ4
1.6775molH20(1)1.3468mol H20(1)
0.3225 mol H20(g)→0.6532 mol H20(g)
298.15K298.15K
ΔΗ=(1.6775×75.75× (298.15-353.15) +0.3225×33.76× (298.15-353.15) )J
(-6988.88-598.82 ) =-7587.7J
ΔΗ2={ (1.6775-1.3468 ) ×44106)J= 14556.1J
ΔΗ3= (1.3468×75.75× (373.15.15-298.15) +0.6532×33.76× (373.15-298.15) )JΔΗ= ΔΗ, + ΔΗ2 + ΔΗ3 =16274 J =16.274 kJ
ΔU= ΔΗ+ Δ (pV) =ΔΗ+VΔp
= (7651.5 + 1653.9 ) = 9305.4J
={ 16274 + 20×10× (101.325-47.343) ×103J = 15195 J= 15.20 kJ
因密閉恒容,W=0,Q= △U=15.20 kJ
298.15298.15
353.15
+0.3225×33.76×In
353.15
△S, =1.6775×75.75×InJ·K
AS2(-21.513-1.843) J·K=-23.356J·K
(1.6775-1.3468)×44106J.K- = 48.921J.K-1
AS31.3468×75.75×InJ-K-
(22.892 +4.948 )J·K = 27.840J·K
AS= △S+ △S2+ △S3=53.405J·K
298.15373.15373.15
+0.6532×33.76×In
298.15298.15
3-31 0z(g)的摩爾定壓熱容與溫度的函數關系為
C=(28.17+6.297x10(TIK)-0.7494x10(T/K))J.mol-.K-1
已知 25℃T 0:(g) 的標準摩爾熵 s°=205.138J-mol--K-1.求 0z(g)在 100℃,50 kPa
下的摩爾規定熵值 S.
解: ds=T.d=
將 0:(g)的摩爾定壓熱容與溫度的函數關系代入上式積分,整理得s°(T)=S(298.15K)+(28.17xIn 20815x+6.297x10(T-298.15K)
-x0.7494x10-°[(TIK)'-(298.15K/K)}-mot--K-1
S(373.15K)=(205.138+6.3209+0.4723-9.5377)J-K-=202.394J-K-1
這是標準摩爾熵。為求氧氣在 100℃,50 kPa 下的摩爾規定熵值 S.,設計如下途徑:
Imol O,(g)1mol O2(g)
373.15K,p°=100kPa→373.15K,p=50kPa
S°(373.15K)S(373.15K)
AS =-nR In(p2/ p)=S-S2
Sm = S° + AS = S° -nR In(p2/ pi)
= (202.394-1x8.3145xin 50.K = 208.157J-K
假如忽略三次方項,則
S(373.15K)= (205.138+6.3209+0.4723)J·K-=211.932J-K-
S= S° + AS = S° - nR In(p2 / p,)結果與答案一樣。
= (211.932-1x8.3145xim 0).217.695 = ?J.K-1
3-32 若參加化學反應各物質的摩爾定壓熱容可表示成 C=a+bT+cT2. 試推導化
學反應0=2v,B的標準摩爾反應熵△.S°(7)與溫度T的函數關系式,并說明積分常數
△,So如何確定
解:對于化學反應0=ΣvBdA,S I dT = ACIT
(3.6.7b)
在溫度區間Tr至T2內,若所有反應物及產物均不發生相變化,反應物和產物的標準定壓摩
爾熱容隨溫度的關系式均為C=a+bT +cT2
令Δα= Σν, Δb= Σνb, Δe = Σν,則有
Δ,C = Δa + ΔbT + ΔcT
代入式子(3.6.7b),則可得不定積分式
Δ.S(T) =A,S + ΔaInT +ΔbT+ΔcT
式中△,S%.0為積分常數,將某一溫度下的標準摩爾反應熵代入即可求得。
3-33 已知 25℃ 時液態水的標準摩爾生成吉布斯函數 △,G(H,O,1)=-237.129
kJ·mo1”。水在 25℃ 時的飽和蒸氣壓 p°=3.1663 kPa.求 25℃時水蒸氣的標準摩爾生成吉
布斯函數。
解:過程為Imol H,O(1)1mol H20(g)
298.15K, p° =100kPa ΔG 298.15K, p=100kPa
Δ,G(H2O(1),298.15K)Δ,G(H2O(g),298.15K)
AG△G3
1mol H20(1)
298.15K, p=3.1663kPaImol H2O(g)
298.15K, p= 3.1663kPa
ΔG= ΔG, +ΔG, +ΔG, =Δ,G(H,O,g,298.15K)-Δ,G(H,O,1,298.15K)
△Gj=Vi△p={ (18÷1000) ×103× (3.1663-100) ×103}J=-1.743J;△G2 =0;
△G= Vdp = nRT In(p2/p)
=(1×8.3145×298.15×In (100/3.1663) J= 8558.9J=8.559 kJ
Δ,G(H,O, g,298.15K)=ΔG, +ΔG, +ΔG, +Δ,G(Η,O,1,298.15K)
(-0.0017+8.559 - 237.129) kJ ·mol-=-228.572 kJ· mo1"
3-34 100℃的恒溫槽中有一帶活塞的導熱圓筒,筒中為 2 mol Nz(g)及裝于小玻璃瓶
中的 3 mol H0 (1). 環境的壓力即系統的壓力維持 120 kPa 不變.
今小玻璃瓶打碎,液態水蒸發至平衡態.求過程的Q, W, △U, △H, △S, △A及△G.
已知:水在 100℃時的飽和蒸氣壓為 p'=101.325kPa,在此條件下水的摩爾蒸發焓 △…,H
40.668 kJ·mol.
解:見書本例 3.5.2(p122)。本題雖然系統的壓力為 120kPa,大于水在 100℃時的飽
和蒸氣壓,但因有N: (g)存在,在氣相中水蒸氣的分壓小于其飽和蒸氣壓時,水即可蒸發。
本題的水量較多,水是全部蒸發,還是部分蒸發,我們先計算為好。
先求水的蒸發量。水在 100℃時的飽和蒸氣壓為 p'=101.325kPa,末態 N:(g) 的分壓 p:
(N,g)=p -p(H20)=18.675 kPa.N(g)的物質的量為 2mol,據分壓定律,求得水
蒸氣的物質的量為
n(H,0,g)=[p(H,0,g)/ p(N,)]×n(N,)=(101.325/18.675)×2mol =5.426mol
可見,3mol 的水全部蒸發成水蒸氣。
B ΔΗ (N2, g) =0, ΔΗ (H20, g) =3x Δ.,H=3 x 40. 668kJ =122.004 kJΔΗ =122.004kJ =Q,
W=-p△V=-{An (g) RT)=-n (H;0, g) RT={-3×8.3145×373.15)J=-9.308 kJ
ΔU = Q + W = 122.004 kJ - 9.308 kJ = 112.696 kJ
ΔS(H20) = ΔΗ IT = (122.004×103 /373.15)J-K-1 =326.957J-K-1
AS(N2)= n2RIn(P.x, I P2.N,)=[2x8.314In(120/18.675)J-K- =30.933J-K-AS= AS (H20) + AS (N2) =357.89 J.K
ΔΑ = ΔU - TΔS = 112696J-373.15×357.89 J =-20850J =- 20.850 kJΔG = ΔΗ - TAS = 122004J-373.15×357.89 J=-11543 J=- 11.543 kJ3-35 已知 100℃水的飽和蒸氣壓為 101.325kPa,在此條件下水的摩爾蒸發焓 △,H
40.668 kJ·mol".在置于 100℃恒溫槽中的容積為 100 dm’的密閉容器中,有壓力 120kPa
的過飽和蒸氣。此狀態為亞穩態。今過飽和蒸氣失穩,部分凝結成液態水達到熱力學穩定的
平衡態。求過程的Q, △U, △H, △S, △A及△G.
解:先計算容積為 100 dm'的密閉容器中水蒸氣的物質的量:
始態:n=PV120×10'×100×10
8.3145×373.15mol = 3.8680mol
末態:n=P101.325×10'×100×10
8.3145×373.15mol = 3.2659mol
可設計如下過程
3.8680mol H,O(g)
120kPa, 100dm',373.15KA3.2659mol H2O(g), 0.6021mol H20(1)
101.325kPa. 100dm.373.15K
ΔΗΔΗ,
3.8680mol H,O(g)3.2659mol H2O(g), 0.6021mol H20(1)
101.325kPa,373.15K101.325kPa, 373.15K
ΔΗ=ΔΗ,=0 ΔΗ=ΔΗ, =0.6021x (-40.668) kJ= - 24.486 kJ
△U= ΔΗ-Δ(pV) ~ΔH- {An (g) RT)
=(- 24.486 - (-0.6121) × 8. 3145 × 373. 15 × 10) kJ =-22.618 kJ
恒容, W=0; AU = Q = - 22.618 kJ
ΔS = (-3.868×8.3145×In(101.325/120)-24486/373.15)J.K-
=(5.440 - 65.62)J·K =- 60.180 J·K
ΔΑ = ΔU - TΔS = {-22618-373.15× (-60.180) }J=-162J =-0.162 kJΔG = ΔΗ - TAS = {-24486-373.15× (-60.180) }J =-2030 J =-2.030 kJ3-36 已知在 101.325 kPa 下,水的沸點為 100℃,其比蒸發焓 △…h=2257.4 kJ·kg'。
已知液態水和水蒸氣在 100~120℃范圍內的平均比定壓熱容分別為 cp(H2O,1)=4.224
kJ·kg·K'及 cp(H20,g)= 2.033 kJ·kg·K".
今有 101. 325kPa 下 120℃的 1 kg 過熱水變成同樣溫度、壓力下的水蒸氣。設計可逆
過程,并按可逆途徑分別求過程的 △S 及 △G.
解:途徑設計如下1kgH20(1)
393.15K,101.325kPalkgH20(g)
393.15K,101.325kPa
ASAS2
1kgH20(1)1kgH20(g)
373.15K,101.325kPa373.15K,101.325kPa
373.15 2257.4393.15
AS= AS, +AS2 +ΔS,= 1x4.244xIn+1×2.033xIn
393.15373.15373.15
kJ·K-
= (-221.582 + 6049.578 + 106.144) J? K'= 5934J? K
ΔΗ, = m sCdT =1x4244x (373.15-393.15) = -84880
ΔΗ2 = 2257400 JΔΗ, =[1x 2033x (393.15-373.15) = 40660J
ΔΗ = ΔΗ, + ΔΗ2 + ΔΗ,= 2213180J
ΔG=ΔΗ-TAS=2213180- 393.15×5934 ) J=-119772 J=-119.772 kJ
3-37 已知在 100kPa 下水的凝固點為 0 ℃, 在 -5℃,過冷水的比凝固焓 △h=-322.4J·g',過冷水和冰的飽和蒸氣壓分別為 p'(H,O,/)=0.422 kPa,p'(H,O,s)=0.414 kPa.今在 100 kPa 下,有 -5℃ 1kg 的過冷水變成同樣溫度、同樣壓力下的冰,設計可逆途徑,分別按可逆途徑計算過程的 △S 及 △G.
解:途徑設計如下1kgH20(1)1kgH20(s)
268.15.15K,100kPa268.15K,100kPa
AS△Ss
1kgH,O(1)
268.15.15K,0.422kPaIkgH,O(s)
268.15K,0.414kPa
△S△S
lkgH20(g)
268.15.15K,0.422kPalkgH20(g)
268.15K,0.414kPa
△S,≈0, △Ss≈0,
△S2+△S=Δ化H-ΔηφH_-Δ熔化H_ΔH
268.15K268.15K 268.15K 268.15K
1000x(-322.4)]J·K=-1202.312J·K
268.15
AS=RTInP10000.422
×8.3145 In0.414J.K=8.840J·K
所以,△S= △S2+△S++△S3=-1193.5J·K-'=1.194kJ·K
又因 △G2=0, △G4=0, △G≈ 0, △Gs≈0,
△G= △G, =nRT In P=1000
p.18×8.314×268.15×In 0.4147
0.422J =-2370J =-2.370kJ
3-38 已知在 -5℃,水和冰的密度分別為 p(H,0,/)=999.2 kg·m’和 p(H,O,s)=916.7kg·m’。在在 -5℃,水和冰的相平衡壓力為 59.8 Mpa。
今有-5℃的 1kg 水在 100kPa 下凝固成同樣溫度、壓力下的冰,求過程的△G。假設水和冰的密度不隨壓力改變。
解:途徑設計如下1kgH20(1)AS
268.15.15K,100kPa1kgH20(s)
268.15K,100kPa
△G,△G
lkgH20(1)AG
268.15.15K,59.80MPalkgH2O(s)
268.15K,59.80MPa
因相平衡,△G2=0Α
△G= △G, +△G, =Jo0LPaV dp+V.dp
P
A00tP (Vx-Vx) dp=(Vx-Vx)x(100-59800)x10'Pa
x(100-59800)x10 J=-5377J =-5.377kJ
98MP
916.7 999.2
3-39 若在某溫度范圍內,一液體及其蒸氣的摩爾定壓熱容均可表示成
C=a +bT +cT2
的形式,則液體的摩爾蒸發焓為AH. = ΔH + ΔaT +ΔbT +T
其中△a=a(g)-a(1),△b=b(g)-b(1),△c=c(g)-c(1),△Ho為積分常數.試用克勞修斯-克拉佩龍方程的微分式,推導出該溫度范圍內液體飽和蒸氣壓 p 的對數
Inp 與熱力學溫度 T 的函數關系式,積分常數為 I.
解:推導如下:
dinp-1
對上式作不定積分得
Inp=-AH+T+T+T+1
CH,(g)+CO2(g)=2CO(g)+2H2(g)
3-40 化學反應如下:
(1) 利用附錄中各物質的 s°,△,H°數據,求上述反應在 25℃時的△,S°,△,G°:(2)利用附錄中各物質的 △,G°數據,計算上述反應在 25℃時的 △,G°:
(3)25℃,若始態CH.(g)和CO2(g)的分壓均為 150kPa,末態 CO(g)和 H2(g)的分壓
均為 50kPa,求反應的 △,S,△,G。
解:列表如下
物質ΔΗ/kJ ? mol
Δ,G/kJ ? mol
S/J·mol'·K
H2(g)0
CO(g)-110.525
0
-137.168130.684
197.674
CH↓(g)-74.81
-50.72
186.264
CO2(g)-393.509
-394.359
213.74
(1) A,S=vS=(2×130.684+2×197.674-186.264-213.74) J· mol1·K
=256.712 J molK
△,H=∑vgA,H=[2×0+2×(-110.525)-(-393.509)-(-74.81)}kJ·mol'
=247.269 kJ·mol
A,G =A, H -TA,S= {247269-298.15×256.712}= 170730 J mol'= 170.730 kJ mol'
(2) Δ,G=∑vgA,G={2×0+2× (-137.168) -(-394.359) -(-50.72)}kJ· mol'
=170.743 kJ·mol
(3)設計如下途徑
CH4(g,100kPa)+CO(g.100kPa)→2CO(g,100kPa)+2H(g.100kPa)
△G△G2
CH4(g,l50kPa)+CO(g.150kPa)-.=→2CO(g,50kPa)+2H(g.50kPa)
AG1 = n(CH4)× RT In(150/100)+ n(CO2)RT In(150/100)=2RT In(150/100)
=2010.27 J·mol
AG2 =4RT In(100/50)=6873.16 J· mol
A,G=A,G-AG1 -AG2=(170743-2010-6873)kJ· mol
=161860Jmol=161.860kJmol
AS=AS-AS1-AS2 =AS+2RIn(150/100)-4R In(50/100)
={256.712+6.742+23.053J· mol·K=286.507J· molK
3-41已知化應0=vB中物的摩定壓熱容與溫度間的關為
BCpm=a+bT+cT2
則該反應的標準摩爾反應熵與溫度的關系為
△,S(T)=△,S+AalnT+△bT+△cT
(見習題3-32).試用熱力學基本方程dG=-SdT+Vdp推導出該化學反應的標準摩爾反應吉
布斯函數G(T)與溫度T的函數關系式。說明積分常數.G如何確定。
解:dG=-SdT+Vdp,恒壓下,dG=-SdT
因該化學反應始終在恒壓p下進行,上式可寫成
d△,G(T)=-A,S(T)dT=-[A,S+AalnT+AbT+AcT)dT(a)
對式(a)進行不定積分,得
△,G(T)=A,G-AaTlnT-T2-AcT2-A,ST式中積分常數△.G。
即可用該
化學反應的某個溫度的A.G°(T)及A.S°代入上式求得
3-42Hg在100kPa下的熔點為-38.87℃,此時比熔化Ah=9.75J·g;液
態汞和固態汞的密度分別為p()=13.690g·cm3和p(s)=14.193g·cm3求:
(1)壓力為10Mpa下的熔點;(2)若要汞的熔點為-35℃,壓力需增大多少。
解:(1)壓力為10Mpa下的熔點:
已知PI-P1AV in
P2-P19.75
=3.7663×10n
In
Pa Pa×10
T
13.69014.193
10000×10-100×10=3.7663×101n(T/234.28K)
InT=[(10000-100)×10'÷(3.7663×10)]+1n234.28K
T2=234.89Kt=-38.26℃
(2)若要汞的熔點為-35℃,需增大的壓力計算如下
P2_P19.75
PaPa×10
n=3.7663×101n
T
13.69014.193
p-100×10Pa=3.7663×10'1n(238.15/234.28K)Pa
p=[3.7663×101n(238.15/234.28K)+100×10]Pa
p=(61706102+100×103)Pa=61806102 Pa=61.80MPa
3-43已知水在77℃時的飽和蒸氣壓為48.891kPa。水在101.325kPa下的正常點
為100℃。求
(1)下面表示水的蒸氣壓與溫度關系的方程式中A和B值;
lg(p/Pa)=-A/T+B
(2)在此溫度范圍內水的摩爾蒸發焓;
(3)在多大壓力下水的沸點為105℃。
解:(1)求常數A和B
lg 48891=-A/350.15K+B(a)
lg101325=-A/373.15K+B(b)
式(a)和式(b)聯立求解得A=2179.133K,B=10.84555
(2)A=AH(2.303R)
AH=2.303RA=2.303×8.314×2179.1333J.mol=41.719kJ.mol(3)1g(p/Pa)=(-2179.133/378.15)+10.84555
所以有p=121.042kPa
3-4水(H20)和氯仿(CHC13)在101.325kPa下的正常沸點分別為100°℃和61.5℃,摩爾蒸發焓分別為A_H_(HO)=40.668kJ·mol'和A_H_(CHC)=29.50kJ·mol'。求兩液體具有相同飽和蒸氣壓時的溫度。
解:由式()
P
可得40.668×10
29.50×10
In101325PaR
373.15K
R
334.65KT
40.668-29.50
T=K=536.05K
40.668/373.15-29.50/334.65
t=262.9℃
3-45一溫度下液體及其飽和蒸氣壓的摩定壓熱容Cm(1),C(),液體的摩爾蒸發焓是溫度的函數:
ApHm=△H+{CPm(g)-Cpm(l)T
試推導液體飽和蒸氣壓與溫度關系的克勞修斯-克拉佩龍方程的不定積分式。
解:克勞修斯-克拉佩龍方程的微分式為
din p m ar-AMo +((8)-Cm
dT
RTE
am e .R F O o
對上式作不定積分,得
AHC .m(g)-C .m(1)
np=--InT+C
rTR
積分常數C用已知液體的某一溫度T及其飽和蒸氣壓p來代入上式即可求得
3-46:(1)dH+-()}
(2)對理想氣體(=0
解:(1)證明如下
H=H(T,p)
dn )e p)d)(a)
an s o
-9)ar
所以)(b)
引用麥克斯韋關系式--代入上式,得
()-v-r()(c)
將式(c)代入式(a)得on-c,y)
(2)對理想氣體
)=v-r()=v-r[&(m/D]=v-m-v-v=03-47求證:(1)=(P-a,TW:(2)對理想氣體=0-
式中為體膨脹系數,
x=()為等溫壓縮率
提示:從U=H-pV出發,可應用習題3-46的結果
解:(1)本題采用另一方法求證如下:
a -70)o or
--p(a )a )dp
所以()())
引用麥克斯韋關系式(#),)代入上式,得
(()
{()()}=(pKT-Tay)V
(2)對理想氣體
()()
[][nRTnRT
H
0
PP
3-48求證:
(1)ds)(av:
(2)對理想氣體dS=Cdlnp+CdlnV.
證:(1)S=S(p,V)
ds=(s p)dp+(s1v)dV
=(S 1T) (T 1p) dp+(S1T), (T 1oV), dV
oTdV
H
d+)v=-+-()v
(1)對于理想氣體T=pV/(nR)
as t=+c,dinv
TnR
3-49求證:
(1)as)
(2)對范德華氣體,且C為定值,絕熱可逆過程方程式為
T(Vm-b)=定值
p+)n-b)y2=定值
提示:絕熱可逆過程△S=0
解:(1)求證如下
S=S(T,V)
as-()ar()av)av
引用麥克斯韋關系式將上式整理得
as)
(2)對范德華氣體,絕熱可逆過程:dS=0,由(1)得
()()(a)
范德華方程為.
-b)=RT,故有
(,-evor-Rnw.
代入式(a)得Cp.m
(V -b)
arT
R
RdVCom
d
(V-b)
不定積分上式
RIn(V-b)=-CInT+InCRIn(V-b)+CInT= InCIn(V-b)T-=In C
所以有TCr-(V-b)=C=定值
(b)
而范德華方程為(+)
,-b)=RT,將T定值
代入范德華方程得
(V.-by4
(n+)(-b)
(+)
(V-6)-=R×定值=定值
所以有()
V -b)Gi tR=定值證畢。
3-50證明:(1)焦耳-湯姆遜系數()
(2)對理想氣體1-=0。
解(1)證明如下:
dH=TdS+Vdp(a ap
+()]+v
引用麥克斯韋關系式()()
n-[r-()]+v.=c,r+[(),+v.]因節流膨脹為恒焓過程,dH=0,上式整理變成
(()}
(2)對于理想氣體
r()v-[]-v-v-v-0
故v-v}=0=μ
證畢。
第四章多組分系統熱力學
4-1由溶劑A與溶質B形成一定組成的溶液。此溶液中B的濃度為c,質量摩爾濃度為b,此溶液的密度為p。以M,M分別代表溶劑和溶質的摩爾質量,若溶液的組成用B的摩爾分數X表示時,試導出X與c,x與b之間的關系式
解:對于A,B二組分溶液,溶液中物質B的物質的量n與溶液的物質的量之比,稱為物質B的摩爾分數,符號xB即XB
+n
物質B的物質的量濃度為cB在二組分溶液中,溶質B的摩爾分數x與其濃
溶液
度c之間的關系為
溶液CH
CB
CB
CB
+nnA
mAIM
(m-m)
(m-mn)/V
CBX溶液V
溶液MAV
溶液MA
CBCB
(P-RM/V)(P-CM
CH+
B
MAMA
式中p為溶液的密度,單位為kgm3;A代表溶劑
而物質B的質量摩爾濃度則是溶液中溶質B的物質的量除以溶劑的質量即
bB”
mA
其單位為mol·kg。在二組分溶液中溶質B的摩爾分數x與質量摩爾濃度b的關系為
bs
nB/mA+nAmA bB+nA /(nAMA) bB+1/M
4-2D-果糖CH:0(B)溶于水(A)中形成的某溶液,質量分數W=0.095,此溶液在20℃時的密度p=1.0365Mg·m3。求此果糖溶液的(1)摩爾分數;(2)濃度;(3)質量摩爾濃度。
解:(1)W/M.
0.095/180
B=0.0104
WBIM+(1-W)/MB 0.095/180+0.905/18
(2)CB0.095/180x103mol.dm3=0.547mol.dm
1/1.0365
(3)bB0.095/180
x103mol-kg=0.583mol.kg
(1-0.095)/1000
4-3在25℃、1kg水(A)溶解有醋酸(B),當醋酸的質量摩爾濃度b介于0.16和2.5mo1·kg之間時,溶液的總體積V/cm=1002.935+51.832×(ba/mo1·kg)+0.1394(ba/mol·kg)。(1)把水(A)和醋酸的偏摩爾體積分別表示成ba的函數關系式;(2)求b=1.5mol·kg時水和醋酸的偏摩爾體積。
解:(1)VB=(V10nB)T.pen =(V1bB)T.pnA=5.5mo
=(51.832+0.2788 ba/ mo1 kg cm' mol
1000
V=VBnB+VAnA=VBbBkg+VAmol
18.015
VV-Vb/kg1002.935-0.1394(b/ mol.kg)cm3. mol
55.5mol55.5
=(18.0681-0.0025(ba/ mo1kg')3}cm3mo1
(2)V=(18.0681-0.0025×0.152)cm.mo1'=18.0625 cmmolV=(51.832+0.2788×0.15) cm'. mo1'=52.25 cm'. mo1'
4-460℃時甲醇的飽和蒸氣壓是83.4kPa,乙醇的飽和蒸氣壓是47.0kPa.二者可形成
理想液態混合物,若混合物的組成為質量百分數各50%,求60℃時此混合物的平衡蒸氣組成,
以摩爾分數表示。
解:M甲=32.042,M乙=46.069
50/32.042
X甲醉=0.58979:
P甲=P甲x甲=83.4×0.58979=49.19kPa
50/32.042+50/46.069
P乙醇=P乙醇(1-x甲醇)=47.0(1-0.58979)=19.28kPa
P甲醇49.19
y甲醇=0.718
y乙=1-y=1-0.718=0.282
P甲醇+P乙醇49.19+19.28
4-580℃時純苯的蒸氣壓為100kPa,純甲苯的蒸氣壓為38.7kPa。兩液體可形成理想
液態混合物。若有苯-甲苯的氣-液平衡混合物,80℃時氣相中苯的摩爾分數y=0.300,求
液相的組成。
解:x笨py笨P苯X苯+P甲(1-x)y米
P笨P笨
P甲苯y38.7×0.3
X笨=0.142:x=1-x=0.858
P苯+P甲苯y苯-p苯y苯100+38.7×0.3-100×0.3
4-6在18℃,氣體的壓力為101.325kPa下,1dm的水中能溶解0:0.045g,能溶解
N:0.02g。現1dm將被202.65kPa空氣飽和了的水溶液加熱沸騰,趕出所溶解O的和N,并
干燥之,求此干燥氣體在101.325kPa、18℃下的體積及組成。設空氣為理想氣體混合物,
其組成(體積百分數)為:(O2)=21%,(N2)=79%
解: Mo=31.9988, MN=28.0134
mos
Po,=Kca,Co,.Me
PO2V液Mo2101.325×1×31.9988kPa·dm3·mol-1=72.05×103kPa·dm3·mol-1
mo0.045
PN2V液MN2101.325×1×28.0134kPa.dm3.mol=14.19x104kPa.dm3-mol
mN0.02
202.65kPa空氣中:Po, =202.65×0.21kPa=42.56kPa
PN=202.65×0.79kPa=160.1kPa
1dm3溶液中:42.56
no2Posmol.dm3=5.907×10mol. dm3
ke.o72.05×10
PN 160.1
LN2mol.dm3=11.28×10mol.dm3
k14.19×10
所以V=nRT/p=(no +nN)RT/p={(5.907+11.28)×104×8.314×291.15/101325}m3=41.1cm3yo2 =no (no2+nN2)=5.907/(5.907+11.28)=0.344
yN2=1-yo2=0.656
4-720C下HC1溶于苯中達平衡,氣相中HC1的分壓為101.325kPa時,溶液中HC1
的摩爾分數為0.0425,已知20℃時苯的飽和蒸氣壓為10.0kPa。若20℃時HC1和苯蒸氣總
壓為101.325kPa,求100g苯中溶解多少HC1.
解:kHCt=PHC/xHC=(101.325/0.0425)kPa=2384kPa
P=P苯+PHC1=P苯(1-XHC1)+kx,HC1XHC
xnC=-P101.325-10.0=0.03847
Mc=34.461,M=78.113,W=100g
Xact=(muc1/Mact)/{(mac/Mac1)+(m/M苯)}
MHCm苯xHC36.41×100×0.03847
所以mc=M(1-x)78.113(1-0.03847)
=1.867g
4-8H、N1與100g水在40℃時處于平衡,平衡總壓力為105.4kPa。平衡蒸氣經干燥
后的組成為體積分數(H,)=40%。假設溶液的水蒸氣可以認為等于純水的蒸氣壓,即40℃
時的7.33kPa。已知40℃時H:、N在水中亨利常數分別為7.24GPa及10.5GPa。求40℃時水
中溶解H和N2的質量
:Pn.=(p-Pn.o)×0.40=(105.4-7.33)×0.40kPa=39.23kPa
PN2=P-PH2-PH2=(105.4-7.33-39.23)kPa=58.84kPa
MH=2.0158, MN=28.0134
PHmH2
IMmH
IM
H
XHmH、O
/MHO+mHIMH2+mNIMmH20IM
H.O
PH,mH,oMH.39.23×100×2.0158
mHg=60.6μg
k.R.M.
H,o7.24×10×18.015
PN,MH,OM58.84×100×28.0134
mN.Og=871g
10.5×10×18.015
4-9試用吉布斯-杜亥姆方程證明在稀溶液中溶質服從亨利定律,則溶劑服從拉烏爾定
律證:p=kxu2=u2+ RT In x
du2 = RTdx2 x2(恒溫、恒壓)
x2du2=RTdx2(恒溫、恒壓)
聯立得:
x,du=-x,dus(恒溫、恒壓)
x,du,=-Ridx,=-RTa(l-x)=RTdx,
du1=RTdx1Ix1
du =RTd In x
=A+RT In x,=Hi(p8)+RT In(pi/p)+RT In x
=(P8)+RT In(p,/p)
比較上述兩式可得
P1=Px
4-10A、B兩液體能形成理想液態混合物。已知在t時純A的飽和蒸氣壓p=400kPa,純B的飽和蒸氣壓p=120kPa
(1)在溫度t下,于氣缸中將組成為y(A)=0.4的A、B混合氣體恒溫緩慢壓縮,求凝結出第一滴微細液滴時總壓及該液滴的組成(以摩爾分數表示)為多少?
(2)若將A、B兩液體混合,并使此混合物在100kPa、溫度t下開始沸騰,求該液態混合物的組成及沸騰時飽和蒸氣的組成(摩爾分數)?
解:(1)p1=px=Py
D-Pix1PixAPixm
y yA yA
40x/0.4=120x/0.6聯立求解得:x=0.6667.x=0.3333
XA+XB=1
p=P1.x140×0.6667kPa=66.67kPa
y0.4
(2)p=PAxA+Px={40xA+120(1-xA)]kPa=100kPa
所以有x=0.25,x=0.75
yA=PAXA=40×0.25
=0.1. y'=0.9
PA100
4-1125℃下,由各為0.5mol的A和B混合形成理想液態混合物,試求混合過程的△V、△H、△S及△G。
解:VB=Vm,HB=H△V=0,△H=0
AS=-∑=(-2×0.5×8.314ln0.5)J·K=5.76J·K
△G=AH-TAS=-TAS=-298.15×5.76J=-1.72kJ
4-12苯與甲苯的混合液可視為理想液態混合物,今有一混合物組成為x(苯)=0.3.x(甲苯)=0.7,求在25℃、100kPa下1mo1該混合物的標準熵、標準生成焓及標準吉布斯函數,所需25℃的熱力學數據如表所示
物質AH (kJ-mol)
A,G/(kJ·mol-1)SI(J-K-mol-)
CH(1)48.66
123.0
172.80
CHCH(1)12
114.15
219.58
解:混合物的標準熵:
S(298K)=xSB+xBRlnxB={0.3×172.8+0.7×219.58
-(0.3×8.314xIn0.3+0.7×8.314In0.7)}J-K-mol=211J.K.mol
混合物的標準生成焓
AH(298K)=AH(298K)+AH
=(0.3×48.66+0.7×12+0)kJ.mol=23.0kJ.mol
混合物的標準生成吉布斯函數
A,G(298K)=∑xB△GB(298K)+AmG
∑xB△GmB(298K)+298.15K∑x
0
=[0.3×123+0.7×114.15+298.15×8.314(0.3×In0.3
+0.7In 0.7)x103}kJ.mol=115.3kJ.mol
4-13液體B與液體C可以形成理想液態混合物。在常壓及25℃下,向總量n=10mol,組
成x=0.4的B,C液態混合物中加入14mol的純液體C,形成新的混合物。求過程的△G,
△S。
解:原理想液態混合物總量為n=10mol,組成x=0.4:新的混合物總量n=24mol,
x=18/24=0.75,xB=0.25。設計如下途徑求過程的△G,△S:
n=10mol,x=0.4x=0.75
△SXB=0.25
14mol純Cn=24molC
△SI△S2
6mol純B
18mol純C
△S=△S2-△S1={--R(6×In0.25+18×In0.75)
+R(6×ln0.6+4×ln0.4)}J·K=56.25J·K
△G=-T△S={-298.15×56.25}J=-16771J=-16.77kJ
4-14液體B與液體C可以形成理想液態混合物。在25℃下,向無限大量組成x=0.4
的混合物中加入5mol的純液體C。(1)求過程的△G,△S.(2)求原混合物中族分B和C
的△GB和△Gc。
解:設無限大量的混合物中液體B的物質的量為bmol及液體C的物質的量為cmol.
設計如下途徑求過程的△G,△S:
(b+c)mol,x2=0.4x=0.4
△SXB=0.6
5mol純Cn=(c+5+b)mol
△S△S
bmol純B
(c+5)mol純C
△S=△S:-△S:={--R[(c+5)xIn0.4+bxIn0.60)
+R(cxIn0.4+bxln0.6)} J·K={-5Rln0.4} J·K
=38.1 J-K
△G=-T△S=(-298.15×38.1}J=-11360J=-11.36kJ
(2)混合前:Sc=S-RInxc=S-RIn0.4
混合后:S=S-RIn04(b+c)+5共有0.4(b+c)mo1=0.4Nmol
b+c+5
0.4(b+c)+50.4N+5
ASc.m=Sc-Sc=RIn=RIn
0.4(b+c+5)0.4N+2
Ase =0.NR In -0.4R l m Nin O aN3-3R
0.4N+2
△Gc =-TASc=3RT=7.44KJ
混合前:SB=S-Rlnx=S-Rln0.6
混合后:SB=Sm.B-RIn0.6(b+c)共有0.6(b+c)mol=0.6Nmol
b+c+5
0.6(b+c)0.6N
AS B.m=SB-SB=RIn=RIn
0.6(b+c+5)0.6N+3
O.6N-=0.6R lim Nin-0.6N
AS =0.6NR In3R
0.6N+30.6N+3
△G=-TAS=-3RT=-7.44KJ(這種解法僅供參考)
4-15在25C向1kg溶劑A(H:0)和0.4mo1溶質B形成的稀溶液中又加入1kg的純溶劑,若溶液可視為理想稀溶液,求過程的△G
解:設計過程如下
lkg H2O,bB=0.4mol/kgbB=0.2mol/kg
△G(溶質)+△G(溶劑)2kgH2O
lkg純H2OnB=0.4mol
△G:(溶質)+△G:(溶)△G2(溶質)+△G2(溶劑)
0.4mol純B
2kg純H2O
先求算溶劑的△G(溶劑):因為△G=GA)-GAD=μA-μAD=RTInXA
所以有
△G(溶劑)=△G1(溶劑)-△G1(溶劑)
={8.314×298.15×(111.12×ln111.1255.56
-55.56×In)}J
111.5255.96
=-1.70J
對于溶質,因為△G=GB(溶質)GB(溶質)=μB(溶質)μB(溶質)
= RT Inb /b
△G(溶質)=△G1(溶質)-△G1(溶質)
={8.314×298.15×(0.4×ln02.-0.4×ln0.4}J=-687.3J
所以△G=△G(質)+△G(列)=-687.3J+(-1.7J)≈-689J
4-16(1)25℃時將0.568g碘溶于50cmCC1中,所形成的溶液與500cm3水一起搖動,
平衡后測得水層中含0.23mmol的碘。計算碘在兩溶劑中的分配系數
K,K=c1(H2O)c1(CCl)設碘在兩相溶劑中均以I分子形式存在
(2)若25C時碘I:在水中的濃度是1.33mmoldm,求碘在CC1中的濃度。
解(1)n1=m/M1=(0.568/253.809)mol=2.2379×10mol
2.33×10/500
K=-=0.0116
(22.379×10-2.33×104)/50
(2)c1(CCl4)=c1(H2O)/K=1.33/0.0116mol.dm3=115mol.dm3
4-1725C時0.1mo1NH溶于1dm'三氯甲烷中,此溶液NH的蒸氣分壓為4.433kPa,同
溫度時0.1mo1NH溶于1dm水中,NH的蒸氣分壓為0.887kPa。求NH在水與三氯甲烷中的
的分配系數K,K=CNH(H2O)CNH(CHCl3)
4.433
解:kx3(CnC)=kPa-dm3-mol1=44.33kPa-dm3-mol-1
0.1
K.w,,0 .1 kPa dm mol'=8.87kPa"
0.887
兩相平衡時;PNH3 =ke.NH3(H0)CNH3(H-0) =ke.NH,(CHCI3)CNH3(CHC3)
K=,(H,O/,()-SC CM-889 =s.
4-1820℃某有機酸在水和乙醚中的分配系數為0.4.今有該有機酸5g溶于100cm水
中形成的溶液。
(1)若用40cm乙醚一次萃取(所用乙醚已事先被水飽和,因此萃取不會溶于乙醚)
求水中還剩下多少有機酸?
(2)將40cm乙醚分為兩份,每次用20cm乙醚萃取,連續萃取連次,問水中還剩
下多少有機酸?
解:(1)m/100
(5g-m)/40=0.4, 求得m=2.5g
(2)m, /100
0.4
(5g-m,)/20
m2/100=0.4
(m,-m2)/20聯立解得:m,=2.22g
4-19 25g 的 CC1. 中溶有 0.5455g 某溶質,與此溶液成平衡的 CC1. 蒸氣分壓為
11.1888kPa,而在同一溫度時純CC1.的飽和蒸氣壓為 11.4008kPa.(1)求此溶質的相對摩
爾質量 Mr. (2)根據元素分析結果,溶質中含 C為 94.34%,含日為5.66%(質量百分數),
確定溶質的化學式。
解:(1)px= pAxx=pA(l-xg)
x = PΑ-PΑ =m,IM,
m/M,+mIMA
m,MAPA_0.5455×153.823×11.1888= 178
:. M,mx(pA-pA) 25(11.4008-11.1888)
(2) 1mol溶質B中,含C元素的物質的量
n= (178 × 0.9434/12.011) mol ≈ 14mol
含 H 元素的物質的量
n= (178 × 0. 0566/1. 0079) mol 10mol
所以,溶質 B 的化學式為:C4H
4-20 10g 葡萄糖(CHz0c)溶于 400g 中,溶液的沸點較純乙醇的上升 0.1428℃,另外
有 2g 有機物溶于 100g 乙醇中,此溶液的沸點上升 0. 1250℃,求此有機物的相對摩爾質量。
10×103
解:b=mol·kg'=0.1388mol·kg
180.157×400
K.=0.1428 K-mol-kg=1.029K-mol-kg
又有 ΔT = K,b =K2 mol = κ 20 molkg
M=20 mol-k- 20x1029 = 165
4-21 在 100g 苯中加入 13.76g 聯苯(C.H.C.Hs),所形成溶液的沸點為 82.4℃.已知純
苯的沸點為 80.1℃.求:(1)沸點升高常數;(2)苯的摩爾蒸發熱。
解:(1)△T,=982.4-80.1)K=2.3K
b=154.21xo mol-kg= 0.8923mol-kg1
,=2Kmol-kg=2.58K-mo-kg
(2) K,=R(T)M,/△HA
ΔηΗΑ=R(T)MA_8.314×353.252×78.113
J·mol-' = 31.4kJ·mol
K2.58
4-22 已知0℃、 101.325kPa時, 02在水中的溶解度為4.49cm//100g (H0); N:在水中
水中的溶解度為 2.35cm//100g(H20),試計算被 101.325kPa 空氣(含 N279%,0:21%,均為體積百分數)所飽和了的水的凝固點較純水的降低了多少?
101.325×103 ×4.49×10*
解: Po, =koo,bo, =ko8.314×273.15×100-x10' mol-kg =101.325x10 Pa
8.314×273.15×100
kp.o, =4.49×10-3
Pa·mol-'·kg = 50.578×10'kPa·mol-'·kg
8.314×273.15×100
Kb.Nz2.35×10
Pa·mol·kg = 96.637×10 kPa·mol·kg
by=bo, +bN, = Po, Ikso, + PN, /koN,
=[101.325×0.21/(50.578×10)+101.325×0.79/(96.637×10)mol.kg-
=1.249×10mol'·kg
所以,△T=Krbs=1.86×1.249×10-K=2.32×10K
4-23 已知樟腦(CaHs0)的凝固點降低常數 K-40K- mol".kg。(1) 某一溶質相對摩爾質量為 210,溶于樟腦形成質量百分數 5%的溶液,求凝固點降低多少?(2)另一溶質相對摩爾質量為 9000,溶于樟腦形成質量百分數 5%的溶液,求凝固點降低多少?
解:(1)b=3x10mol-kg=0.25mol-kg-; △Tr=Krbo=40×0.25K=10K
(2) b=xosmol-kg=5.848×10-mol-kg-; △Ti=Krb=40×5.848×10"k=0.234K
4-24 現有蔗糖(CHz0n)溶于水形成某一濃度的稀溶液,其凝固點為-0.200℃,計算此溶液在 25℃時的蒸氣壓。已知水的 Kr=1.86K· mol·kg,純水在 25℃時的蒸氣壓為PH,o =3.617kPa.
解b.-0.200 mol-kg = 0.10733mol-kg
= 1.9334x10
0.10753
0.10753+1000/18.015
РH.о = РH,0)*н,о =3.167(1-1.9334×10-)kPa = 3.161kPa
4-25 在 25℃時,10g 某溶質溶于 1dm’溶劑中,測出該溶液的滲透壓 1=0. 400kPa,確定該溶質的相對摩爾質量。
解: IV =nRT=RT
mRT 10×8.314×298.15
M=IV0.4000×1
g·mol-' =6.24×10*g·mol-
M, =6.20×10
4-26 在 20℃下將 68.4g 蔗糖(CHz0n)溶于 1kg 水中.求:(1)此溶液的蒸氣壓;(2)此溶液的滲透壓。已知 20℃下此溶液的密度為 1.024g·cm',純水的飽和蒸氣壓Pн,o = 2.339kPa.
解:(1)1000/18.015
Xн.о68.4/342.299+1000/18.015=0.9964
PH20 = PH2ouxH20 =2.339×0.9964kPa =2.33kPa
(2)V=m 68.4+1000×106m3=1.0434×10-3m3
p1.024
∏=nRT68.4×8.314×293.15Pa=467kPa
V342.299×1.0434×10
4-27人的血液(可視為水溶液)在101.325kPa下于-0.56℃凝固。已知水的
K=1.86K·mol·kg。求(1)血液在37℃時的滲透壓;(2)在同溫度下,1dm蔗糖(CH:01)
水溶液中需含多少克蔗糖時才有能與血液有相同的滲透壓。
解:(1)b=AT_056mol·kg1=0.3011mol·kg
1.86
對于稀溶液,c≈b=0.3011mol-kg;I1=cRT=0.3011×8.314×310.15kPa=776kPa
(2)m=Mc=342.299×0.3011g.dm=103 gdm
4-28在某一溫度下,將碘溶解于CC1:中,當碘的摩爾分數x,在0.01-0.04范圍內時
此溶液符合稀溶液規律。今測得平衡時氣相中碘的蒸氣壓與液相中的碘的摩爾分數之間的兩
組數據如下:1.638
16.72
P1 IkPa0.03
0.5
X1
求x13
=0.5時,溶液中碘的活度a,及活度系數
解:根據亨利定律: P1 =k1x1;k=P1/x1 =(1.68/0.03)kPa=54.6kPa
當
X=0.5: a1 = P11k =16.72/54.6=0.306. 13 =a1 1x1=0.306/0.5=0.612
第五章 化學平衡
5-1 在某恒定的溫度和壓力下,取 n。 = lmol 的 A(g)進行如下反應:
A(g) = B(g)
若μ=μ,試證明,當反應進度ξ=0.5mol時,系統的吉布斯函數G值為最小,這時A,
B 間達到化學平衡
證明:A(g)= B(g)
設開始時,A 的物質的量為 nA.0,B 的物質的量為 ng.0,而反應過程中 A.B 的物質的量分別量
為nA與ng,此時系統的吉布斯函數為
dG = (με - με)dξ
設反應從A 開始時 nAo=1mol ,當反應進度ξ=0.5mol 時,n,=ng =0.5mol ,
Σng=1mol, pA = Pg =0.5p 及μ=μβ代入上式得
dG = (μα - μa)dξ = ((μ% + VRT In pg)-(vμ° + RT In pA)}dξ
={(μ-μ)+(RT In pa-RT In pA)}dξ =0
OG
或Α=
=0
這就證明了若 μ= μ,反應進度ξ=0.5mol 時,系統的吉布斯函數 G 值為最小,此時
A=OG
=0,A,B 間達到化學平衡。
ξ
5-2 已知四氧化二氮的分解反應
N204(g)=2NO2(8)
在298. 15K 時, A,G=4.75kJ-mol-.試判斷在此溫度及下列條件下,反應進行的自發方向:
(1) N2O,(100kPa), NO,(1000kPa); (2) N2O,(1000kPa), NO2(100kPa);
(3) N20,(300kPa), NO2(200kPa).
解: In K=-A,GIRT=-4.75x103/(8.314x298.15)=-1.9283,K° =0.1454
(1) (P)(100/100)2- = 100
100/100J, > K°,反應向左;
(2)_(PNo, /p°)_(100/100)
PN,o,/p° 1000/100=0.1,J,<K°,反應向右;
(3)(Pso, /p°)_(200/100)=1.333,
PN,o, Ip°300/100J,>K°,反應向左。
5-3 1000K時,反應C(s)+2H2(g)=CH,(g)的A,G=193797J-mol-1.現有與碳反應
的氣體,其中含有φ(CH.)=0.10,φ(Hz)=0.80,φ(Nz)=0.10.試問:(1)T=1000K,
p=100kPa 時,△,G等于多少,甲烷能否形成?(2)在 T=1000K 下,壓力需增加到若干,
上述合成甲烷的反應才能進行?
解:先求反應的標準平衡常數
In K° =-Δ,GIRT =-19397/(8.314x1000),K° =0.097
1
-= 0.1563,
A,G= RT In(J,IK°)= (8.3145x1000In(0.1563/0.097)) = 3963J >0(
向左,甲烷不能形成J,> K°),反應
(2)只有J,≤K①時,才能形成甲烷:
p×0.1/100kPa<0.097,解得 p>161.1kPa
(p×0.8/100kPa)
5-4 已知同一溫度,兩反應方程及標準平衡闡述如下:
C(石墨)+H20(g)=CO(g)+H2(g)K
C(石墨)+2H20(g)=CO2(g)+2H2(g)K2
求下列反應的 K°.CO(g)+H20(g)=CO2(g)+H2(g)
解:已知如下三個反應:
(1)C(石墨)+H20(g)=CO(g)+H2(g)K
(2)C(石墨)+2H20(g)=CO2(8)+2H2(8)K
(3) CO(g)+H20(g)=CO2(g)+H2(g)K°
顯然 (3)= (2)-(1)
因而有Δ,G = Δ,G-Δ,G
故得K°= K/K
5-5 已知同一溫度,兩反應方程及標準平衡闡述如下:
CH,(g)+CO2(g)=2C0(g)+2H2(g)K
CH,(g)+H20(g)=CO(g)+3H2(8)
求下列反應的 K°.Kg
CH,(g)+2H,0(g)=CO2(g)+4H2(8)
解:已知如下三個反應:
(1)CH (g)+CO2(g)=2C0(g)+2H2(8)K
(2) CH (g)+H20(g)=CO(g)+3H2(g)K
(3) CH,(g)+H20(g)=CO(g)+3H2(g)K
顯然 (3)=2x (2)-(1)
因而有Δ,G = 2Δ,G2 - Δ,G.
K°= (
故得K
5-6 在一個抽空的容器中引入氯和二氧化硫,若它們之間沒有發生反應,則在375.15K
時分壓分別為47.836kPa和44.786kPa.將容器保持在375.15K,經一定時間后,壓力變為
常數,且等于86.096kPa.求反應SO,Cl,(g)=SO,(g)+Cl2(g)的K".
解:平衡時:Σpr=ps
Pso,C1+(44.786kPa-Pso,c,)+(44.836kPa-Pso,a,)=86.096kPa
Pso,cl,= 6.526kPa
Ps=44.786kPa-6.526kPa=38.26kPa
Pa:=47.836kPa-6.526kPa=41.31kPa
:. K° = Pso, "Pa, (Pso,a, P°)= 38.26x41.31/(6.526x100) = 2.42
5-7 使一定量 1:3 的氮、氫混合氣體在 1174K, 3Mpa 下通過鐵催化劑以合成氨。設反
應達到平衡。出來的氣體混合物緩緩地通入20cm,鹽酸吸收氨。用氣量計測得剩余氣體的體
積相當于273. 15K, 101. 325kPa的干燥氣體(不含水蒸氣) 2.02d m'.原鹽酸溶液20cm'需
用濃度為52. 3mmol .dm'的氫氧化鉀溶液18.72cm'滴定至終點.氣體通過后則需用同樣濃度
的氫氧化鉀溶液15.17cm'.求1174k時反應N2(g)+3H2(g)-2 NH,(g)的K0.
解: nNH,=52.3x10-(18.72-15.17)×10-mol=0.1857×10-mol
n,In, =1/3
пN, +лн, = pV/RT =[101.325x 2.02/(8.314x273.15)]mol = 90.13x10-mol
nH, =67.60×10-3mol
ng =N, +H, +NH, = 90.323x10mol
n,=22.53×10-'mol,
22.53
PN,=PeXN, =3000xkPa = 748.3kPa
90.32
PH: =PaX, =3000x 67.60 kPa=2245kPa
PNH,=(3000-748.3-2245)kPa=6.7kPa
:. K°= pn, p02 (p, p,)= (6.7x100)2 /(748.3x2245°)=5.3x10-8
5-8 五氯化磷分解反應 PCl,(g)=PCl,(g)+Cl,(g)在 200℃時的 K°-0.312,計算:(1)
200℃、200kPa下 PC1,的離解度;(2)組成1:5 的 PC1,與C1:的混合物,在200℃、101.325kPa
下 PCI,的離解度。
解:平衡時各物質的設為
Rpc, =(1-α)mol, Hpci, =amol, na, =conol, ng=(1+a)mol, pa=200kPa-20003解得α=36.7%
(2)平衡時各物質的量設為npa,=(1-a)mol, npc,=camol, na,=(5+a)mol,,ng =(6+α)mol, p s=101. 325kPa
κ"=α(5+α) Peα(5+α) 101.325=0.312解得α=26.8%
(6+α)(1-α) p° (6+α)(1-α) 100
5-9在994K,使純氫氣慢慢地通過過量的Co0 (s),則氧化物部分地被還原為Co (s).
流出來的平衡氣體中氫的體積分數 φ(Hi) =2.50%.在同一溫度,若用 CO 還原 Co0(s),
平衡后氣體中一氧化碳的體積分數 φ (CO)=1. 92%. 求等摩爾的一氧化碳和水蒸氣的混合物
在 994K 下,通過適當催化劑進行反應,其平衡轉化率為多少?
解: H,(g)+CoO(s) Co(s)+H,O(g)
平衡時 2.50%97.5%
K=97.5/2.50 =39.0
CO(g)+CoO(s) Co(s)+CO2(g)
平衡時 1.92%98.08%
K,=98.02/1.92=51.08
由反應(2)-(1)得
CO(g)+H,0(g)994KH2(8) + CO2(8)
平衡時 (1-α) mol (1-α)mo1amol
amol
α = 53.4%
5-10 在真空的容器中放入故態的 NH.HS,于 25℃下分解為 NH,與 H.S,平衡時容器內的
壓力為 66.66kPa.(1)當 入 NH.HS 時容器中已有 39.99kPa 的 HS,求平衡時容器中的壓力;
(2)容器中原有 6.666kPa 的 NH,問需多大壓力的 HS,才能形成 NH.HS 固體?
解:(1) NH.HS HS(g)+ NH,(g)
初始分壓
平衡分壓39.99kPa
p+39.99kPa p
K" = p(p+33.99kPa)/ po
K° =
66.66kPa 66.66kPa /po'= p(p+33.99kPa)/po
33.33kPa2 = p(p+33.99kPa)
p = 18.87kPa: P =2p+39.99kPa = 77.7kPa
(2)只有J,2K°時,才能形成NH.HS:
6.666kPa PH 2 33.33°kPa'/p 解得PHs>166kPa
5-11 現有理想氣體間反應 A(g)+B(g)=C(g)+D(g),開始時,A與B 均為1mo1,25℃時,反應達到平衡時,A 與 B 的物質的量各為⊥mol·(1)求此反應的 K°;(2)開始時,A 為 1mol,B 為 2mol;(3)開始時,A 為 1mol,B 為 1mo1,C 為 0.5mol;(4) 開始時,C為1mol ,D 為 2mol。分別求反應達到平衡時 C 的物質的量。
解:(1)k°=-()) -4
(2) к°=4=
(1-x)(2-x)x =0.845 即nc =0.845mol
(3) K°=4=(0.5+x)x
(1-x)2x=0.596 即ne =(0.5+x)mol=1.096mol
(4) к°=4=(1-x)(2-x)
2x=0.457 即n =(1-x)mol =0.543mol
5-12 將 1molSO2與 1mo10:的混合氣體在 101.325kPa 及 903K 下通過盛有鉑絲的玻璃管,控制氣流速度,使反應達到平衡,把產生的氣體急劇泠卻,并用KOH吸收SO,及SO,最后量得余下的氧氣在101. 325kPa, 273. 15K下體積為13. 78dm',試計算反應so,+o,=so,在 903K 時的A.G°及 K°.
解: no,=pV/RT=[101.325x13.78/(8.314x273.15)]mol=0.615mol
nso, =2(1-0.615)mol = 0.77molnso, = (1-0.77)mol = 0.23mol
ng =(0.615+0.23+0.77)mol =1.615mol
K°=0.77×1.6152×1002=5.39
0.23×0.6152 ×101.3252
A,G=-RT In K =(-8.314×903In 5.39)J -mol'=-12.65kJ-mol'5-13383.15K、60.483kPa時,從測定醋酸蒸氣的密度所得到的平均摩爾質量是醋酸
單分子摩爾質量的1.520倍。假定氣體分子中含有單分子及雙分子。求下列反應的A.G
2CH3COOH=(CH3COOH)
解:設蒸氣中雙分子的摩爾分數為x,單分子摩爾質量為M
(1-x2)M1+x22M=1.52x2=0.52
Mi
K=60.483×0.52/100=3.73
[60.483×(1-0.52)/100]
A.G=-RT In K =(-8.314×383.3In 3.73)J-mol '=-4.2kJ-mol5-14(1)在1120℃下用H:還原Fe0(s),平衡時混合氣體中H的摩爾分數為0.54.
求Fe0(s)的分解壓。已知同溫度下
2H2O(g)=2H2(g)+O2(g)K=3.4×101
(2)在煉鐵爐中,氧化鐵按如下反應還原
FeO(s)+CO(g)=Fe(s)+CO2(g)
求1120℃下,還原1moLFe0起碼需要CO若干摩爾?已知同溫度下
2CO2(g)=2CO(g)+O2(g)K=1.4×10-2
解:(1)H2(g)+FeO(s)1120→H2O(g)+Fe(s)(1)
平衡時:yu2=0.54yH2o=0.46
K=0.46/0.54=0.852
2H2O(g)-1120C2H2(g)+O2(g)(2)
K=(3.4×10-)
由反應(1)+(2)得
Feols)-1ame5o.(8)+Fels)
K=KK=0.852×(3.4×10)
K0=(Po2 Ip0)/
Po=0.852×3.4×10-3×100kPa=2.47×10kPa
(2)FeO(s)weO(g)+Fe(s)(3)
K=4.968×10
CO2(g)→CO(g)+O2(g)(4)
K=(1.4×10-2)
由反應(3)-(4)得
FeO(s)+CO(g)1120)CO2(g)+Fe(s)K=K
o/K.
1=0.42
初始時1mol
n
0
0
平衡時n-1mol
1mol
1mol
K=K/K=0.42=
Imoln=3.38mol
n-Imol
所以起碼需要CO的物質的量為3.38mo1.
5-15求下列反應在298.15K下平衡的蒸氣壓:
(1)CuSO4-5H2O(s)=CuSO43H2O(s)+2H2O(g)
(2)CuSO43H2O(s)=CuSO4.H2O(s)+2H2O(g)
(3)CuSO4H2O(s)=CuSO4(s)+H2O(g)
已知各物質的標準摩爾生成吉布斯函數AG(298K)如下:
物質CuSO45H2O(s)
CuSO-3H2O(s)
CuSO4H2O(s)
CuSO(s)
H2O(g)
4G-1879.6
-1399.8
-917.0
-661.8
-228.6
kI.mol'
解:(1)A.G=[2(-228.6)+1×(-1399.8)-1×(-1879.6)]kJ.mol =22.6kJ.mol
AG=-RT In K =-RT In(p p)2
22.6×103=-8.314×298.151n(p/p)2
p=1.05kPa
(2)A.G=[2(-228.6)+1×(-917.0)-1×(-1399.8)}kJmol-' =25.6kJmol-'
AG=-RT In K=-RT In(p/ p)2
25.6×103=-8.314×298.15In(p/p)2
p=0.57kPa
(3)AG={(-228.6)+1×(-661.8)-1×(-917.0)}kJ-mol =26.6kJ.mol
A.G=-RTIn K=-RT In(p/p)
26.6×103=-8.314×298.151n(p/p)
p=2.2×103kPa
5-16已知下列數據(298.15K):
物質C(石墨)
H(g)
N(g)
0:(g)
CO(NH2)2(s)
S(298K)5.740
130.68
191.6
205.14
104.6
Jmol-1.K-
A.H(298K)-393.51
-285.83
0
0
-631.66
kJ.mol
物質NH3(g)
CO:(g)
H0(g)
AG(298K)-16.5
-394.36
-228.57
kJ·mol-
求298.15K下CO(NH:):(s)的標準摩爾生成吉布斯函數A,G以及下列反應的標準平衡常數KCO2(g)+2NH2(g)-H2O(g)+CO(NH2)2(s)
解:C(石墨)+O2(g)+Nz(g)+2H(g)-25C→CO(NH2)2(s)
A.S(298K)=(1×104.6-1×5.740-0.5×205.14-1×191.6-2×130.68)J.mol.K
=-456.67J-mol-K
A.H(298K)={1×(-393.15)+2×(-285.83)-1x(-631.66)}kJ.mol'.K=-333.51kJ.mol.KAG[CO(NH2)1,(s).298K]=A,H(298K)-298.15K×A,S(298K)
={-333.51-298.15×(-456.67)×103}kJmol=-197.4kJ.mol
CO2(8)+2NH3(8)-2cH2O(8)+CO(NH2)2(s)
A.G[298K]={1×(-197.4)+1×(-228.57)-1x(-394.36)-2×(16.5)]kJ·mol=1.39kJ.mol
In K"=-A,G[298K]/(R×298.15K)=-1.39×103/(8.314×298.15)=-0.5608
K=0.571
5-17已知25C時AgCl(s),水溶液中Ag,C1的AG分別為-109.789kJ·mol,77.107kJ·mol,-131.22kJ·mol'。求25C下AgCl(s)在水溶液中的標準溶度積K及溶解度s
解:溶解反應方程為
AgCl(s)=Ag'+Cl
bb
△,G =AG(Ag+)+△,G(Cl)-△,G(AgCl)={77.107+(-131.22)-(-109.789)}=55.676
-55676
In K=-AG RT=-22.4593
8.3145×298.15
K=1.763×1010
K=1.763×1010=(b1b0)2
所以b/b0=√1.7632×105=1.3279×10;b=1.3279×10molkg
AgC1的摩爾質量為143.32g,所以,
s=13.279× 10× 143.32·kg'=0.00190g/1000g=0.019g/100g
5-18利用附錄十附錄十一的數據計算25℃水溶液中碳酸解離反應的K,K
H2CO3=H*+HCO3K
HCO3=H*+CO3K
解:由附錄十、附錄十一得
A G I(kJmol)A H I(kJ.mol)S (J.K--mol)
H2CO3-623.08
-699.65
187.4
HCO3-586.77
691.99
91.2
co?-527.81
677.14
-56.9
H2CO3=H+HCO3K
A,G=AG(HCO3)-A,G(H2CO3)={-586.77-(-623.08)]kJ=36.31kJ
In K=-A,G RT=-36310=-14.647
8.3145×298.15
K=4.35×107HCO3=H*+CO3K
A,G=AG(CO3)-A,G(HCO3)={-527.81-(-586.77)}kJ=58.96kJ
In K=-A,G RT=
-58960-=-23.784
8.3145×298.15
K=4.685×10
(由AH及S求AG,進而求K及K略)
5-19利用附錄十、附錄十一的數據計算25℃水溶液中配離子[Ag(NH3)2]*如下反應的
不穩定常數K0。lAg(NH,)2J-Ag+2NH.
解:由附錄十、附錄十一得
A G I(kJ.mol)A H I(kJ.mol)S (J.K--mol)
Ag77.107
105.579
72.68
NH3-26.50
-80.29
111.30
[Ag(NH3)2]*-17.12
-111.29
245.2
A,G=AG(A8)+2AG(NH3)-AG([Ag(NH3)2])
=(77.107+2×(-26.50)-(-17.12)}kJ=41.227kJ
In K=-A,G RT=-41227=-16.6307
8.3145×298.15
K0=5.9×108
(由AH及S求AG,進而求K略)
5-20已知298.15K時, CO(g)和CH:OH(g)AH分為-110.52和-200.7kJ·mo1'CO(g)、H:(g)、N:(g)、CHOH(1)的S0分別為197.67、130.68、127J·mol·K又知298.15K時甲醇的飽和蒸氣壓為16.59kPa,A_H_=38.0kJmol3,蒸氣可視為理想氣體。利用上述數據,求298.15K時反應CO(g)+2H2(8)=CH3OH(g)的A,G及K
解:據題意畫出如下方框圖:
CHOH(1)△S
CHOH(1)
△S:
CHOH(g)
△S3
CHOH(g)
298K,298K,
298K,
298K,
100kPa16.59kPa
16.59kPa
100kPa
1mol1mol
1mol
1mol
S[CH3OH(1),298K]S[CH3OH(g),298K]
=127J.mol.K=?
△S1≈0
△S=△H/T=(38.0×103/298.15)J·molK=127.45J-molK
△S=[8.3141n (16.59/100)} J. mo1'K'--14. 94 J.mol.K
S[CH3OH(g),298K]=S[CH3OH(1),298K]+AS1+AS2+AS
=(127+0+127.45-14.94)J.mol.K=239.51J.mol.K-
CO(g)+2H2(g)-CCH3OH(g)
A.G(298.15K)=A.H(298K)-298.15K×AS(298.15K)
={-200.7-(-110.52)-298.15×(239.51-2×130.68-197.67)×103}kJ.mol
=-24.73kJmol
In K"=-A,G[298K]/(R×298.15K)=24.73×103/(8.314×298.15)=9.976
K=2.15×10
5-21在高溫下水蒸氣通過灼熱的煤層,按下式生成水煤氣:
C(石墨)+H2O(g)=H2(g)+CO(g)
若在1000K及1200K時,K分別為2.505及38.08,試計算此溫度范圍內平均反應熱△,H
及在1100K時反應的標準平衡常數K
解:In
#()
A.M.I R i1200×100038.08
×8.314In.mol=135.8kJ.mol
200-10002.505
1100-1000
In K(1100K)=In K(1000K)+△,H
R1100×1000
135.8×101100-1000
=In2.505+=2.403
8.3141100×1000
K(1100K)=11.0
5-22在100℃下,下列反應COCl2(g)=CO(g)+Cl2(g)
的K=8.1×10,AS(373K)=125.6J·mol.K.計算(1)100℃、總壓為200kPa時COCl
的離解度;(2)100℃上述反應的A.H;(3)總壓為200kPa、COCl,離解度為0.1%時之
溫度,設,△,Cm=0.
解:(1)設COCl,的離解度為a
COCl2(g)=CO(g)+Cl2(g)
(1-a)mol a mol a mol
n=(1+α)mol
8.1×10-9=a×2
1-a
a=6.37×10
(2) A.G=-RT In K ={-8.314×373.15In(8.1×10)}J.mol-' =57.84kJ.mol-'△,H=A,G+TA,S
=57.84+373.15×125.6×103kJmol=105kJmol
(3),△C=0,△,H為常數
ki a".
=10×2×101.325/100=2.0×10
()
-()=(8.314
2.0×106
InK
373.15104.7×108.1×10
=446K
5-23 反應
2NaHCO,(s)= NaCO,(s)+H20(g)+CO2(8)
在不同溫度時的平衡總壓如下:
t/℃
p/kPa30
0.82750
70
90
100
110
3.99915.90
55.23
97.47
167.0
設反應的△,H°與溫度無關。
求:(1)上述反應的△,Hg;(2)1g(p/kPa)與T的函數關系式;
(3) NaHCO,(s)的分解溫度。
解:(1)題目給反應的 κ°
K" =2
Ig(p/kPa) =-Δ(+2)-
由題目給數據算出 1/T 及對應的 1g (p/atm)列表如下:
(K/T)10
p/kPa0.827
3.999
15.90
55.23
97.47
167.0
Ig( p/kPa)-0.08250.6020
1.2014
1.7422
1.9889
2.2227
以 1g (p/kPa)對(K/T) 10'作圖:
/d3.2993.095
2.914
2.754
2.680
2.610
1.5
0.5
o
-0.5 00.5
1.5
2.5
3.5
(K/T) ×102
由圖可見,直線的斜率為 m=-△,H°_1.5-(1.0)
4.606RK 2.82-2.97
-×103 =-3.333×103
Δ,H =-4.606RmK =(4.606x8.314x(-3.333x10)JJ-mol- =128kJ-mol-
(2) Ig(ρkPa) A-3
取圖中的 T、p 值代入上式,可以算出:C=10.899; 故Ig(p/kPa)3333+10.899
(3) p=101. 325kPa時對應的T稱為NaHCO,(s)的分解溫度
g(101.325/kPa)3333+10.899T=374K
5-24 在 454~475K 溫度范圍內,反應
2C,H,OH(g)=CH,COOC,H,(g)+2H2(8)
的標準平衡常數K與T的關系式如下:2100
TIK+4.67
lg K°
已知473K時乙醇的△,H=-235.34kJ-mol-1.求乙酸乙酯的A,H(473K).
解:題目給反應的△,H°在 454~475K 溫度范圍內與 T 無關
-Δ,Η°/2.303RK = -2100; Δ,Η° = 2100x2.303x8.314J-mol-' = 40.202kJ- mοl-
Δ,H° =Δ,H°(CH,COOC,H,)-2Δ,H°(C,H,OH)
:. Δ,H°(CH,COOC,H,)= (40.202+2(-235.34)}kJ -mol =-430.5kJ-mol
5-25 已知下列數據S°(298K)Cp./ (J· mol".K"') = a +b (T/K) +c (T/K)
Δ,Η°(298K)
物質kJ·mol
J·mol K
bx10'
c×10°
-110.52197.67
26.537
7.6831
-1.172
H2 (g)130.68
26.88
4.347
-0.3265
CH OH(g)-200.7
239.8
18.40
101.56
-28.68
CO (g)
求反應CO(g)+2H2(g)=CH,OH(g)的1gK°與T的函數關系式及300℃時的K°.
解:根據題目給的數據,計算如下:
Δ,S = (239.8-197.67-2x130.68)x10-kJ -mol--K- =-0.219kJ -mol--K-1
Δ,Η° = (-200.7+110.52)kJ -mol-1 = -90.18kJ-mol-1
Δ,G = Δ,Η° - 298.15KΔ,S =(-90.18-298.15x(-0.219)}kJ -mol-
=-24.885kJ·mol
將△,H°(298K)、 △a、△b及△c值帶土上式后可得
In K =-Δ,G(RT) = 24885/(8.314x 298.15)= 10.039
Δa=(18.40-26. 537-226. 88) J-mol.K=-61.897 J-mol.K"
Ab=(101. 56-7. 6831-2x4. 347)x10 J-mo1.K=85. 183x10 J-mo1"K
Δc=(-28. 68+1. 172+2x0. 3265) x10° J-mol.K-=-26.855x10* J-mol.Kx
Δ.Η = ΔH + ΔaT +ΔbT +T
Δ.Η = -75274.31-mol +ΔαT +ΔbT +ΔT'
將此式代入下式中din K"=A
積分可得
InK-In7274328(n-n298.15)
+(T -298.15K)+ T2 - (298.15K)
將InK2og、 R、 △a、 △b及△c值代入上式,并換成常用對數,整理后可得IgK-3932-7.445Ig(T/K)+2.225x10-(T/K)-0.2338x10-(T/K) +8.94當 T=573. 15K 時由上式可得
所以Ig K?=-3.5376
K"=2.90 × 10*
5-26 反應 3CuCl(g)=Cu,Cl,(g)的△,G°與T的關系如下
Δ,GJ·mol-)=-528858-52.34(TIK)Ig(T /K)+438.2(T /K)
求:(1)2000K 時此反應的△,H°、 △,S°
(2)此反應在 2000K,101.325kPa 下平衡混合物中 Cu;Cl,的摩爾分數。
解: (1) (0A,GI8T), =-△,S=(-52.341g(TIK)
-52.34(T/K)d Ig(T/K)/d(T/K)+438.2)J·mol-·K-
(T/K)d Ig(T/K)/d(T/K)=d lg(T/K)/d In(T /K)=1/2.303
Δ,S =(-52.34Ig(T /K)+52.34/2.303-438.2)J·mol-.K-1
=(-52.34Ig(T /K)-415.5)J-mol-.K-1
當 T=2000K 時
Δ,S =(-52.341g 2000-415.5)J-mol--K-1 =-242.7J-mol-1.K-
Δ,G = 1990.18J -mol-
Δ,Η° =Δ,G +TΔ,S°
= (19990.18+ 2000x(-242.7)}J·mol-=-483.4kJ·mol-
(2) =)=xp-GRT))
=-199018/8.31400
(- =0.911
上述方程式的形式簡單,可用累試法求其近似根,因摩爾分數 y 小于 1,故可先從 0. 5
試起,結果可得y=0.3053
5-27工業上用乙苯脫氫制苯乙烯
CH3C2H3(g)=CH3C2H3(g)+H2(g)
如反應在900K下進行,其K=1.51。試分別計算在下述情況下,乙苯的平衡轉化率:(1)反應壓力為100kPa時;(2)反應壓力為10kPa時(3)反應壓力為101.325kPa,且加入水蒸氣使原料氣中水與乙苯蒸氣的物質的量之比為10:1時。
解:(1)CH3C2H3(g)=CH3C2H3(g)+H2(g)
初始物質的量1mol
0
0
平衡物質的量(1-α)molamo 1
amoln=(1+α)mol
K=x1.51a2100a=77.6%
1-1-a2
100
(2)151=解得
a=96.8%
(3)n=(11+α)mol
K"=-ax-101.325
(1-a)(11+a)p(1-a)(11+a)100
2.52a2+15.1a-16.61=0
a=94.9%
5-28在一個抽空的燒瓶中放很多的NHC1(s),當加熱到340℃時,固態NHC1仍然存在,此時系統的平衡壓力為104.67kPa;在同樣的情況下,若放入NHI(s),則量得的平衡壓力為18.846kPa,試求固態NHC1和固態NHI的混合物在340℃時的平衡壓力。假設HI不分解,且此二鹽類不形成固溶體。
解:PNH3PHCt=(104.67/2)2kPa2=2739kPa2
PNH, Pm =(18.846/2)2kPa2=88.79kPa2
PNH =PHC +PH
以上三式聯立解:P=1.68kPa,P=51.8kPa
于是P=PNH +PHc +Pm =2(PHC+ Pm)=106. 96 kPa
5-29已知25℃水溶液中甲酸HC00H和乙酸HAc的標準離解常數K分別為1.82×10和1.74×10。求下列溶液中氫離子的質量摩爾濃度b(H)
(1)b=1mol·kg的甲酸水溶液;
(2)b=1mol·kg的乙酸水溶液;
(3)質量摩爾濃度均為b=1mo1·kg的甲酸和乙酸混合溶液。計算結果說明什么。
解:(1)b=1mol·kg的甲酸水溶液,高解平衡為
HCOOH=HCOO+H
1molkg'-xX
X
(x/b°)2
Kθ=1.82×10-=≈(x/b°)2
(Imol·kg-'-x)/b°
x/b°≈√1.82×10-=1.34×10-2
x=1.34×10-2mol·kg-=b(H*)
(2)b=1mol·kg"的乙酸水溶液;
HAc= Ac + H*
1mol·kg'-x(x/b°)2
K°=1.74×10-5=(Imol·kg-'-x)/b°
= (x/b°)2
x/b°=√17.4×10-6=4.17×10-3
x=4.17×10-3mol·kg-=b(H*)
(3)質量摩爾濃度均為 b=lmol·kg"的甲酸和乙酸混合溶液:
HCOOH =HCOO+H*(1)
1mol · kg'-xx+y
HAc= Ac+H*(2)
1 mol·kg'-yy
K =1.82×10+=(x/b°){(x+ y)/b°)
(Imol·kg'-x)/b°
(y/b°){(x+y)/b°)
(Imol·kg'-y)/b°
因為 x<<Imol·kg-', y<x<<Imol·kg-',故
(Imol·kg-'-x)/b°=1, (Imol-kg-'-y)/b°=1
x+y(a)
K = 1.74×105(b)
于是有
1.82x10= (x/b°){(x+y)/b°)
1.74×10* =(y/b°){(x+y)/b°)(d)
聯立上兩式,解得y=1.23×10-mol·kg-', x=1.289×10-3mol·kg-
所以 b(H")=x+y=(1.289x10-2+1.23x10-)mol-kg-=1.412x10-2mol-kg-1
(c)
5-30(1)應用路易斯-蘭德爾規則及逸因子圖,求 250℃、20.265MPa 下,合成甲醇反
應的 K;CO (g) +2H2 (g)=CH,OH (g)
(2)已知 250℃ 時上述反應的 △,G°=25.899kJ-mol',求此反應的K°;
(3)化學計量比的原料氣,在上述條件下達到平衡時,求混合物中甲醇的摩爾分數。
解:(1)CO 的對比參數為:
T,=TIT=523.15/132.92=3.94p,=20.265/3.499=5.79
查得Фсо=1.09
H2的對比參數為:
T,=T I(T+8K)=523.15/(33.25+8)=12.7
p,=p/(p, +0.8106MPa)=20.265/(1.297+0.8106)=9.62
查得Фн, =1.08
CH.OH(g)的對比參數為:
T,=TIT=523.15/512.58=1.02p,=20.265/8.10=2.50 查得
Фсн,он = 0.38
K, = Фсн,он (Фсо-Ф,)=0.38/(1.09x1.082) = 0.299
(2) In K° =-Δ,G (RT) =-25899/(8.314x523.15) =-5.9545
K°=2.59x10-3
(3)
初始物質的量1mol
平衡物質的量 (1-x) mol(2-x) mol
CO (g) + 2Hz (g)= CHOH (g)
2 mol0
x molna= (3-2x) mol
-2p
-2-2 6
用累試法求上述方程的近似根。因0<x<1,故可從 0.5 試起,結果可得
x=0.9023
所以y(甲醇)=x/(3-2x) =0.755
第六章 相平衡
6-1 指出下列平衡系統中的組分數 C,相數 P及自由度數 F
(1)I2(s)與其蒸氣成平衡;
(2)CaCO,(s)與其分解產物Ca0 (s)和COz(g)成平衡;
(3)NH.HS(s)放入一抽空的容器中,并與其分解產物 NHs(g)和 H;S (g)成平衡;
(4)取任意量的 NH,(g)和H2S (g)與NH.HS(s)成平衡;
(5) I:作為溶質在兩不相互溶液體 H20 和 CC1.中達到分配平衡(凝聚系統)。
解:(1) S-R-R'=1-0-0=1; P=2; F=C-P+2=1
(2) S-R-R'=3-1-0=2; P=3; F=C-P+2=1
(3) S-R-R'=3-1-1=1; P=2; F=C-P+2=1
(4) S-R-R'=3-1-0=2; P=2; F=C-P+2=2
(5) S-R-R'=3-0-0=3; P=2; F=C-P+1=2
6-2 已知液體甲苯(A)和液體苯(B)在90℃時的飽和蒸氣壓分別為p =54.22kPa和p =136.12kPa.兩者可形成理想液態混合物。今有系統組成為xgg=0.3的甲苯-苯混合物 5mol,在90℃下成氣-液兩相平衡,若氣相組成為ys=0.4556,求: (1)平衡時液相組成xg及系統的壓力 p;(2)平衡時氣、液兩相的物質的量 n(g),n(1).
解:(1)理想液態混合物,A、B 均適用拉烏爾定律,故有
p= px+ Pn = p(1-xn)+pix=54.22kPa(1-xg)+136.12kPaxg(1)
yg=0.4556= pn/p= pixg/p=136.12kPaxxg/p(2)
由式(1)及式(2)得
p=54.22kPa(1-xg)+136.12kPaxg(3)
0.4556 =136.12kPaxxg/p(4)
聯立式(3)與式(4),解 得p= 74.70kPa, xg = 0.2500
(2)根據杠桿規則
π)0456-0.00
×5mol = 3.784mol
n(g) = n-n(l) = (5-3.784)mol = 1.216mol
6-2 單組分系統硫的相圖示意如下.
試用相律分析相圖中各點、線、面的相平衡關系及自由度數
解:對于單組分系統,根據相律
F=C-P+2=3-P
若 P=1,則 F=2,單相在圖上表現為面,共有四個單相區,如
圖所示。
若 P=2,則 F=1,兩相平衡共存在圖上表現為線,稱為兩相線,
共有 6 條兩相線,即:ax 線表示正交硫與硫蒸氣平衡共存;yb 線
表示正交硫與液體硫平衡共存;zc 線表示液體硫與硫蒸氣平衡共
存;xy 線表示正交硫與單斜硫平衡共存;xz 線表示單斜硫與硫蒸氣
平衡共存;zy 線表示單斜硫與液體硫平衡共存。還有三條兩相亞穩
態平衡線: 0x線是 ax線的延長線,表示正交硫與硫蒸氣平衡兩相
亞穩態共存;Oy 線是 yb 線的延長線,表示正交硫與液體硫兩相亞正交碗
液體硫
單斜斑
膠蒸氣
穩態平衡共存;0z線是zc線的延長線,表示液體硫與硫蒸氣兩相亞穩態平衡共存;
若P=3,則F=0,三相平衡共存在圖表現為點,稱為三相點,共有4個三相點,即:x
點表示正交硫、單斜硫與硫蒸氣平衡共存;z點表示液體硫、單斜硫與硫蒸氣平衡共存;y點
表示正交硫、單斜硫與液體硫平衡共存;0點表示正交硫、液體硫與硫蒸氣平衡共存,不過
0點平衡是不穩定平衡,會自發轉變為穩定相一單斜硫
6-4已知甲苯、苯在90℃下純液體的飽和蒸氣壓分別為54.22kPa和136.12kPa。兩者
可形成理想液態混合物。
取200.0g甲苯和200.0g苯置于帶活塞的導熱容器中,始態為一定壓力下90℃的液態
混合物。在恒溫90℃下逐漸降低壓力,問:(1)壓力降到多少時,開始產生氣相,此氣相
的組成如何?(2)壓力降到多少時,液相開始消失,最后一滴液相的組成如何?(3)壓力
為92.00kPa時,系統內氣、液兩相平衡,兩相組成如何?兩相的物質的量各多少?
解:(1)與開始產生氣相平衡的液相,其組成同原始液態混合物,所以氣相的壓力為
200/78200/92
p=P苯x苯+P甲苯x甲苯=136.12×+54.22×
kPa
200/78+200/92200/78+200/92
=98.54kPa
氣相組成為y苯=P苯x苯P=136.12x
200/78
÷98.54=0.7476
200/78+200/92
(2)與最后一滴液相平衡的氣相,其組成同原始液態混合物
y苯=p苯x苯/p;p=P甲苯+(P苯-P甲苯)x苯
上兩式聯立解得:P甲苯y苯
X苯P苯-(p苯-P甲苯)y苯
200/78
54.22×200/78+200/92=0.3197
200/78
136.12-(136.12-54.22)×200/78+200/92
P=P甲+(P-P甲)x=[54.22+(136.12-54.22)0.3197]kPa=80.40kPa
(3)p=P甲苯+(P苯=P甲苯)x
92.00-54.22
X苯==0.4613
136.12-54.22
y=Px/p=136.12×0.4613/92.00=0.625
原始液態混合物的組成為
200/78=0.541
200/78+200/92
n0.541-0.4613
n0.6825-0.541聯立解得:n=1.709mol,n=3.022mol
200200
ng+n=7892
6-525C丙醇(A)-水(B)系統氣-液兩相平衡時兩組分蒸氣分壓與液相組成的關系如
下:X80
0.1
0.2
0.4
0.6
0.8
0.95
0.98
1
pA/kPa2.902.592.372.071.891.811.440.670
p/kPa 01.08
1.792.652.892.913.093.133.17
(1)畫出完整的壓力-組成圖(包括蒸氣分壓及總壓,液相線及氣相線);
(2)組成為Xa。=0.3的系統在平衡壓力p=4.16kPa下,氣-液兩相平衡,求平衡時氣相組成y及液相組成xn?
(3)上述系統5mol,在p=4.16kPa下達到平衡時,氣相、液相的物質的量各為多少?
(4)上述系統10kg,在p=4.16kPa下達到平衡時,氣相、液相的質量各為多少?
解:(1)由題給數據計算出對應液相組成的氣相總壓P=PA+PB及氣相組成yB=PBP計算結果列表如下:
XB0
0.1
0.2
0.4
0.6
0.8
0.95
0.981
p/kPa2.903.674.164.724.784.724.533.803.17
yB0
0.294
0.4300.5610.6050.6160.6820.8241
根據題給的及上述的數據,畫出完整的壓力-組成圖,如下圖所示
(2)從圖可以查出ya=0.429,x=0.2
(3)0.3-0.2
n.=5×mol=2.18mol
0.429-0.2t=25℃
5.0
4.0
3.0
2.0-
1.0
AXB
B
n =(5-2.18)mol =2.82mol
nA(g)=n (1-y)=2.18(1-0.429)mol=1.24mol
n(g)=ng yB =2.18×0.429mol=0.94mol
(4)M=60.096, M=18.015, y=0.429, XB=0.2
氣相與液相的平均摩爾質量分別為
M=∑yBMB=0.571×60.096+0.429×18.015
=42.043
M1=∑xBM8=0.8×60.096+0.2×18.015=51.680
m+m1=10kg
m(0.429-0.3)=(0.3-02)
M
上兩式聯立可得
M(0.3-02)
m,x(10kg-m)=0.631(10kg-m2)
M:(0.429-0.3)
m=3.87kg,m =10kg-m=6.13kg
6-6101.325kPa下水(A)-醋酸(B)系統的氣-液平衡數據如下
t/℃100
102.1
104.4
107.5
113.8
118.1
XB0
0.300
0.500
0.700
0.900
1.000
yn0
0.185
0.374
0.575
0.833
1.000
(1)畫出氣-液平衡的溫度-組成圖;(2)從圖上找出組成為x=0.800的液相的泡點;
(3)從圖上找出組成為y=0.800的氣相的露點;(4)105.0℃時氣-液平衡兩相組成是多
少?
(5)9kg水與30kg醋酸組成的系統在105.0℃達到平衡時,氣、液兩相的質量各為多少?
解:(1)根據題給的數據,畫出在101.325kPa下水(A)-醋酸(B)系統氣-液平衡的
溫度-組成圖,如下圖所示。
120p=101.325kPa
116112.8
112110.2
108g+1
104
1000.2
0.4
0.6
0.8
AXn
B
(2)由圖查得xm=0.800的液相的泡點為110.2℃.
(3)由圖查得y=0.800的液相的露點為112.8℃.
(4)由圖查得105.0℃時氣-液平衡兩相的組成為x=0.544,y=0.417.
(5)M=60.052, M-18.015, y=0.417, x=544
系統的總組成30×103/60.052
==0.500
30×103/60.052+9×103/18.015
系統總量n=(30×10/60.052+9x10/18.015)mo1=999.15mo1
根據杠桿規則n1={999.15×(0.500-0.417)/(0.544-0.417)}mol=653mol m1 =nM =653×(0.544×60.052+0.456×18.015)×103kg=26.69kgm=(39-26.69)kg =12.31kg
6-7已知水-苯酚系統在30℃液-液平衡時共軛溶液的組成w(苯酚)為:L(苯酚溶于
水),8.75%;L(水溶于苯酚),69.9%問:(1)在30℃、100g苯酚和200g水形成的系
統達到液-液平衡時,兩液相的質量各為多少?(2)在上述系統中再加入100g苯酚,又達
到相平衡時,兩液相的質量各為多少?
解(1)系統總組成w=100/(100+200)=33.3%
根據杠桿規則:69.9-33.3
m(L1)=300xg=179.6g, m(L2)=300g-179.6g=120.4g
69.9-8.75
(2)系統總組成苯酚=200/(200+200)=50%
根據杠桿規則:69.9-50
m(L1)=300xg=130.2g, m(L2)=400g-130.2g=269.8g
69.9-8.75
6-8水-異丁醇系統液相部分互溶。在101.325kPa下,系統的共沸點為89.7℃。氣(G)液(L1)、液(L:)三相平衡時的組成w(異丁醇)依次為:70%、8.7%、85.0%。今由350g水和150g異丁醇形成的系統在標準壓力下由室溫加熱,問:(1)溫度剛要達到共沸點時系統處于相平衡時存在那些相?其質量各為多少?(2)當溫度由共沸點剛有上升趨勢時,系統處于相平衡時存在那些相?其質量各為多少?
解:系統總組成為:150/(150+350)=30%
(1)存在液(L:)、液(L)二相平衡,根據杠桿規則,得
85.0-30.0
m(L1)=500×g=360g,
m(L2)=500g-360g=140g
85.0-8.7
(2)存在液(L)、液(L:)二相平衡,根據杠桿規則,得
30.0-8.7
m(G)=500xg=174g.
m(L2)=500g-174g=326g
70.0-8.7
6-9恒壓下二組分液態部分互溶系統氣-液平衡的溫度-組成圖如附圖(見教材p295),指出四個區域內平衡的相。
解:四個區域內平衡的相如圖中標注p=常數
g+1
AB
6-10為了將含非揮發性雜質的甲苯提純,在86.0kPa壓力下用水蒸氣蒸餾。已知:在此壓力下該系統的共沸點為80℃,80℃時水的飽和蒸氣壓為47.3kPa。試求:(1)氣相的組成(含甲苯的摩爾分數);(2)欲蒸出100kg純甲苯,需要消耗蒸氣多少?
解:(1)y=p/p=(86.0-47.3)/86.0=0.450
(2)0.550 m 118.015kgm水=23.9kg
0.450100×103/92.140
6-11液體H:0(A)、CC1:(B)的飽和蒸氣壓與溫度的關系如下:
t/℃40
50
60
70
80
90
pA/kPa7.38
12.33
19.92
31.16
47.34
70.10
PB/kPa28.8
42.3
60.1
82.9
112.4
149.6
兩液體成完全不互溶系統。(1)繪出H:0-CC1系統氣、液、液三相平衡時氣相中H:O、CC1
的蒸氣分壓及總壓對溫度的關系曲線;(2)從圖中找出系統在外壓101.325kPa下的共沸點;(3)某組成為y(含CC1的摩爾分數)的H:0-CC1氣體混合物在101.325kPa下泠卻到80℃時,開始凝結出液體水,求此混合氣體的組成;(4)上述氣體混合物繼續冷卻至70℃時,氣相組成如何?(5)上述氣體混合物冷卻到多少度時,CC1:也凝結成液體,此時氣相組成如何?
解:(1)由題給數據計算出不同溫度下的總壓p=p+p,繪出蒸氣壓對溫度的關系曲線如下圖:20
1.6
1.2
1.0
0.8
0.4
04050
60
70
80
90
c
(2)由圖查得共沸點為66.75℃.
(3)開始凝結出水,表明p=47.34kPa,所以混合氣體的組成為
yB=PBp=(p-PA)/p=(101.325-47.34)/101.325=0.533
(4)70℃時,p=31.16kPa,所以
y=Pu p=(p-pA)/p=(101.325-31.16)/101.325=0.692
(5)根據題意,氣、液、液三相平衡共存,惟有在共沸點下,所以1=66.75℃。此時氣相組成為:yB=PB / p=74.27/101.325=0.733
6-12A-B二組分液態部分互溶系統的液-固平衡相圖如附圖(見教材P296),試指出各個相區的相平衡關系,各條線所代表的意義,以及三相線所代表的相平衡關系
解:該圖各個相區的相平衡關系如下圖所標注。
mb線表示A(s)與L兩相平衡共存;bd線表示B(s)與L1兩相平衡共存;dLe線表示L與L兩液相平衡共存;ef線表示B(s)與L兩相平衡共存。有兩條三相線,即:abc線表示A(s).B(s)及液相L三相平衡共存,def線表示B(s)、液相L及液相L三相平衡共存。有三個三相點即b、d、e點
LL
S
L+L2+S
L,dS
mLAL,+B(s)
aC
bA(s)+B(s)
A
B
AB
題6題6.13附圖
題6.12
6-13固態完全互溶、具有最高熔點的A-B二組分凝聚系統相圖如附圖(見教材p297)指出各相區的相平衡關系、各條線的意義,并繪出狀態點為a、b的樣品的冷卻曲線。
解:各相區的相平關系及狀態點為a、b的樣品的冷卻曲線如圖所標注。HN那條線為液相線(液態熔體與固態熔體平衡線),而下方那條線為固相線(固熔體與液體熔體平衡線)同理,NO那條線為液相線(液態熔體與固態熔體平衡線),而下方那條線為固相線(固熔體與液體熔體平衡線)
6-14低溫時固態部分互溶、高溫時固態完全互溶且具有最低熔點的A-B二組分凝聚系統相圖如附圖(見教材p385).指出各相區的相平衡關系、各條線代表意義
解:各相區的相平衡關系如圖所注。HIK線是固熔體S1與固熔體S2的兩相平衡共存線,POQ那條線為液相線(液態熔體與固態熔體平衡線),而下方那條線為固相線(固熔體與液體熔體平衡線)Q
L
L+S
Pd
S<8
eBB
S+S2a
Hgw(Cd)
Cd
HK
B題6.15附圖(示意圖)
題6.14附圖
6-15二元系統Hg-Cd相圖示意如附圖(見教材p297)。指出各個相區的穩定相三相線上的相平衡關系。
解:各個相區的穩定相如圖中標注。兩條三相線上的相平衡關系如下
abc線:L=a+B; def線:L=B+y(a,B,Y為不同組成的固溶體)6-16某A-B二組分聚系統相圖如附圖(見教材p297).(1)指出各相區穩定存在的相;(2)指出圖中的三相線。三相線上哪幾個相成平衡?三者之間的相平衡關系如何?(3)繪出圖中狀態點a、b、c三個樣品的冷卻曲線,并注明各階段時的相變化
解:(1)各相區穩定存在的相如圖所注
abedL
L+2
MB
L+L
L+Yb3
9
e9
a2
aa+L
+B
a+Y6
a4b4a+β
ATV
dB
A
B
WB
題6-16附圖題6.17附圖
(2)該圖上有兩條三相線,即efg線是α固熔體與y固熔體和液相L相平衡,hij線是液相L與y固熔體和β固熔體相平衡
(3)圖中狀態點a、b、c三個樣品的冷卻曲線如圖右所示,a-al,組成為a的液態溶液降溫,達到al點時開始析出y固熔體,進入兩相平衡區,繼續冷卻達到a2時,開始析出第三相α固熔體,成三相平衡,直至液體全部凝結成α固熔體與y固熔體后,即自a2后繼續冷卻進入α固熔體與y固熔體平衡區;組成為b的液態溶液降溫,達到bl點時開始析出y固熔體和β固熔體,成三相平衡,繼續冷卻β固熔體消失,進入液體1和y固熔體,當泠卻達到b3時,直至液體消失,然后進入y固熔體單相區;組成為c的液態溶液降溫,達到cl點時開始析出β固熔體,進入兩相平衡區,繼續冷卻達到c2時,開始析出第三相y固熔體,成三相平衡,此后進入β固熔體與y固熔體兩相平衡區
6-17某A-B二組分聚系統相圖如附圖(見p297).指出各相區的穩定相,三相線上的相平衡關系
解:各相區的穩定相如6-17圖中所標,a,β為不同組成的、固溶體。兩條三相線上的相平衡關系為
abc線:L=a+B:efg線:L1+a=L
6-18利用下列數據,粗略繪出Mg-Cu二組分凝聚系統相圖,并標出各相區的穩定相Mg與Cu的熔點分別為
648℃、1085℃.兩者可形成1200
兩種穩定化合物,MgCu,
MgCu2,其熔點依次為580℃、L+Cu(s)
1000L
800℃。兩種金屬與兩種化合
物四者之間形成三種低共熔LMgCu2(s)
混合物。低共熔混合物的組成800L+Mg2Cu(s)
(含Cu%(質量))及低共熔
點對應為:Cu:35%,380℃;600
Cu:66%,560C;Cu:90.6%,L+Mg(s)
680℃。
解:由題給的數據,繪出400
MgCu2(s)
Mg-Cu二組分凝聚系統相圖如+
右圖所示。各相區的穩定相如200
Mg2Cu(s)+Mg(s)
Mg2Cu(s)
CuMgCu:
Mg:Cu
Mg
-Wt% Mg
圖所示。
6-19繪出生成不穩定化合物系統液-固平衡相圖(見p298)中狀態點為a、b、c、d、e、f、g的樣品的泠卻曲線。
解:根據題意,作出各條泠卻戰如
Cu(s)+MgCu2(s)
AC
B
WB
題6.19附圖
6-20A-B二組分凝聚系統相圖如附圖(見教材p298)。指出各個相區的穩定相,三相線上的相平衡關系。
解:各個相區的穩定相如圖中標注。三相線上的相平衡關系如下:
abc線:L=A(s)+C1(s); def線: L=C1(s)+C2(s)
ghi線:L=C2(s)+B(s)
LL+B(s)
L+
L+C2(s)
dL+C(s)
B
LCC(s)C2(s)C(s)+
Ca()B(s)
A(s)+C,(s)a+C
(s)
AC
C2B
A
B
WBWB
題6.20附圖題6.21附圖
6-21某A-B二組分聚系統相圖如附圖(見教材p298).標出各個相區的穩定相,并指出圖中三相線上的相平衡關系。
解:各相區的穩定相如圖中所注。該相圖有兩條三相線,即abc線和def線,abc線代表L+aC(s)三相平衡,def線代表L+β=C(s)三相平衡
6-22指出附圖(教材p298)中二元凝聚系統相圖如內各相區的穩定相,并指出三相線及三相平衡關系。
解:各相區的穩定相如圖所注:C=C1(s),C=C2(s),B=B(s)。該相圖有三條三相線,即EFG線、HIJ線及NOP線:EFG線表示L+a-C1(s)三相平衡,HIJ線表示L+C(s)=C2(s)三相平衡,NOP線表示L+B(s)=C2(s)三相平衡。
LL+CS
L+BLB()
L+CtN)
PL
L+C2L+C)
C(s)
HC2(s)+(s)
L.c.C:(s)
w aa+C(S)
F
a+C1+C2C2+B
A
C
C2B
AC
C
B
圖6-22題6.23附圖
6-23指出附圖(教材p387)中二元凝聚系統相圖如內各相區的穩定相,并指出三相線及三相平衡關系。
解:各相區的穩定相如圖所注:C1=C1(s),C2=C2(s),B=B(s).該相圖有三條三相線,即abc線、def線及ghi線:abc線表示L+a=C1(s)三相平衡,def線表示L+C2(s)=C1(s)三相平衡,ghi線表示L+B(s)=C2(s)三相平衡
6-2425℃時,苯-水-乙醇系統的相互溶解度數據(%(質量))如下:
苯0.1
0.4
1.3
4.4
9.2
12.8
17.520.030.0
水80.0
70.060.050.040.035.030.027.720.5
乙醇19.929.638.745.650.852.252.552.349.5
苯40.0
50.053.060.070.080.090.095.0
水15.2
11.09.87.5
4.6
2.3
0.8
0.2
乙醇44.839.037.232.5225.417.79.24.8
(1)繪出三組分液-液平衡相圖;(2)在1kg質量比為42:52的苯與水的混合液(兩相)中加入多少克的純乙醇才能使系統成為單一液相,此時溶液組成如何?(3)為了萃取乙醇,往1kg含苯60%、乙醇40%(質量)的溶液中加入1kg水,此時系統分成兩層。上層的組成為:苯95.7%,水0.2%,乙醇4.1%.問水層中能萃取出乙醇多少?萃取效率(已萃取出的乙醇占乙醇的總量的百分數)多大?
解:(1)由題給的數據,在等邊三角形坐標紙上,繪出苯-水-乙醇三組分系統液-液平衡相圖,如下圖所示。(2)在苯-水坐標上找出苯與水的質量
C HOH比為42:52的D點,將CD聯成直線與曲線
C相交于E點在1kg質量比為42:52的苯與
水的混合液中加入純乙醇,溶液的總組成沿
著DC線變化,當加到E點時,系統開始澄清
成為一相。
E點的組成為:苯19.6%,乙醇52.4%,
下層水28.0%
上層N
所以m=24×1kg-1.101kg
CHeD
HO
(3)因1kg含乙醇40%,苯60%的溶液
中乙醇量為0.4kg,苯量為0.6kg,加入1kg
圖6-21水后形成的系統總量為2kg,故系統的總組
圖6.24
成為(乙醇20%,苯30%,水50%),在圖中為N點,此時系統分為共軛的液層:已知上層(苯層)的組成為{乙醇4.1%,苯95.7%,水0.2%},以F點表示;將FN聯一直線與曲線交于G點,此點的組成即下層(水層)的組成為(乙醇27.2%,苯0.3%,水72.5%)。根據杠桿規則:m下層(30-0.3)=(2kg-m下)(95.7-30):
m下=1.38kg
下層(水層)中含乙醇的量m乙=1.38kgx27.2%=0.375kg
0.375
萃取效率=×100%=93.8%
0.4
增加題在325C時,Hg的蒸氣壓為55.49kPa,同溫度下Tl-Hg合金中Hg的分壓及摩爾分數如下:
XHg1.000
0.957
0.915
0.836
0.664
0.497
PHg/kPa55.49
53.00
50.00
44.55
33.40
24.03
求對應于各濃度時汞的活度及活度因子(系數)
解:解:選擇純Hg在325℃時的狀態PH=55.49kPa作為標準態最為合適,活度及活度系數就可用下兩式求出,結果列在下表。aHg=PHg IPHg, YHg =aHg IxH
XHg1.000
0.957
0.915
0.836
0.664
0.497
PHg/kPa55.49
53.00
50.00
44.55
33.40
24.03
aHg1
0.9551
0.9011
0.8028
0.6019
0.4331
YHg1
0.9980
0.9848
0.9603
0.9065
0.8713
第七章電化學
7.1用鉑電極電解CuCl2溶液。通過的電流為20A,經過15min后問:(1)在陰極上能析出多少質量的Cu?(2)在的27℃,100kPa下陽極上能析出多少體積的的Cl2(g)?
解:電極反應為:陰極:Cu2++2e→Cu
陽極:2C-2e→Cl2(g)
則:z=2
根據:Q=nzF=Itn(Cu)==
20×15=9.326×102mol
2×96500
因此:m(Cu)=n(Cu)×M(Cu)=9.326×102×63.546=5.927g
又因為:n(Cu)=n(Cl2)pV(Cl2)=n(Cl2)RT
因此:V(Cl,=n(ClRT
0.09326×8.314×300=2.326dm
100×10
7.2用Pb(s)電極電解PbNO3溶液。已知溶液濃度為1g水中含有PbNO
1.66×10g。通電一定時間后,測得與電解池串聯的銀庫侖計中有0.1658g的銀
沉積。陽極區的溶液質量為62.50g,其中含有PbNO31.151g,計算Pb2t的遷移數。
解法1:解該類問題主要依據電極區的物料守恒(溶液是電中性的)。顯然
陽極區溶液中Pb2的總量的改變如下:
11電解后
(Pb2+)=n電解前(Pb2+)+n電解(Pb2+)-n遷移(Pb2+)
則:n遷移(Pb2)=n
電解前(Pb2+)+n電解(Pb2+)-n電解后(Pb2+)n電解(Pb2)=n電解(Ag)=m(Ag)_0.1658=1.537×103mol
M(Ag) 107.9
(62.50-1.151 ×1.66×102
n電解前
)=6.150×103mol
331.2×
)1.151
=6.950×103mol
電解后331.2×
n(Pb2+)=6.150×103+1.537×103-6.950×103=7.358×104mol
2t(Pb2
過移
7.358×10
=0.479
n電解/2P6)1.537×10
解法2:解該類問題主要依據電極區的物料守恒(溶液是電中性的)。顯然
陽極區溶液中NO的總量的改變如下:
n電解后(NO,)=n電解前(NO)+n遷移(NO)則:n遷移(NO,)=n電解后(NO)-n電解前(NO)
1.151
n電解后(NO)=n(Pb2+)
=6.950×103mol
電解后2331.2×
n電解前(NO)=n
電解前(
Gpo)62.50-1.151 ×1.66×10
=6.150×10mol
331.2×
n(NO)=6.950×103-6.150×103=8.00×10mol
n(NO,)8.0×10
t(NO遷移
=0.521
1n電解1.537×10
則:t(Pb2+)=1-t(NO)=1-0.521=0.479
7.3用銀電極電解AgNO3溶液。通電一定時間后,測知在陰極上析出0.078g
的Ag,并知陽極區溶液中23.376g,其中含AgNO30.236g。已知通電前溶液濃度
為1kg水中溶有7.39g
AgNO3。求Ag*和NO,遷移數
解法1:解法1:解該類問題主要依據電極區的物料守恒(溶液是電中性的)。
顯然陽極區溶液中Ag的總量的改變如。
n電解后(Ag)=n電解前(Ag*)+n電解(Ag*)-n遷移(Ag*)
則:n遷移(Ag*)=n電解前(Ag*)+n電解(Ag*)-n電解后(Ag*)
m(Ag)_0.078
n電解Ag*)=-=7.229×10mol
M(Ag)107.9
23.376-0.236)×7.39×10
1n電解前(Ag')==1.007×10mol
169.87
0.236
n解后
(Ag')==1.389×103mol
169.87
n遷移Ag*)=1.007×103+7.229×104-1.389×103=3.403×10mol
n(Ag)
t(Ag遷程
3.403×10
=0.47
ni電解7.229×10
則:t(NO)=1-t(Ag*)=1-0.471=0.53
解法2:解該類問題主要依據電極區的物料守恒(溶液是電中性的)。顯然
陽極區溶液中NO,的總量的改變如下:
n電解后(NO3)=n電解前(NO3)+n遷移(NO3)
則:n移(NO)=n電解后(NO)-n電解(NO3)
0.236
nt電解后(NO3)=n電解后(Ag)==1.389×103mol
169.87
23.376-0.236)×7.39×10
n電解前(NO3)=n
電解前(Ag)==1.007×103mol
169.87
n(NO,)=1.389×103-1.007×103=3.820×103mol
Ag)=m(Ag)0.078
n電解=7.229×10mol
M(Ag)107.9
n
遷移(NO,)3.820×10
t(NO=0.53
電解7.229×10
則:t(Ag*)=1-t(NO,)=1-0.528=0.47
7.4在一個細管中,于0.3327mol-dm3的GdCl3溶液的上面放入0.073mol-dm
的LiCl溶液,使它們之間有一個明顯的界面。令5.594mA的電流直上而下通過
該管,界面不斷向下移動,并且一直是很清晰的。3976s以后,界面在管內向下
移動的距離相當于1.002cm3的溶液在管中所占的長度。計算在實驗溫度25℃下,
GdCl3溶液中的t(Gd)和t(CI)。
解:此為用界面移動法測量離子遷移數。
1.002cm3溶液中所含Gd的物質的量為:
n(Gd3)=cV=0.03327×1.002×103=3.3337×103mol
所以Gd和CI的的遷移數分別為:
Q(Ge")n(Ge")zF3.3337×10×3×96500
(Ge")==0.434
It5.594×10×3976
t(CI)=1-t(Gd)=1-0.434=0.566
7.5已知25℃時0.02mol-dm3KCl溶液的電導率為0.2768S-m。一電導池中
充以此溶液,在25℃時測得其電阻為453W。在同一電導池中裝入同樣體積的質
量濃度為0.555mol-dm3的CaCl2溶液,測得電阻為1050W。計算(1)電導池系
數;(2)CaCl2溶液的電導率;(3)CaCl2溶液的摩爾電導率。
解:(1)電導池系數為
Kc=kR=0.2768' 453=125.4 m'K=KG=K即K=KR
R
則:Kcell=0.2768×453=125.4m
(2)CaCl2溶液的電導率K
K=125.4=0.1994S-m
1050
(3)CaCl2溶液的摩爾電導率
K0.1194×110.983
An=0.02388S.m2.mol
C0.555×103
7.6.已知25C時A(NHCI)=0.012625Sm2mol,t(NH0.4907。試計
算A(NH)及A(C)
解:離子的無限稀釋電導率和電遷移數有以下關系
(NH
A(NH.CI)0.4907×0.012625
A(NH)6.195×10S.m2.mol
V.l
A(cr)=(CI A (NH.CI)(1-0.4907)×0.012625
=6.430×10S.m2.mol
V1
或A=vA+v
A(CI)=A(NHCl)-A(NH)=0.012625-6.195×103=6.430×103S-m2.mol
7.725C將電導率為0.14S-m的KC1溶液裝入一電導池中,測得其電阻為525W。在同一電導池中裝入0.1mol-dm3的NH3·H2O溶液,測得電阻為2030W。
利用表7.3.2中的數據計算NH3H2O的解離度a及解離常熟K。
解:查表知NH3H2O無限稀釋摩爾電導率為
A(NHHO)=A(NH)+A(OH)
=73.5×10+198×10=271.5×10S.m2.mol
A(NH,H2O)K(NH,H2O)
A(NH,HO)c(NH,HO)A(NH,HO)
KG(NHHO)(KCl)R(KCI
c(NH,HO)A(NH,HO)c(NH,HO)R(NH,HO)A(NH,·HO
0.141×525
0.1×1000×2030×271.5×10
=0.01344
c(NH=
(0H)
Kca2
0.013442×0.1
=1.834×10
c(NH,H,O(1-a)c
(1-0.01344)×1
7.825C時水的電導率為5.5×106S-m1,密度為997.0kg·m2。H2O中存在
下列平衡:H2OH+OH,計算此時H2O的摩爾電導率、解離度和H
的濃度。已知:A(H*)=349.65×10S-m2-mol1,A(OH)=198.0×104S-m2mol。解:A(H2O)=k(H2O)k(H2O)
c(H2O)p(H2O)IM(H2O)
5.5×106=9.93×10S.m2.mol
997.09×103/18
Am(H2O)Am(H2O)
4(H2O)A(H)+4(OH)
9.929×10-S.m2mol-=1.813×10
(3.49.65+198.0)×10S-m2mol
c(H*)= ca=p(H2O)/M(H2O)a=×1.813×10=1.004×10'mol-md-3
7.9已知25C時水的離子積K=1.008×10,NaOH、HCl和NaCl的A分
別等于0.024811S-m2mol1,0.042616S.m2-mol和0.0212545S.m2.mol。
(1)求25℃時純水的電導率;
(2)利用該純水配制AgBr飽和水溶液,測得溶液的電導率(溶液)=
1.664×10S-m,求AgBr(s)在純水中的溶解度
已知:A(Ag*)=61.9×104S.m2.mol,A(Br)=78.1×104S.m2.mol
解:(1)水的無限稀釋摩爾電導率為
A(HO)=A(HCI)+A(NaOH)-A(NaCl)
=0.042616+0.024811-0.012645=0.054777S.m2.mol
純水的電導率
K=
-()即:ca=Kc
Am(H2O)=(H2O)
C
(H2O)=KcA(H2O)
即有:=√1.008×104×1×103×0.054777=5.500×10S.m-
(2)K(溶液)=K(AgBr)+K(H2O)
即:(AgBr)=(溶液)-(H2O)
=1.664×105-5.500×106=1.114x105S.m
A(AgBr)≈A(AgBr)=A(Ag)+A(Br)
=61.9×102+78.1×10=1.40×102S-m2mol
K(AgBr)r(AgBr)
1.114×10
Am(AgBr)=即
=7.957×10mol-m-3
CAm(AgBr)
1.40×10
7.10應用德拜-休克爾極限公式計算25℃時0.002mol-kgCaCl2溶液中y
(Ca2+)、y(CI)和y±。
解:離子強度
1=bn==[0.002×2+0.002×2×(-1)*]=0.006mol-kg*
根據:lgy=-Az2I:lgy,=-Az.|z|
即:1gy(Ca0:509 2 )2×√0.006=-01577 y Ca2=0.6995
lgy(C10.509 (-1)×√0.006=-0.03943 y Cl=0.9132
lgy=-Az.|z|√I=-0.509×2×|-1|√0.006 =-0.07885:y=0.8340
7.11現有25℃時,0.01mol-kgBaCl2溶液。計算溶液的離子強度I以及BaCl2
的平均離子活度因子y4和平均離子活度。
解:離子強度
1=b==[0.01×2+0.01×2×(-1)*]=0.03mol-kg"
根據:lgy=-Az.|z|√I=-0.509×2×|-1|×√0.03=-0.1763y_=0.6663b=(bb)=(0.01×0.022)=1.587×10mol·kg
a1=y=0.6663×1.587×10=0.01057
7.1225℃時碘酸鋇Ba(IO4)2在純水中的溶解度為5.46×10mol-dm3。假定可
以應用德拜-休克爾極限公式,試計算該鹽在0.01mol-dm3中CaCl2溶液中的溶
解度。
解:先利用25℃時碘酸鋇Ba(IO4)2在純水中的溶解度求該溫度下其溶度積。由
于是稀溶液可近似看作bB≈cB,因此,離子強度為
/=∑bz=[5.46×104x2+5.46x104x2x(-1)2]=1.638x104mol-kglgy=-Az.|z|√I=-0.509×2×|-1|×√1.638×103=-0.04120y=0.9095K_=a(Ba)a2(IO)=4y()=4×0.9095×5.46×10°=4.898×10
設在0.01mol-dm3中CaCl2溶液中Ba(IO4)2的溶解度為b,則
1=b=[0.01×2'+0.01×2x(-1)+6b]=3(0.01+b)mol-kglgy=-Az.|z.|√I=-0.509×2x|-1|x√3(0.01+b)
K,=(Ba )a (10,)=4() b-
4.898×10b4.966×10b
b4
整理得到
lgy=-1.7632×(0.01+4.966×10*)/y
采用迭代法求解該方程得=0.6563
所以在0.01mol-dm3中CaCl2溶液中Ba(IO4)2的溶解度為
b=-
4.898×10be
4.966×10*×1=7.566×10*mol-kg
40.6563
CBbB=7.566x10mol-dm3
7.13電PtH2(101.325kPa)HCl(0.10mol-kg)Hg2Cl2(s)lHg電
E與溫度T的關系為:
=0.0694+1.881×103-2.9×10*()
(1)寫出電池反應:
(2)計算25C時該反應的ArGm、ArSm、ArHm以及電池恒溫可逆放電時該
反應過程的Qr.m。
(3)若反應在電池外在同樣條件恒壓進行,計算系統與環境交換的熱。
解:(1)電池反應為
5H2(g)+5Hg2Cl2(s)=Hg(1)+HCl(aq)
(2)25C時
E=0.0694+1.881×103×298.15-2.9×10×(298.15)2=0.3724V
=1.881×103-2×2.9×10×298.15=1.517×10V-K-
因此,ArGm=-zEF=-1×96500×0.3724=-35.94 kJ-mol
A.S=zF=1×96500×1.517×10=14.64J·molK-
ArHm=AtGm +TArSm=-35.94+14.64×298.15×103=-31.57 kJ.molQr.m=TArSm=4.36 kJ-mol
(3)Qp.m=ArHm=-31.57 kJ.mol
7.1425C時,電池ZnlZnCl2(0.555 mol-kg)lAgCl(s)lAg的電動勢E=
1.015V。已知E(Zn2*Zn)=-0.7620V,E(CllAgClAg)=0.2222V,電池電
動勢的溫度系數為:=-4.02×10V.K-
(1)寫出電池反應;
(2)計算反應的標準平衡常數K°;
(3)計算電池反應的可逆熱Qrm;
(4)求溶液中ZnCl2的平均離子活度因子y
解:(1)電池反應為
Zn(s)+2AgCl(s)=Zn2++2Cl+2Ag(s)
(2) A.G=-RTIn K=-zEF
即:InKzEF2×[0.2222-(-0.7620)]×96500=76.63
RT8.314×298.15
K=1.90×1033
(3e-TA,5.-=2 ().
=2×96500×(-4.02×10)×298.15=-23.13kJmol
(4)E-P RT malZn"(Cr)-E)
8.314×298.15
1.015=0.2222-(-0.7620)-2×96500ln4y20.5555
7=0.5099
7.15甲烷燃燒過程可設計成燃料電池,當電解質微酸性溶液時,電極反應和
電池反應分別為:
陽極:CH4(g)+2H2O(1)=CO2(g)+8H*+8e
陰極:2O2(g)+8H+8e=2H2O(1)
電池反應:CH4(g)+2O2(g)=CO2(g)+2H2O(1)
已知,25℃時有關物質的標準摩爾生成吉布斯函數AG為:物質CH4(g)
CO2(g)
H2O(1)
AG/ kJmol-50.72
-394.359
-237.129
計算25℃時該電池的標準電動勢。
解:△,G=∑v△1G(B)
=AG(CO,g)+2AG(H2O 1)-AG(CH g)-2AG(O2g)
=-394.359+2×(-237.129)-(-50.72)
=-817.897kJ-mol
因為:AG=-zEF
EAGm_817.897×103=1.0595V
zF 8×96500
7.16寫出下列各電池的電池反應。應用表7.7.1的數據計算25C時各電池的
電動勢、各電池反應的摩爾Gibbs函數變及標準平衡常數,并指明的電池反應能
否自發進行。
(1)PtlH2 (100kPa)IHCl (a=0.8) ICl2 (100kPa)Pt(2)Znl Zn Cl2 (a=0.6)lAgCl (s) lAg
(3)CdlCd2+(a=0.01) Cl(a=0.5)1Cl2(100kPa)IPt解:(1)電池反應:H2(g)+Cl2(g)=2HC
E=Eo-KI Ina2(HCl=135798.314×29.5I08=13636V
2×96500
A.G=-zEF=-2×1.3636×96500=-263.17kJmol
A,G=-RT In K=-zEF
InKzEF2x[1.3579-0]×96500=105.726
RT8.314×298.15
K=8.24×1045
A.G=-zEF<0,故件下反自行。
(2)電池反應:Zn(s)+2AgCl(s)=ZnCl2+2Ag(s)
E=E-Ina(ZnCl2)=(0.22216+0.7620)-
8.314×298.15In0.6=0.9907V
2×96500
AG=-zEF=-2×0.9907×96500=-191.20kJ.mol
A.G=-RT In K=-zEF
In Ke=zEF2×[0.22213-(-0.7620)]×96500=76.626
RT8.314×298.15
K=1.898×1033
AG<0故件下反自行。
(3)電池反應:Cd(s)+Cl2(g)=Cd2++2ClE-Eo-RI(er)
8.314×298.15
=(1.3579+0.4032)-lnO.01×(0.5)2=1.8381V
2×96500
AG=-zEF=-2×1.8381×96500=-354.75kJ-mol
A.G=-RTIn K=-zEF
In KzEF2x[1.3579(-0.4032)]×96500=137.119
RT8.314×298.15
K=3.55×1059
A.G<0故件下反自行。
7.17應用表7.4.1的數據計算下列電池在25℃時的電動勢。
CulCuSO4 (bi=0.01mol-kg') ICuSO4 (b2=0.1mol-kg') ICu
解:該電池為濃差電池,電池反應為
CuSO4 (b2=0.1mol-kg1)→ CuSO4 (b=0.01mol-kg1)
查表知,y±(CuSO4,bi=0.01mol-kgl)=0.41
+ (CuSO4, b2=0.1mol-kg) =0.16
Y+jb
=-RTn98.314x 298.15 0.41x 0.01
-= 0.01749V
2×965000.16×0.10
be
7.18 電池 PtlH2 (100kPa) IHCl (b=0.10 mol-kgl) ICl2 (100kPa) IPt 在 25℃
時電動勢為 1.4881V,試計算 HCI 溶液中 HCI 的平均離子活度因子。
解:該電池的電池反應為
H2 (g, 100kPa) +Cl2 (g, 100kPa)= 2HCl (b=0.10 mol-kg)
根據 Nernst 方程a (HCI)
E=E°-F[p(H)/p°][p(CI.)/p°]
=E-na(HCI)
1.4881=1.3579-8.314x298.15Ina (HCI)
a(HCI) = 6.29×10-3
2×96500
(HCI) = =() = (HC)=6.29x107 =0.79317.19 25℃時,實驗測定電池 PbPbSO4(s) IH2SO4(0.01 mol-kg1)IH2(g,
p9)IPt的電動勢為0.1705V。已知25℃時, A,G (H2SO4, aq)=A,G (SO2,
aq) =-744.53kJ-mol, Δ,G (PbSO4, s) = -813.0kJ-mol.
(1)寫出上述電池的電極反應和電池反應;
(2)求 25℃時的 Eθ(SO?IPbSO4IPb);
(3)計算 0.01 mol-kg' H2SO4溶液的 a4和 y±。
解: (1)上述電池的電極反應和電池反應如下
正極:2H*+2e=H2(g,po
負極:Pb(s)+SO?-2e=PbSO4(s)
電池反應:H2SO4(0.01 mol-kg')+Pb (s)=PbSO4(s)+H2(g,po)
(2) Δ,G = ΣνΔ,G (B)
= AG (PbSO,, s)+24,G (H, g)-4,G(HSO, aq)-A,G (Pb s)
=-813.0+0-(-744.53)-0
=-68.47kJ.mol-
因為: A.C=-2E°F=-2(E°(HH,Pt -E° SO|PbSO.|Pb)F
E°(90; |PbSo,Pb -6847x0-03548V
(3) E=-
0.17050.3548)42
a.(H2SO.)=8.369×10
b,(H,So.)= ())" = (0.02 x0.01)" = 1.5874x10'mol-kg"
a, (H,SO,)=.()
=y,=a,(H,5O,)-×8.3694 ×10=0.527
1.5874 ×10-2
7.20 濃差電池 Pb| PbSO4 (s) |CaSO4 (b1,y.1) | CaSO4 (b2, ys2) | PbSO4
(s) |Pb,其中 bi=0.2 mol-kg',y±.1=0.1;b2=0.02 mol-kg",y±.2=0.32,已知在
兩液體接界處 Cd2+離子的遷移數的平均值為 t(Cd2+)=0.37。
(1)寫出電池反應;
(2)計算 25°℃ 時液體接界電勢 E(液界)及電池電動勢 E:
解:電池反應CdSO4 (a±. 1) → CdSO4 (a±. 2)
由 7.7.6 式
Ε(液界)=(.-.)
4-012= 0.02 =0.322=64x10
()=(0.37-0.63x.34x23.805x0
電池電動勢
E = E(濃差液臥)--)-
=2x0.37x8.314x29810020.01083
7.21為了確定亞汞離子在水溶液中是以Hgt還是以Hg?形式存在,涉及了如
下電池HNO,0.1mol·dm
HNO,0.1mol·dm
硝酸汞假63hol·dm2.63mol · dm
Hg
測得在 18℃ 時的 E= 29 mV,求亞汞離子的形式。
解:設硝酸亞汞的存在形式為Hg?,則電池反應為
2NO; (a, (NO;)}+ Hg, (NO,), {a[Hg, (NO,),])→
2NO; {a, (NO;)}+Hg, (NO,), {a[Hg, (NO,),]}
電池電動勢為a(NO; )a,[Hg, (NO,),
E=-F(NO;)a, Hg, (NO,),
作為估算,可以取a,(NO;)=a,(NO;): a[Hg,(NO,),]
[Hg,(NO,)
a,[Hg, (NO,),]
c,[Hg,(NO,),]
Ea(NO;)a, [Hg, (NO,),]
a{ (NO;)a,[Hg, (NO,),
-8.314×291.150.263
=29mV
2×96500
所以硝酸亞汞的存在形式為Hg?*。
7.22 電池 Pt|H2 (g, 100kPa) | 待測 pH 的溶液 1l 1mol-dmKCI |Hg2Cl2 (s)
Hg,在 25℃時測得電池電動勢 E=0.664V,試計算待測溶液的 pH。
解:電極及電池反應為
陽極: H2 (g, 100kPa)-2e=2H
陰極: Hg2Cl2 (s) +2e=2Hg (1) +2Cl
電池反應:H2(g, 100kPa) +: Hg2Cl2(s)=2Hg(1)+2H++2Cr查表知(表 7.8.1),在所給條件下甘汞電極的電極電勢為0.2799 V,則:
-)
2=0.2799-na(H')
.6640.2799.4Ina (H')
a (H') = 3.21×107
pH=lga (H*) = Ig3.21x107 = 6.49
7.23在電池Pt|H2 (g, 100kPa) |HI溶液(a=1) |12 (s) |Pt中,進行如
下電池反應:
(1) H2 (g, 100kPa) +I2 (s)2HI (a=1)
(2) Hz (g. po) + (s)HI (aq,a=1)
應用表7.7.1 的數據計算兩個電池反應的E9、A,G和Ke.
解:(1)電池反應為 H2(g, 100kPa) +I2 (s)2HI (a=1)
時,電池反應處于標準態,即有:
Eθ = Εθ (Γ (a=1) |I2|Pt) - Eθ (H* (a=1) |H2 (g, 100kPa) |Pt)=0.5353V
= E (T溶液 (a=1) |I2 (s) |Pt)
Δ.G (1)=-zE°F=-2x0.5353x 96500 =-103.31kJ -mol"
AGm) = exp
K° (1)=exp(-= 1.26x1018
RT
(2)電動勢值不變,因為電動勢是電池的性質,與電池反應的寫法無關,
103310
8.314× 298.15
E°=0.5353V
Gibbs 自由能的變化值降低一半,因為反應進度都是 1 mol,但發生反應的
物質的量少了一半,即
Δ.G(2)=A.G() =-51.66 kJ- mol"
根據平衡常數與Gibbs自由能變化值的關系,
x°(2) =[x°]==[1.26x10"]=1.12x10°
上一篇:雙軸破碎機和圓盤破碎機的PK賽
下一篇:鍋爐煙氣除塵工藝









