題目：設AB是圓的直徑，過A，B分別作弦AC，BD相交于點E，證明：AE·AC+BE·BD＝                     分析：這類題通常與相似三角形相關，式子中出

題目：

設AB是圓的直徑，過A，B分別作弦AC，BD相交于點E，證明：AE·AC+BE·BD＝

分析：這類題通常與相似三角形相關，式子中出現的AE，BE提示我們過點E作EF⊥AB于F而構造相似三角形，如圖。

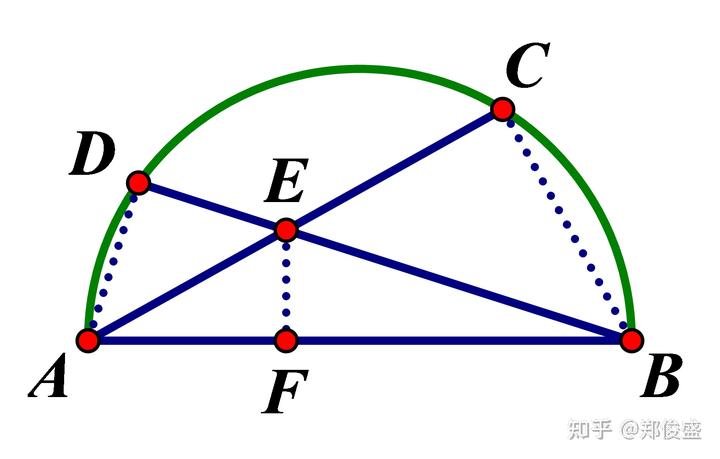
如此一來，因為∠ACB＝90°，∠AFE＝90°，∠BAC＝∠BAC；∠BDA＝90°，∠BFE＝90°，∠ABD＝∠ABD，所以

ΔACB∽ΔAFE，ΔBDA∽ΔBFE

所以

AB：AE＝AC：AF；AB：BE＝BD：BF

即

AE·AC＝AB·AF；BE·BD＝AB·BF

兩式相加，得

AE·AC+ BE·BD＝AB·AF+AB·BF＝AB(AF+BF)=AB·AB=